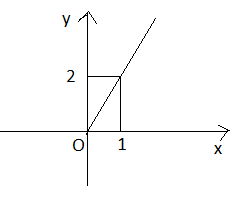Giải bài tập SBT Toán 10 Bài 2: Hàm số y = ax + b

Vẽ đồ thị của các hàm số sau và xét tính chẵn lẻ của chúng

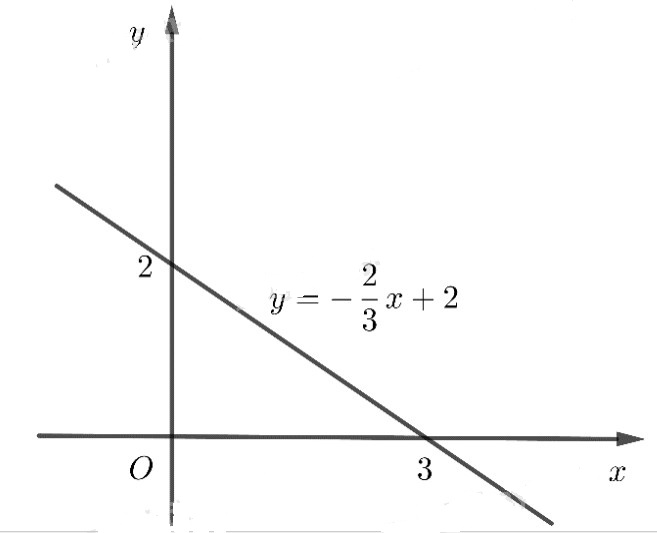
a) \(y = - \dfrac{2}{3}x + 2\)

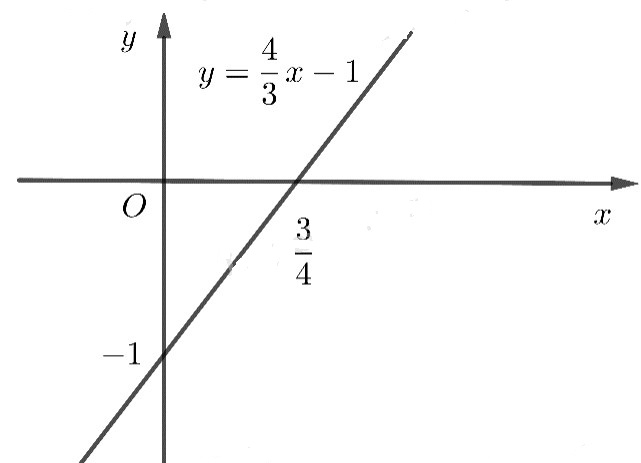
b) \(y = \dfrac{4}{3}x - 1\)

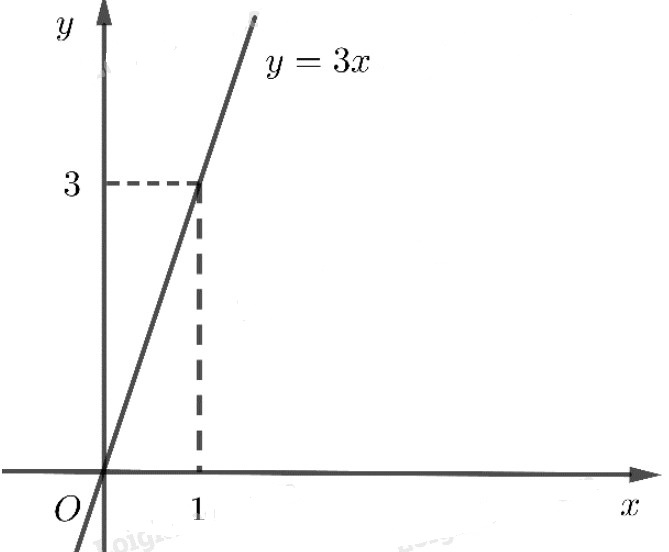
c) y = 3x

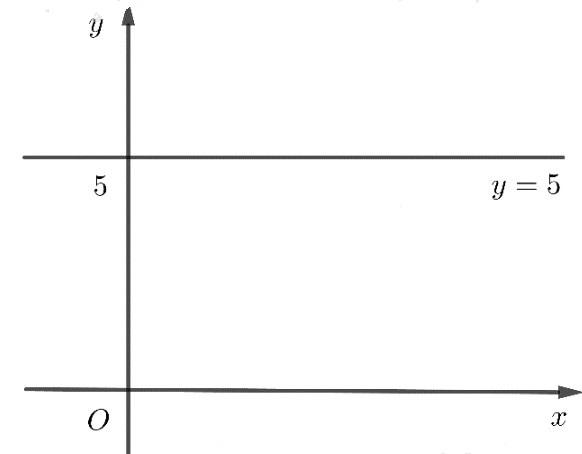
d) y = 5

Phương pháp giải

Cách vẽ đồ thị hàm số y = ax + b ( a ≠ 0).

Bước 1: Cho x = 0 thì y = b, ta được điểm P(0; b) thuộc trục Oy.

Cho y= 0 thì x= \(\frac{{ - b}}{a}\) , ta được điểm Q(\(\frac{{ - b}}{a}\);0) thuộc trục hoành Ox.

Bước 2: Vẽ đường thẳng đi qua hai điểm P và Q ta được đồ thị hàm số y = ax + b.

Hướng dẫn giải

a) Cho x = 0 thì y = 2, y = 0 thì x = 3 nên đồ thị đi qua hai điểm A(0;2) và B(3;0).

Hàm số không là hàm số chẵn, không là hàm số lẻ.

b) Cho x = 0 thì y = −1, y = 0 thì \(x = \frac{3}{4}\) nên đồ thị đi qua hai điểm A(0;−1) và \(B\left( {\frac{3}{4};0} \right)\)

Hàm số không là hàm số chẵn, không là hàm số lẻ.

c) Cho x = 0 thì y = 0, y = 3 thì x = 1 nên đồ thị đi qua hai điểm A(0;0) và B(1;3).

Hàm số là hàm số lẻ.

d) Cho x = 0 thì y = 5, x = 2 thì y = 5 nên đồ thị đi qua hai điểm A(0;5) và B(1;5).

Hàm số là hàm số chẵn.

Vẽ đồ thị hàm số

\(y = \left\{ \begin{array}{l}2x - 1,x \ge 1\\\dfrac{1}{2}x + 1,x < 1\end{array} \right.\)

Phương pháp giải

Cách vẽ đồ thị hàm số y = ax + b ( a ≠ 0).

Bước 1: Cho x = 0 thì y = b, ta được điểm P(0; b) thuộc trục Oy.

Cho y= 0 thì x= \(\frac{{ - b}}{a}\) , ta được điểm Q(\(\frac{{ - b}}{a}\);0) thuộc trục hoành Ox.

Bước 2: Vẽ đường thẳng đi qua hai điểm P và Q ta được đồ thị hàm số y = ax + b.

Hướng dẫn giải

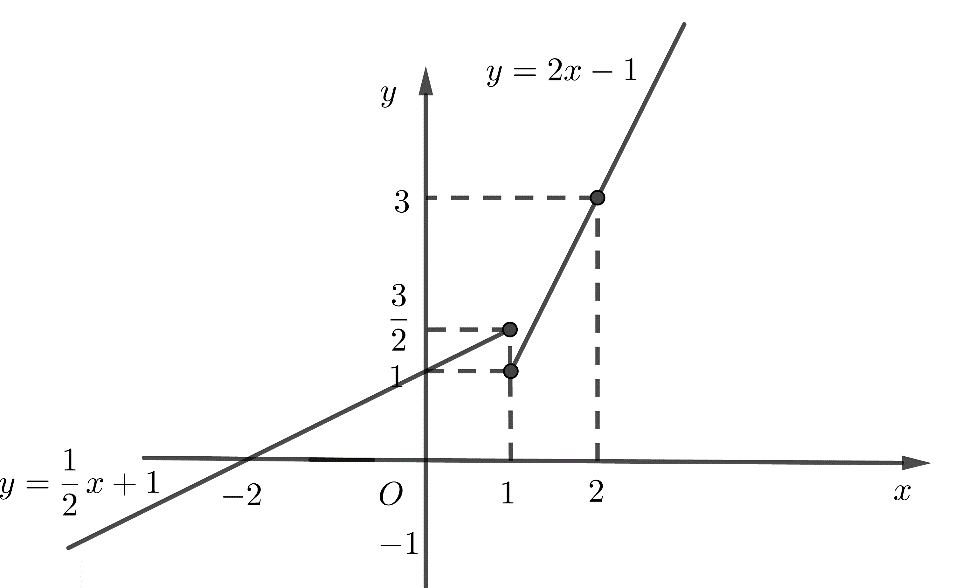
+) Vẽ đồ thị hàm số y = 2x - 1

Cho x = 1 thì y = 1 ta được điểm \(\left( {1;1} \right)\)

Cho x = 2 thì y = 3 ta được điểm \(\left( {2;3} \right)\)

Nối hai điểm trên kéo dài ta được đồ thị hàm số y = 2x - 1

Xóa phần đồ thị ở phía x < 1 đi.

+) Vẽ đồ thị hàm số \(y = \frac{1}{2}x + 1\)

Cho x = 0 thì y = 1 ta được điểm \(\left( {0;1} \right)\)

Cho x =  - 2 thì y = 0 ta được điểm \(\left( { - 2;0} \right)\)

Nối hai điểm trên kéo dài ta được đồ thị hàm số \(y = \frac{1}{2}x + 1\)

Xóa phần đồ thị ở phía \(x \ge 1\) đi.

+) Hợp hai phần đồ thị còn lại ta được đồ thị hàm số đã cho.

Điểm (1 ;1) thuộc đồ thị , điểm \((1;\dfrac{3}{2})\) không thuộc đồ thị.

Xác định các hệ số a và b để đồ thị của hàm số y = ax + b đi qua các điểm sau

a) \(A\left( {\frac{2}{3}; - 2} \right)\) và B(0;1)           

b) M(−1;−2) và N(99;−2)

c) P(4;2) và Q(1;1)

Phương pháp giải

Để xác định các hệ số a và b ta dựa vào tọa độ các điểm mà đồ thị đi qua, lập hệ phương trình có hai ẩn a và b.

Hướng dẫn giải

a) Vì đồ thị đi qua \(A\left( {\frac{2}{3}; - 2} \right)\) nên ta có phương trình \(a.\frac{2}{3} + b = - 2\)

Tương tự, dựa vào tọa độ của B(0;1) ta có 0+b = 1

Vậy, ta có hệ phương trình.

\(\left\{ \begin{array}{l} a.\frac{2}{3} + b = - 2\\ b = 1 \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} a = - \frac{9}{2}\\ b = 1 \end{array} \right.\)

Vậy \(a = - \frac{9}{2}, b =1\)

b) Vì đồ thị đi qua M(−1;−2) nên ta có phương trình a.(−1)+b = −2.

Tương tự, dựa vào tọa độ của N(99;−2) ta có 99a+b = −2

Vậy, ta có hệ phương trình.

\(\left\{ \begin{array}{l} - a + b = - 2\\ 99a + b = - 2 \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} a = 0\\ b = - 2 \end{array} \right.\)

Vậy a = 0; b = −2.

c) Vì đồ thị đi qua P(4;2) nên ta có phương trình 4a+b = 2.

Tương tự, dựa vào tọa độ của Q(1;1) ta có a+b = 1

Vậy, ta có hệ phương trình.

\(\left\{ \begin{array}{l} 4a + b = 2\\ a + b = 1 \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} a = \frac{1}{3}\\ b = \frac{2}{3} \end{array} \right.\)

Vậy \(a=\frac{1}{3}, b=\frac{2}{3}\)

Viết phương trình đường thẳng y = ax + b ứng với hình sau

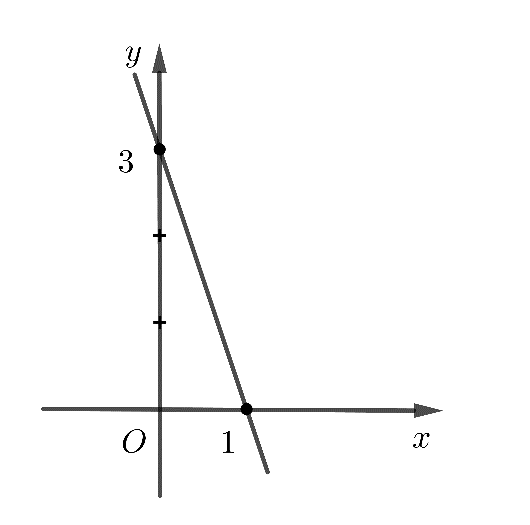
a)

b)

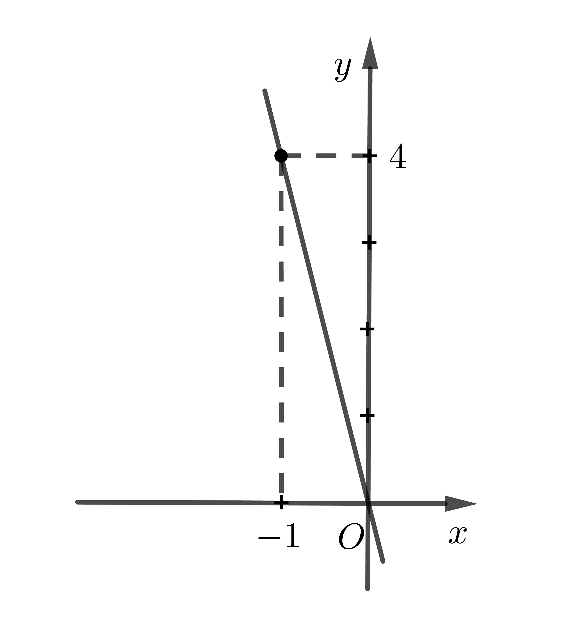
Phương pháp giải

Gọi phương trình tổng quát của đường thẳng sau đó xác định các hệ số a và b ta dựa vào tọa độ các điểm mà đồ thị đi qua, lập hệ phương trình có hai ẩn a và b

Hướng dẫn giải

a) Ta thấy đường thẳng y = ax + b đi qua hai điểm (0;3) và (1;0). Vậy ta có:

\(\left\{ \begin{array}{l}3 = b\\0 = a + b\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = - 3\\b = 3\end{array} \right.\)

Đường thẳng có phương trình là y =  - 3x + 3

b) Ta thấy đường thẳng y = ax + b đi qua hai điểm \(\left( {0;0} \right)\) và \(\left( { - 1;4} \right)\)

Vậy ta có: \(\left\{ \begin{array}{l}0 = b\\4 = a.\left( { - 1} \right) + b\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = - 4\\b = 0\end{array} \right.\)

Đường thẳng có phương trình là y = - 4x

Lập bảng biến thiên và vẽ đồ thị của mỗi hàm số

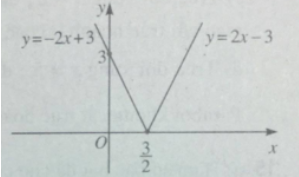
a) y = |2x - 3|

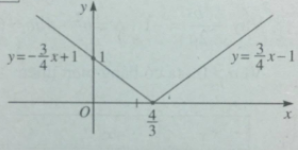
b) y = |-3x / 4 + 1|

c) y = x + |x|

Phương pháp giải

Sử dụng kiến thức về giá trị tuyệt đối 

\(y = |x| = \left\{ \matrix{ x,\text { nếu }x \ge 0 \hfill \cr - x,\text { nếu }x < 0 \hfill \cr} \right.\)

Có tập xác định D = R, đồng biến trên khoảng (0; +∞) và nghịch biến trên khoảng (- ∞; 0)

Đồ thị là đường thẳng; trên nửa khoảng [0; +∞) trùng với đồ thị hàm số y = x và trên khoảng (- ∞; 0) trùng với đồ thị hàm số y = - x

Hướng dẫn giải

a) Ta có thể viết

\(y = \left\{ \begin{array}{l}2x - 3,x \ge \dfrac{3}{2}\\ - 2x + 3,x < \dfrac{3}{2}\end{array} \right.\)

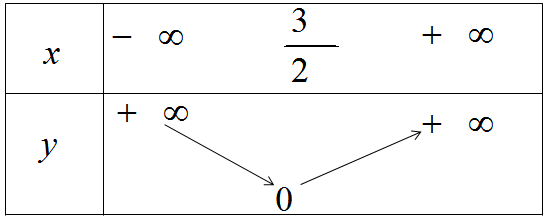
Từ đó có bảng biến thiên và đồ thị của hàm số \(y = |2x - 3|\)(h.32)

b) Ta có thể viết

\(y = \left\{ \begin{array}{l} - \dfrac{3}{4}x + 1,x \le \dfrac{4}{3}\\\dfrac{3}{4}x - 1,x > \dfrac{4}{3}\end{array} \right.\)

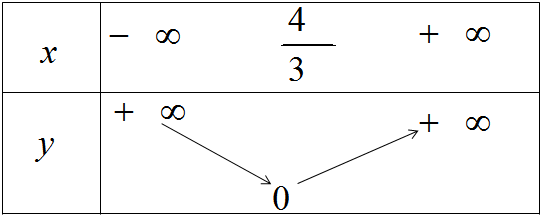
Bảng biến thiên và đồ thị của hàm số \(y = | - \dfrac{3}{4}x + 1|\)(h.33)

c) Với \(x \ge 0\) thì \(y = x + \left| x \right| = x + x = 2x\)

Với x < 0 thì \(y = x + \left| x \right| = x - x = 0\)

Do đó ta có thể viết \(y = \left\{ \begin{array}{l}0,x < 0\\2x,x \ge 0\end{array} \right.\)

Đồ thị của hàm số y = x + |x| được vẽ trên hình 34.

Phương trình đường thẳng song song với đường thẳng y =  - 2x + 21 và đi qua điểm \(P\left( {3;10} \right)\) là

A. y = 2x + 7

B. y =  - 2x + 16

C. y = 3x - 2

D. y =  - 2x + 3

Phương pháp giải

Xét tính đúng sai của từng đáp án bằng cách:

- Kiểm tra hệ số của hai đường thẳng (song song thì a = a').

- Kiểm tra điểm (3; 10) có thuộc đường thẳng hay không và kết luận.

Hướng dẫn giải

Đáp án A, C sai vì hệ số \(a \ne - 2\)

Đáp án B đúng vì hệ số a =  - 2 và \(P\left( {3;10} \right)\) thuộc đường thẳng y =  - 2x + 16

Đáp án D sai vì \(P\left( {3;10} \right)\) không thuộc đường thẳng y =  - 2x + 3

Đáp án đúng B.

Đường thẳng y = ax + b với đồ thị sau có phương trình là

A. \(y = - \dfrac{3}{2}x + 2\)

B. y = 2x - 3

C. \(y = \dfrac{3}{2}x - 3\)

D. y =  - x - 3

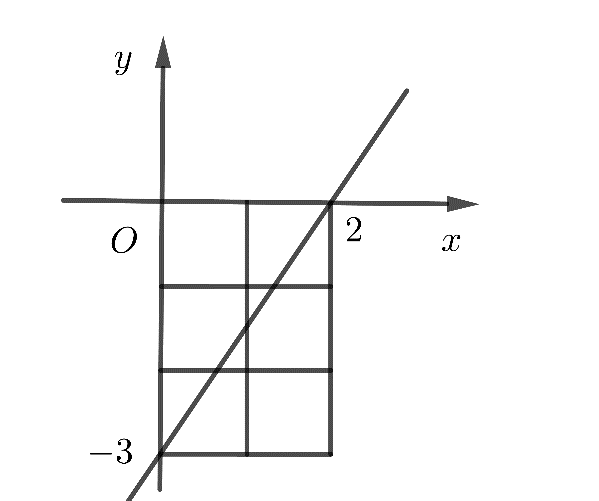
Phương pháp giải

Gọi phương trình tổng quát của đường thẳng sau đó xác định các hệ số a và b ta dựa vào tọa độ các điểm mà đồ thị đi qua, lập hệ phương trình có hai ẩn a và b.

Hướng dẫn giải

Ta thấy đường thẳng y = ax + b đi qua hai điểm \(\left( {2;0} \right)\) và \(\left( {0; - 3} \right)\). Vậy ta có:

\(\left\{ \begin{array}{l}0 = 2a + b\\ - 3 = b\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = - \dfrac{3}{2}\\b = - 3\end{array} \right.\)

Đường thẳng có phương trình là \(y = - \dfrac{3}{2}x - 3\)

Đáp án đúng C

Điểm nào sau đây thuộc đồ thị hàm số \(y = \left| {x + 2} \right| + \left| {3x - 1} \right| + \left| { - x + 4} \right|\) ?

A. \(M\left( {0;7} \right)\)

B. \(N\left( {0;5} \right)\)

C. \(P\left( { - 2; - 1} \right)\)

D. \(Q\left( { - 2;1} \right)\)

Phương pháp giải

Để xét xem một điểm với tọa độ cho trước có thuộc đồ thị của hàm số y = f(x) hay không ta chỉ cần tính giá trị của hàm số tại hoành độ của điểm đã cho. Nếu giá trị của hàm số tại đó bằng tung độ của điểm đang xét thì điểm đó thuộc đồ thị, còn nếu ngược lại thì điểm đang xét không thuộc đồ thị.

Hướng dẫn giải

Thay trực tiếp tọa độ của các điểm vào hàm số ta thấy điểm \(M\left( {0;7} \right)\) thuộc đồ thị của hàm số \(y = \left| {x + 2} \right| + \left| {3x - 1} \right| + \left| { - x + 4} \right|\) vì:

Với x = 0 thì

\(y = \left| {0 + 2} \right| + \left| {3.0 - 1} \right| + \left| { - 0 + 4} \right| \) \(= \left| 2 \right| + \left| { - 1} \right| + \left| 4 \right| = 2 + 1 + 4 = 7\)

Đáp án đúng A