Toán 10 Chương 1 Bài 3: Các phép toán tập hợp

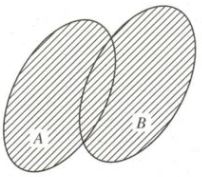
Giao của hai tập hợp A và B, kí hiệu \(A \cap B\) là tập hợp gồm các phần tử vừa thuộc A, vừa thuộc B.

\(A \cap B = \left\{ {x|x \in A\,\,\rm{và}\,\,x \in B} \right\}\)

Hợp của hai tập hợp A và B, kí hiệu \(A \cup B\) là tập hợp các phần tử thuộc A hoặc thuộc B.

\(A \cup B = \left\{ {x|x \in A\,\,\rm{hoặc}\,\,x \in B} \right\}.\)

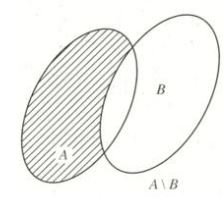
Hiệu của tập hợp A với tập hợp B, kí hiệu A\B là tập gồm các phần tử thuộc A và không thuộc B.

\(A\backslash B = \left\{ {x|x \in A\,\,va\,\,x \notin B} \right\}.\)

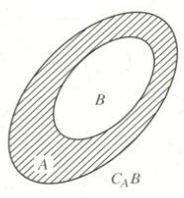
Nếu \(B \subset A\) thì A\B được gọi là phần bù của B trong A, kí hiệu \({C_A}B.\)

Câu 1: Cho \(A = \left\{ {-3; -2; -1; 0; 1; 2; 3} \right\};\,B = \left\{ {x \in \mathbb{N}| x \le 4} \right\}\)

a) Dùng phương pháp liệt kê phần tử xác định các tập hợp B.

b) Xác định các tập hợp sau: \(A \cap B; A \cup B\)

Hướng dẫn giải

a) \(B = \left\{ { 0; 1; 2; 3; 4} \right\}\)

b) \(A \cap B = \left\{ {0; 1;2; 3} \right\}\)

\(A \cup B = \left\{ { - 3; - 2; - 1;0;1;2;3;4} \right\}.\)

Câu 2: Cho \(M = \left\{ {1; 3; 5; 7; 9} \right\}\), \(N = {\rm{\{ }}0;1;2;3;4;5;6\}\), \(P = \left\{ {4;5;6;7;8;9;10} \right\}.\)

Hãy liệt kê các phần tử của các tập hợp dưới đây?

a) \(M \cap (N \cap P);\)

b) \(M \cup (N \cup P);\)

Hướng dẫn giải

a) Ta có: \(N \cap P = \left\{ {4;5;6} \right\}\)

\( \Rightarrow A \cap \left( {B \cap C} \right) = \left\{ {5} \right\}.\)

b) \(N \cup P = \left\{ {0;1;2;3;4;5;6;7;8;9;10} \right\}\)

\( \Rightarrow A \cup \left( {B \cup C} \right) = \left\{ {0;1;2;3;4;5;6;7;8;9;10} \right\}.\)

Câu 1: Cho \(A = \left\{ { - 6; - 5; - 4; - 3; - 2; - 1} \right\},\) \( \,\,B = \left\{ {x \in Z| - 3 \le x \le 2} \right\}\), \(C = \left\{ {x \in R|{x^2} + 2x = 0} \right\}\)

a) Dùng phương pháp liệt kê phần tử xác định các tập hợp B và C.

b) Xác định các tập hợp sau:\(A \cap B,B \cap C,A \cap C.\)

c) Xác định các tập hợp sau:\(A \cup B,B \cup C,A \cup C.\)

d) Xác định các tập hợp sau: \(A\backslash B,B\backslash C,A\backslash C.\)

Câu 2: Cho \(A = \left\{ {1;3;5;7;9;11;13;15} \right\}\), \(B = \{ 9;8;7;6;5;4;3\}\), \(C = \left\{ {1;2;4;5;7;8;10} \right\}.\) Hãy liệt kê các phần tử của các tập hợp dưới đây?

a) \(A \cap (B \cap C);\)

b) \(A \cup (B \cup C);\)

c) \(A \cap \left( {B \cup C} \right);\)

d) \(A \cup (B \cap C).\)

e) \(\left( {A \cap B} \right) \cup C.\)

Câu 1: Một lớp có 45 học sinh. Mỗi em đều đăng ký chơi ít nhất một trong hai môn: bóng đá và bóng chuyền. Có 35 em đăng ký môn bóng đá, 15 em đăng ký môn bóng chuyền. Hỏi có bao nhiêu em đăng ký chơi cả 2 môn?

A. 5

B. 10

C. 25

D. 30

Câu 2: Lớp 10A có 45 học sinh, trong đó có 15 học sinh được xếp loại học lực giỏi, 20 học sinh được xếp loại hạnh kiểm tốt, 10 em vừa xếp loại học lực giỏi, vừa có hạnh kiểm tốt. Hỏi có bao nhiêu học sinh xếp loại học lực giỏi hoặc có hạnh kiểm tốt?

A. 10

B. 25

C. 35

D. 45

Câu 3: Cho A={1;2;3;5;7} và B={2;4;5;6;8}. Tập \(A \cap B\) là

A. \(\left\{ {1;2;3;4;5;6;7;8} \right\}\)

B. \(\left\{ {2;5} \right\}\)

C. \(\left\{ {2} \right\}\)

D. \(\left\{ {5} \right\}\)

Câu 4: Cho hai tập hợp:

\(A = \left\{ {2;4;6;9} \right\}\)

\(B = \left\{ {1;2;3;4} \right\}\)

Tập hợp A\B bằng tập hợp nào sau đây?

A. \(\left\{ {1;2;3;5} \right\}\)

B. \(\left\{ {6;9;1;3} \right\}\)

C. \(\left\{ {6;9} \right\}\)

D. \(\emptyset \)

Câu 5: Cho tập hợp \(A \ne \emptyset .\) Trong các mệnh đề sau, tìm mệnh đề đúng?

A. \(A\backslash \emptyset  = \emptyset \)

B. \(\emptyset \backslash A = A\)

C. \(\emptyset \backslash \emptyset  = A\)

D. \(A\backslash A = \emptyset \)

Qua bài học này, các em cần nắm được những nội dung sau:

• Biết các kí hiện giao, hợp, hiệu, phần bù của hai tập hợp.
• Biết các tìm giao của hai tập hợp, hợp của hai tập hợp, hiệu của hai tập hợp, phân bù của hai tập hợp.