Toán 10 Chương 1 Bài 2: Tập hợp

• Tập hợp là khái niệm cơ bản của toán học, không định nghĩa .

• Tập hợp thường được kí hiệu bằng các chữ cái in hoa như: A, B, C, D, .... các phần tử của tập hợp đặt trong cặp dấu { }.

• Để chỉ phần tử a thuộc tập hợp A ta viết \(a \in A,\) ngược lại ta viết \(a \notin A.\)

• Tập hợp không chứa phần tử nào gọi là tập rỗng. Khí hiệu \(\emptyset .\)

Có 2 cách:

- Cách 1: Liệt kê các phần tử: mỗi phần tử liệt kê một lần, giữa các phần tử có dấu phẩy hoặc dấu chấm phẩy ngăn cách. Nếu số lượng phần tử nhiều có thể dùng dấu ba chấm.

Ví dụ:

A = {2; 4; 6; 8}

B = {0 ; 1; 2; . . . . ; 100 }

C= {0; 2; 4; 6; 8; ...; 20}

- Cách 2: Chỉ rõ tính chất đặc trưng của các phần tử trong tập hợp, tính chất này được viết sau dấu gạch đứng.

Ví dụ:

A = {\(x \in \mathbb{Z}\) | -3 < x < 3}

• Nếu tập A là con của B, kí hiệu: \(A \subset B\) hoặc \(B \supset A.\) .

• Khi đó \(A \subset B \Leftrightarrow \forall x\left( {x \in A \Rightarrow x \in B} \right)\)

Ví dụ:

A={0; 2; 4; 6; 8}, B={1;2;3;...;10}

Cho \(A \ne \emptyset \) có ít nhất 2 tập con là \(\emptyset \) và A.

- Tính chất:    

• \(A \subset A,\emptyset  \subset A\)  với mọi A.
• Nếu \(A \subset B\) và \(B \subset C\) thì \(A \subset C.\)

\(A = B \Leftrightarrow A \subset B\) và \(B \subset A\) hay \(A = B \Leftrightarrow \forall x\left( {x \in A \Leftrightarrow x \in B} \right)\)

Ví dụ:

\(\begin{array}{l}M = \left\{ {x \in \mathbb{R}|x^2+4x+3=0} \right\}\\N = \left\{ {\frac-3;-1} \right\}\\ \Rightarrow M = N.\end{array}\)

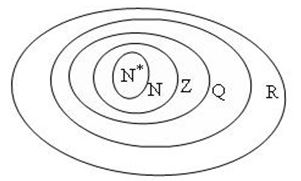
Biểu đồ Ven

Ta có \(\mathbb{N}* \subset \mathbb{N} \subset \mathbb{Z} \subset \mathbb{Q} \subset \mathbb{R}\)

Câu 1: Cho các tập hợp sau:

a) Tập hợp M là các nghiệm của phương trình \((x + 3)(x +5 )\left( {x - \frac{1}{3}} \right) = 0.\)

b) Tập \(N = \left\{ {m \in \mathbb{N}|{m^3} \le 100} \right\}\)

Hãy liệt kê tất cả các phần tử của chúng.

Hướng dẫn giải

a) \(M = \left\{ { - 5; - 3;\frac{1}{3}} \right\}\)

b) \(N = \left\{ { 0; 1; 2; 3; 4} \right\}.\)

Câu 2: Tìm tất cả các tập hợp con của tập hợp \(A = \left\{ { 1; 2; 3} \right\}.\)

Hướng dẫn giải

Tập A có 8 tập hợp con là: \(\emptyset ,\left\{ { 1} \right\},\left\{ 2 \right\},\left\{ 3 \right\},\left\{ { 1; 2} \right\},\left\{ {1; 3} \right\},\left\{ {2; 3} \right\},\left\{ { 1; 2; 3} \right\}.\)

Câu 3: Tìm các tính chất đặc trưng của các tập hợp sau:

a) \(A = \{0; 1; 2; 3;4 ;5; 6;7 ;8 ;9; 10\}\)

b) \(B = \left\{ {\frac{1}{4};\frac{{1}}{9};\frac{{1}}{{16}};\frac{{1}}{{25}};\frac{{1}}{{36}};\frac{{1}}{{49}}} \right\}.\)

Hướng dẫn giải

a) \(A = \{ n \in N, n \le 10 \}.\)

b) \(B = \left\{ {\frac{1}{{{n^2}}}|n \in N,2 \le n \le 7} \right\}\)

Câu 1: Cho các tập hợp sau:

a) Tập hợp A là các nghiệm của phương trình \((x + 3)(x - 5)\left( {2x - 3} \right) = 0.\)

b) Tập \(B = \left\{ {m \in Z| - 10 < {m^3} \le 10} \right\}\)

Hãy liệt kê tất cả các phần tử của chúng.

Câu 2: Tìm tất cả các tập hợp con của tập hợp \(A = \left\{ { - 3; - 2; - 1} \right\}.\)

Câu 3: Tìm các tính chất đặc trưng của các tập hợp sau:

a) \(B = \left\{ {1;\,\,3;\,\,5;\,\,7;\,\,9;\,\,11;\,\,13;\,\,15} \right\}.\)

b) \(A = \left\{ {\frac{1}{2};\frac{1}{5};\frac{1}{{12}};\frac{1}{{20}};\frac{1}{{30}}} \right\}\)

Câu 1: Khẳng định nào sau đây là đúng?

A. \(Q \subset N\)

B. \(N \subset Z\)

C. \(R \subset Q\)

D. \(R \subset Z\)

Câu 2: Tập hợp \(X = \left\{ {0;1;2} \right\}\) có bao nhiêu tập hợp con?

A. 3

B. 6

C. 7

D. 8

Câu 3: Cách viết nào sau đây không đúng?

A. \(1 \subset N\)

B. \(1 \in N\)

C. \(\left\{ 1 \right\} \subset N\)

D. \(1 \in N*\)

Câu 4: Cho tập hợp \(A = \left\{ {1;2;\left\{ {3;4} \right\};x;y} \right\}.\)

Xét các mệnh đề dưới đây:

\(\begin{array}{l}(I):3 \in A\\(II):\left\{ {3;4} \right\} \in A\\(III):\left\{ {a;3;b} \right\} \notin A\end{array}\)

Chọn phương án đúng?

A. Chỉ I đúng.

B. I, II đúng.

C. II, III đúng.

D. Cả I, II, III đều đúng.

Câu 5: Cho các tập hợp:

H= tập hợp các hình bình hành.

V= tập hợp các hình vuông.

N= tập hợp các hình chữ nhật.

T= tập hợp các hình tứ giác.

Trong các mệnh đề sau, tìm mệnh đề sai?

A. \(H \subset T\)

B. \(V \subset N\)

C. \(H \supset V\)

D. \(V \supset N\)

Qua bài học này, các em cần nắm được những nội dung sau:

• Biết được khái niệm tập hợp, tập hợp con, hai tập hợp bằng nhau.
• Xác được được các phần tử của một tập hợp.
• Làm được những bài toán liên quan.