Toán 9 Chương 4 Hình nón - Hình nón cụt - Diện tích xung quanh và thể tích của hình nón, hình nón cụt
Bài giảng dưới đây đã được eLib biên soạn kiến thức cần nhớ chi tiết và cụ thể, các bài tập có hướng dẫn giải giúp các em dễ dàng học tập và vận dụng vào giải các bài tập liên quan. Sau đây mời các em cùng tham khảo.
Mục lục nội dung

Toán 9 Chương 4 Hình nón - Hình nón cụt - Diện tích xung quanh và thể tích của hình nón, hình nón cụt
1. Tóm tắt lý thuyết
1.1. Hình nón
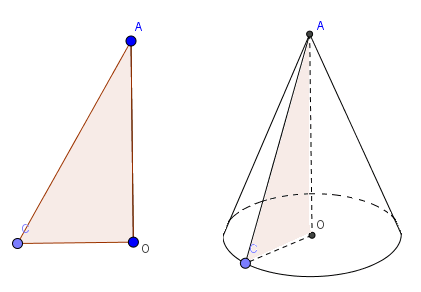
Khi quay một tam giác vuông góc AOC một vòng quanh cạnh góc vuông OA cố định thì được một hình nón.
- Cạnh OC tạo nên đáy của hình nón, là một hình nón tâm O.
- Cạnh AC quét lên mặt xung quanh của hình nón, mỗi vị trí của nó được gọi là một đường sinh, chẳng hạn AD là một đường sinh .
- A là đỉnh và AO là đường cao của hình nón.
1.2. Diện tích - thể tích hình nón
- Diện tích xung quanh của hình nón: Sxq=πrl
- Diện tích toàn phần của hình nón: Stp=πrl+πr2
(r là bán kính đường tròn đáy, l là đường sinh)
- Thể tích hình nón là: V=13πr2h
1.3. Hình nón cụt
Khi cắt hình nón bởi một mặt phẳng song song với mặt đáy, ta được một hình nón cụt.
1.4. Diện tích xung quanh và thể tích hình nón cụt
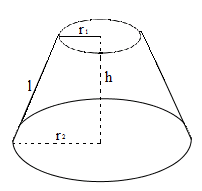
Cho hình nón cụt có r1,r2 là các bán kính đáy, l là độ dài đường sinh, h là chiều cao.
+ Diện tích xung quanh nón cụt là Sxq=π(r1+r2).l
+ Thể tích nón cụt là V=13πh(r21+r22+r1r2)
2. Bài tập minh hoạ
2.1. Bài tập cơ bản
Câu 1: Chiếc nón có dạng mặt xung quanh là một hình nón. Cho biết, đâu là đường tròn đáy, đâu là mặt xung quanh, đâu là đường sinh của nón.
Hướng dẫn giải
Đường tròn đáy là phần vành rộng nhất của nón
Mặt xung quanh là phần bên ngoài của nón, tính từ đỉnh nón đến đường tròn đáy
Đường sinh là đường thẳng bất kì, nối từ đỉnh đến đường tròn đáy
Câu 2: Hình mô tả chiếc nón của một chú hề được tạo bởi hình chóp và 2 hình tròn đồng tâm. Biêt rằng hình tròn nhỏ bỏ trống để chú hề có thể đội được nón.
Cho AB=10cm;OB=6cm,OC=9cm. Tính diện tích để làm chiếc nón ấy
Hướng dẫn giải
Ta thấy chiếc nón chính là diện tích toàn phần của hình nón và phần diện tích hình tròn lớn trừ diện tích hình tròn nhỏ.
Lần lượt tính các giá trị đó, ta có:
Sxq=πrl=π.6.10=60π(cm2)
S(O;OC)=πR2=π.92=81π(cm2)
S(O;OB)=πr2=π.62=36π(cm2)
Diện tích phần còn lại (phần đáy đã chừa đường tròn nhỏ): 81π−36π=45π(cm2)
Vậy diện tích để làm chiếc nón là: 45π+60π=105π(cm2)
2.2. Bài tập nâng cao
Câu 1: Cho hình là hình được ghép bởi một hình nón và một hình trụ, để hai hình này có thể tích bằng nhau thì chiều cao của hình nón phải bằng bao nhiêu lần chiều cao của hình trụ?
Hướng dẫn giải
Do thể tích của hình nón là: V=13πr2h
Thể tích hình trụ là V=πr2h nên tỷ lệ của chúng sẽ là 3
Câu 2: Một hình nón được một mặt phẳng cắt ngang song song với đáy tại trung điểm của đường cao, hình nón được chia ra thành một hình nón cụt và một hình nón. Tỷ lệ thể tích của hình nón mới và hình nón cụt vừa tạo ra là bao nhiêu?
Hướng dẫn giải
Ta sẽ quay lại công thức tính thể tích của mỗi hình để suy ra tỷ lệ:
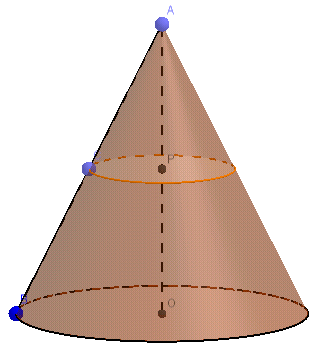
Ở hình bên, ta có P là trung điểm của AO, C là trung điểm của AC.
Dễ dàng suy ra được trong hình chóp cụt, đáy lớn có bán kính gấp đôi đáy bé.
Vchop=13πr2h(dvtt)
Vchopcut=13πh(r2+4r2+2r2)=73πhr2(dvtt)
Vậy, tỷ lệ đề bài yêu cầu đó là 17
3. Luyện tập
3.1. Bài tập tự luận
Câu 1: Cho tam giác ABC vuông tại A, ˆB=60∘ và BC=2a (đơn vị độ dài). Quay tam giác đó một vòng quanh cạnh huyền BC. Hãy tính diện tích xung quanh và thể tích của hình tạo thành.
Câu 2: Cho hình bình hành ABCD với AB=1,AD=x(x>0) và ^BAD=60∘.
a) Tính diện tích toàn phần S của hình tạo thành khi quay hình bình hành ABCD đúng một vòng quanh cạnh AB và diện tích toàn phần S1 của hình tạo thành khi quay quanh cạnh AD.
b) Xác định giá trị x khi S=S1 và S=2S1.
Câu 3: Từ một hình nón, người thợ tiện có thể tiện ra một hình trụ cao nhưng “ hẹp” hoặc một hình trụ rộng nhưng “ thấp”. Trong trường hợp nào thì người thợ tiện loại bỏ ít vật liệu hơn?
Câu 4: Cho tam giác ABC vuông tại A. Gọi V1,V2,V3 theo thứ tự là thể tích của những hình sinh ra khi quay tam giác ABC một vòng xung quanh các cạnh BC,AB và AC. Chứng minh rằng:
1V21=1V22+1V23.
3.2. Bài tập trắc nghiệm
Câu 1: Một hình nón có bán kính đáy là 5cm, đường sinh bằng 13cm. Thể tích hình nón đã cho là:
A. 50π(cm3)
B. 100π(cm3)
C. 200π(cm3)
D. 150π(cm3)
Câu 2: Diện tích xung quanh của hình nón cụt có bán kính đáy lớn đáy nhỏ lần lượt là 15cm,8cm và có đường sinh bằng 10cm là:
A. 70π(cm2)
B. 230π(cm2)
C. 12π(cm2)
D. 1200π(cm2)
Câu 3: Nếu chiều cao và bán kính đáy của một hình nón đều tăng lên và bằng 54 so với các kích thước tương ứng ban đầu thì trong các tỉ số sau đây, tỉ số nào là tỉ số giữa thể tích của hình nón mới với thể tích của hình nón ban đầu?
(A) 54; (B) 1512;
(C) 2516; (D) 12564.
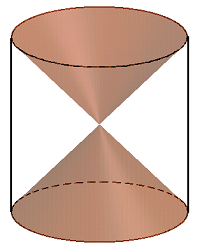
Câu 4: Hình bên mô phỏng 1 chiếc đồng hồ cát, gồm một hình trụ lớn và 2 hình nón đối xứng với nhau.Tỉ số thể tích của tổng hai hình nón và cả hình trụ là:
A. 13
B. 3
C. 23
D. 32
4. Kết luận
Qua bài học này, các em nắm được một số nội dung chính như sau:
- Biết được khái niệm về hình nón: đáy, mặt xung qunh, đường sinh, đường cao, mặt cắt song song với đáy của hình nón và có khái niệm về hình nón cụt.
- Xây dựng được công thức tính diện tích xung quanh và thể tích của hình nón
Tham khảo thêm
- doc Toán 9 Chương 4 Bài 1: Hình trụ - Diện tích xung quanh và thể tích hình trụ
- doc Toán 9 Chương 4 Bài 3: Hình cầu Diện tích hình cầu và thể tích hình cầu
- doc Toán 9 Ôn tập chương 4: Hình trụ - Hình nón - Hình cầu




