Toán 9 Chương 4 Bài 3: Hình cầu Diện tích hình cầu và thể tích hình cầu

Khi quay nửa hình tròn tâm \(O\), bán kính \(R\) một vòng quanh đường kính \(AB\) cố định thì được một hình cầu.

- Điểm \(O\) được gọi là tâm, độ dài \(R\) là bán kính của hình cầu.

- Nửa đường tròn trong phép quay nói trên tạo nên mặt cầu 

Nhắc lại kiến thức đã học ở lớp dưới, ta có công thức sau:

\(S=4\pi R^2=\pi d^2\) (với R là bán kính, d là đường kính của mặt cầu)

Công thức tính thể tích mặt cầu:

\(V=\frac{4}{3}\pi R^3\)

Câu 1: Tính diện tích của một mặt cầu có bán kính bằng \(4cm\)

Hướng dẫn giải

Theo công thức, ta có diện tích của mặt cầu là: \(S=4R^2 \pi=4.4^2\pi=64\pi(cm^2)\)

Câu 2: Khi bán kính của một mặt cầu tăng lên \(\frac{3}{2}\) lần thì diện tích và thể tích của nó thay đổi như thế nào?

Hướng dẫn giải

Theo công thức tính diện tích, ta có \(S=4R^2 \pi\)

Dựa vào công thức trên, khi R tăng lên \(\frac{3}{2}\) thì diện tích tăng lên \(R^2\) lần tức là \(\frac{9}{4}\) lần.

Tương tự đối với thể tích: \(V= \frac{4}{3}\pi R^3\)

khi R tăng lên \(\frac{3}{2}\) thì thể tích tăng lên \(R^3\) lần tức là \(\frac{27}{8}\) lần.

Câu 3: Giả sử trái cam có hình tương tự mặt cầu, bạn Lan cắt trái cam làm đôi và tiến hành đo đường kính của nửa cam vừa cắt, bạn đo được bán kính tính cả vỏ cam là \(2,5cm\), biết vỏ cam dày \(3mm\). Hãy tính thể tích thực của cam mà Lan đã ăn.

Hướng dẫn giải

Xem như phần cam mà Lan đã ăn cũng là một dạng mặt cầu, vậy bán kính của mặt cầu ấy chính là bán kính Lan đo được trừ đi vỏ

Tức là: \(R=25-3=22mm\)

Vậy, thể tích cam mà bạn Lan đã ăn là: \(V= \frac{4}{3}\pi R^3=\frac{4}{3}\pi. 22^3=\frac{42592\pi}{3}(mm^3)\)

Câu 1: Tính bán kính của một mặt cầu, biết rằng mặt cầu đó có số đo đại số diện tích bằng số đo đại số thể tích.

Hướng dẫn giải

Theo đề bài, ta có:

\(\frac{4}{3}\pi R^3=4R^2.\pi\Leftrightarrow \frac{R}{3}=1\Leftrightarrow R=3(dvdd)\)

Câu 2: Tính thể tích của một mặt cầu có bán kính (cm) thỏa mãn phương trình: \(x^2-3x-4=0\) 

Hướng dẫn giải

Giải phương trình trên, ta có được hai nghiệm trái dấu, chỉ chọn nghiệm \(x=4(cm)\)

Vậy, thể tích của mặt cầu đó là \(V=\frac{4}{3}\pi R^3=\frac{4}{3}.4^3.\pi=\frac{256\pi}{3}(cm^3)\)

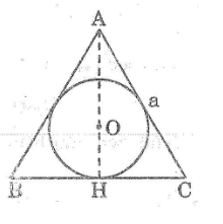
Câu 1: Tam giác đều ABC có độ dài cạnh a,ngoại tiếp một đường tròn.Cho hình quay một vòng xung quanh đường cao AH của tam giác đó (xem hình vẽ), ta được một hình nón ngoại tiếp một hình cầu

Tính thể tích phần hình nón bên ngoài hình cầu

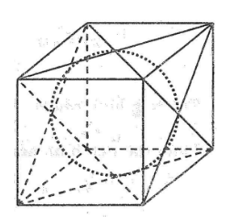
Câu 2: Một quả bóng hình cầu bên trong một hình lập phương như hình bên:

a. Tính tỉ số giữa diện tích toàn phần của hình lập phương với diện tích mặt cầu

b. Nếu diện tích mặt cầu là 7π (cm2) thì diện tích toàn phần của hình lập phương là bao nhiêu ?

c. Nếu bán kính hình cầu là 4cm thì thể tích phần trống (trong hình hộp ngoài hình cầu) là bao nhiêu?

Câu 3: Chọn dưa hấu : với hai quả dưa hấu (xem như là hai hình cầu ) một to và một nhỏ, tỉ số các đường kính của chúng là 5:4 nhưng giá của quả to gấp rưỡi giá của quả nhỏ. Bạn chọn mua quả nào thì lợi hơn (xem chất lượng của chúng như nhau)?

Câu 4: Với một cái thước dây liệu có thể xác định được thể tích của một vật thể có dạng hình cầu hay không?

Câu 1: Trong các hình sau đây, hình nào có diện tích lớn nhất?

(A) Hình tròn có bán kính \(2cm\).

(B) Hình vuông có độ dài cạnh \(3,5cm\).

(C) Tam giác với độ dài các cạnh là \(3cm, 4cm, 5cm\).

(D) Nửa mặt cầu bán kính \(4cm\).

Câu 2: Hai hình cầu \(A\) và \(B\) có các bán kính tương ứng là \(x\) và \(2x\; (cm)\).

Tỉ số các thể tích của \(2\) hình cầu này là:

(A) \(1: 2\)                   (B) \(1: 4\)                  (C) \(1: 8\)                 (D) Một kết quả khác.

Câu 3: Đổ đầy nước vào một dụng cụ để đong có dạng hình nón sau đó đổ hết lượng nước đó vào một hình trụ có bán kính đáy bằng bán kính đáy của hình nón và chiều cao bằng chiều cao của hình nón.Việc làm này lặp lại cho đến khi hình trụ đổ đầy nước thì số lần múc đầy vào hình nón là:

A.1                 B.2                             C.3                             D.4

Câu 4: Chọn câu sai

A. Mặt phẳng cắt qua tâm mặt cầu là đường tròn có diện tích lớn nhất

B. Mặt phẳng cắt qua tâm mặt cầu là đường tròn có chu vi lớn nhất

C. Tại 2 điểm ngoài mặt cầu, ta luôn cắt được đường tròn có diện tích lớn nhất

D. Tại 3 điểm ngoài mặt cầu, ta luôn cắt được đường tròn có diện tích lớn nhất

Câu 5: Thể tích của một mặt cầu là \(\frac{500\pi}{3} (cm^3)\), bán kính của mặt cầu đó là:

A. \(R=5cm\)

B. \(R=6cm\)

C. \(R=7cm\)

D. \(R=8cm\)

Qua bài học này, các em nắm được một số nội dung chính như sau:

• Củng cố các khái niệm của hình cầu, công thức tính diện tích mặt cầu.
• Hiểu cách hình thành công thức tính thể tích hình cầu và biết áp dụng các công thức vào bài tập.