Toán 10 Chương 2 Bài 2: Hàm số y = ax + b

- Hàm số bậc nhất là hàm số được cho bằng biểu thức có dạng $y = {\rm{ax + b}}$ với a, b là những hằng số và ${\rm{a}} \ne {\rm{0}}$.

- Hàm số bậc nhất có tập xác định là R.

• Khi ${\rm{a > 0}}$ hàm số bậc nhất $y = {\rm{ax + b}}$ đồng biến trên R.
• Khi ${\rm{a < 0}}$ hàm số bậc nhất $y = {\rm{ax + b}}$ nghịch biến trên R.

- Đồ thị hàm số $y = {\rm{ax + b}}$ (${\rm{a}} \ne {\rm{0}}$) là một đường thẳng gọi là đường thẳng $y = {\rm{ax + b}}$. Nó có hệ số góc là a và có các đặc điểm sau:

• Không song song và không trùng với các trục tọa độ

• Cắt trục tung tại điểm B(0;b) và cắt trục hoành tại điểm $A(\frac{{ - b}}{a};0)$

- Cho hai đường thẳng $y = a{\rm{x}} + b$ và hàm số $y= a'x + b'$

• Khi a=a' và $b \ne b'$ thì d và d' song song với nhau.

• Khi a=a' và b=b' thì d và d' trùng nhsu.

• Khi $a \ne a'$ thì d và d' cắt nhau.

a) Hàm số bậc nhất trên từng khoảng

• Hàm số bậc nhất trên từng khoảng là sự " lắp ghép" của nhiều hàm số bậc nhất khác nhau.

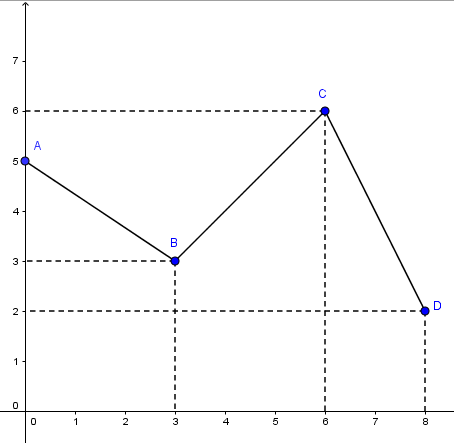
Ví dụ: Vẽ đồ thị của hàm số  $y = \left\{ \begin{array}{l} \frac{{ - 2}}{3}x + 5\,\,\,\,khi\,\,0 \le x \le 0\\ x\,\,\,\,khi\,\,3 \le x \le 6\\ - 2x + 18\,\,\,\,khi\,\,6 \le x \le 8 \end{array} \right.$

Hướng dẫn giải

Để vẽ đồ thị hàm số này, ta vẽ đồ thị của từng hàm số tạo thành chẳng hạn:

AB là phần đồ thị của $y = \frac{{ - 2}}{3}x + 5$ ứng với ${0 \le x \le 3}$ .

BC là phần đồ thị của $y = x$ ứng với ${3 \le x \le 6}$ .

CD là phần đồ thị của $y = - 2x + 18$ ứng với ${6 \le x \le 8}$ .  

Ghép các phần trên lại ta được đồ thị của hàm số đã cho như hình vẽ:

b) Hàm số dạng $y = \left| {ax + b} \right|$

Hàm số dạng $y = \left| {ax + b} \right|$ thực chất cũng là một dạng hàm số bậc thất trên từng khoảng.

Chẳng hạn như khi xét hàm số $y = \left| {3x - 9} \right|$ thì theo định nghĩa trị tuyệt đối thì ta có:

• Nếu $3x - 9 \ge 0$ tức là $x \ge 3$ ,thì $\left| {3x - 9} \right| = 3x - 9$ 

• Nếu $3x - 9 < 0$ tức là $x < 3$ ,thì $\left| {3x - 9} \right| = 9 - 3x$

Do đó hàm số $y = \left| {3x - 9} \right|$ có thể viết là $y = \left\{ {\begin{array}{*{20}{c}} {3x - 9\,\,\,\,\,\,khi\,\,\,x \ge 3}\\ {9 - 3x\,\,\,\,\,\,khi\,\,\,x < 3} \end{array}} \right.$ 

Chú ý: Một cách khá đơn giản để vẽ đồ thị của hàm số $y = \left| {ax + b} \right|$ là ta có thể vẽ  các đường thẳng ax+b và -ax-b rồi xóa đi phần nằm dưới trục hoành. 

Câu 1: Tính a và b để đồ thị hàm số y=ax+b đi qua 2 điểm M(0;4) và N(4;2).

Hướng dẫn giải

Thay tọa độ điểm M(0;4) vào hàm số y=ax+b ta được:

4 = a.0 + b ⇒ b = 4

Thay tọa độ điểm N(4;2) vào hàm số y=ax+b với b=2 ta được:

2 = a.4 + 4 ⇒ a = -1/2

Vậy ta được a=-1/2 và b=2

Câu 2: Tính a và b để đồ thị hàm số y=ax+b đi qua điểm A(4;-2) và song song với đường thẳng y=-x+7.

Hướng dẫn giải

Vì đồ thị hàm số y=ax+b song song với đường thẳng y=x+7 ⇒ a=1

Thay tọa độ điểm A(4;-2) vào hàm số y=ax+b với a=1 ta được:

-2 = 4.1+b ⇒ b=-6

Vậy ta được a=1 và b=-6.

Câu 1: Tính a và b để đồ thị hàm số y=ax+b đi qua 2 điểm A(-1; 3) và B(2; 5).

Câu 2: Tính a và b để đồ thị hàm số y=ax+b đi qua điểm M(3;-2) và song song với đường thẳng y=3x-4

Câu 1: Không vẽ đồ thị, hãy cho biết cặp đường thẳng nào sau đây cắt nhau?

A. $y = {\textstyle{1 \over {\sqrt 2 }}}x - 1;\,y = \sqrt 2 x + 3$

B. $y = {\textstyle{1 \over {\sqrt 2 }}}x;\,y = \frac{{\sqrt 2 }}{2}x - 1$

C. $y = - {\textstyle{1 \over {\sqrt 2 }}}x + 1;\,y = - \left( {\frac{{\sqrt 2 }}{2}x - 1} \right)$

Câu 2: Cho hai đường thẳng ${d_1}:y = \frac{1}{2}x + 100;\,{d_2}:y = - \frac{1}{2}x + 100$. Mệnh đề nào sau đây đúng?

A. Trùng nhau

B. cắt nhau và không vuông góc

C. song song với nhau.

D. vuông góc

Câu 3: Phương trình đường thẳng đi qua hai điểm A(-1 ;2) và B(3 ;1) là:

A. $y = \frac{x}{4} + \frac{1}{4}$

B. $y = \frac{{ - x}}{4} + \frac{7}{4}$

C. $y = \frac{{3x}}{2} + \frac{7}{2}$

D. $y = - \frac{{3x}}{2} + \frac{1}{2}$

Câu 4: Cho hàm số y = x - |x|. Trên đồ thị của hàm số lấy hai điểm A và B hoành độ lần lượt là -2 và 1. Phương trình đường thẳng AB là:

A. $y = \frac{{3x}}{4} - \frac{3}{4}$

B. $y = \frac{{4x}}{3} - \frac{4}{3}$

C. $y = \frac{{ - 3x}}{4} + \frac{3}{4}$

D. $y = - \frac{{4x}}{3} + \frac{4}{3}$

Câu 5: Đồ thị hàm số y = ax + b cắt trục hoành tại điểm x = 3 và đi qua điểm M(-2;4) với các giá trị a, b là:

A. a = 0,5; b = 3

B. a = -0,5 ; b = 3

C. a = -0,5 ; b = -3

D. a = 0,5 ; b = -3

Qua bài học Hàm số y = ax +b, các em cần nắm được các nội dung sau:

• Hàm số bậc nhất
• Khái niệm hàm số y = ax +b và cách vẽ hàm số này.
• Hàm số y = |ax + b|.