Toán 9 Chương 1 Bài 1: Một số hệ thức về cạnh và đường cao trong tam giác vuông
Bài học Một số hệ thức về cạnh và đường cao trong tam giác vuông bao gồm kiến thức thức cần nhớ và các dạng Toán liên quan được eLib tóm tắt một cách chi tiết, dễ hiểu. Sau đây mời các em cùng tham khảo.
Mục lục nội dung

Toán 9 Chương 1 Bài 1: Một số hệ thức về cạnh và đường cao trong tam giác vuông
1. Tóm tắt lý thuyết
1.1. Hệ thức giữa cạnh góc vuông và hình chiếu của nó trên cạnh huyền
Định lý 1: Trong một tam giác vuông, bình phương mỗi cạnh góc vuông bằng tích của cạnh huyền và hình chiếu của cạnh góc vuông đó trên cạnh huyền.
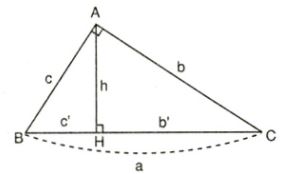
Hình 1
Cụ thể ở hình 1 ta có: Tam giác ABC vuông tại A suy ra:
b2=a.b′ , c2=a.c′
1.2. Một số hệ thức liên quan tới đường cao
Định lý 2: Trong một tam giác vuông, bình phương đường cao ứng với cạnh huyền bằng tích hai hình chiếu của hai cạnh góc vuông trên cạnh huyền.
Cụ thể ở hình 1 ta có: Tam giác ABC vuông tại A suy ra:
h2=b′.c′
Định lý 3: Trong một tam giác vuông, tích hai cạnh góc vuông bằng tích của cạnh huyền và đường cao tương ứng.
Cụ thể ở hình 1 ta có: Tam giác ABC vuông tại A suy ra:
b.c=a.h
Định lý 4: Trong một tam giác vuông, nghịch đảo của bình phương đường cao ứng với cạnh huyền bằng tổng các nghịch đảo của bình phương hai cạnh góc vuông.
Cụ thể ở hình 1 ta có: Tam giác ABC vuông tại A suy ra:
1h2=1b2+1c2 hay h=b.c√b2+c2
Chú ý: Trong các ví dụ và các bài tập tính toán bằng số của chương này, các số đo độ dài ở mỗi bài nếu không ghi đơn vị ta quy ước là cùng đơn vị đo.
2. Bài tập minh họa
2.1. Dạng 1. Bài toán sử dụng Định lý 1
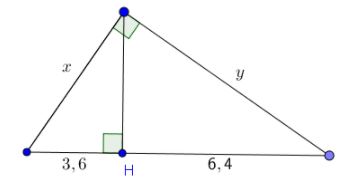
Câu 1: Tính: x,y ở hình dưới đây
Hướng dẫn giải
Áp dụng định lý 1 ta có: x2=3,6.(3,6+6,4)=3,6.10=36⇒x=6
Tương tự: y2=6,4.(3,6+6,4)=6,4.10=64⇒y=8
2.2. Dạng 2. Bài toán sử dụng Định lý 2
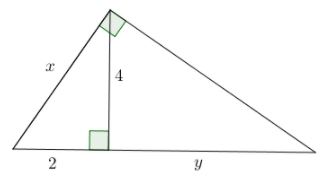
Câu 2: Tính: x,y
Hướng dẫn giải
Áp dụng định lý số 2, ta có: 42=2.y⇒y=8.
Áp dụng định lý 1, ta có: x2=2.(2+8)=2.10=20⇒x=2√5
2.3. Dạng 3. Bài toán sử dụng Định lý 3
Câu 3: Cho tam giác ABC vuông tại A, đường cao AH. Biết AB:AC = 3:4 và AH=12. Tính chu vi tam giác ABC.
Hướng dẫn giải
Đặt: AB=3k,AC=4k⇒BC=√AB2+AC2=√9k2+16k2=5k
Áp dụng định lý 3, ta có: AB.AC=BC.AH⇔3k.4k=5k.12⇒k=5
⇒AB=15;AC=20;BC=25 và P=60
2.4. Dạng 4. Bài toán sử dụng Định lý 4
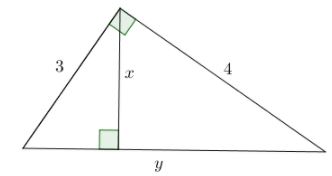
Câu 4: Tính: x,y
Hướng dẫn giải
Áp dụng định lý 4, ta có: 1x2=1b2+1c2⇒x=b.c√b2+c2=3.4√32+42=125
Áp dụng định lý 3, ta có: x.y=3.4⇒y=3.4x=12125=5
(có thể tính y trước bằng định lý pi-ta-go sau đó tính x)
3. Luyện tập
3.1. Bài tập tự luận
Câu 1: Tính x, y trong mỗi hình sau
Câu 2: Cho tam giác ABC vuông tại A, AB : AC = 7 : 24, BC = 625 cm. Tính độ dài hình chiếu của hai cạnh góc vuông trên cạnh huyền.
Câu 3: Cho tam giác ABC vuông tại A, đường cao AH. Biết AC = 20 cm, BH = 9cm. Tính độ dài BC và AH
Câu 4: Cho tam giác ABC vuông tại A, đường cao AH. Biết AB/AC = 20/21 và AH = 420. Tính chu vi tam giác ABC
Câu 5: Cho tam giác ABC vuông tại A, đường cao AH
Cho biết AC/AB = √2; HC - HB = 2cm.Tính:
a) Tỉ số HC : HB
b) Các cạnh của tam giác ABC
3.2. Bài tập trắc nghiệm
Câu 1. Tam giác ABC vuông tại A, đường cao AH. AB = 9cm, AC = 12cm. Tìm khẳng định sai
A. BC =15cm
B. AH=6,2cm
C. BH=5,4cm
D. CH=9,6cm
Câu 2. Cho tam giác OEF vuông tại O có đường cao OI. Có IE =3, IF =12. Tính OE,OF
A. OE=3√5;OF=6√5
B. OE=5√3;OF=3√2
C. OE=4√2;OF=6√3
D. Một đáp số khác
Câu 3. Tam giác ABC vuông tại A, đường cao AI có AB = 13, AI = 12. Diện tích tam giác ABC là:
A. 90,8
B. 189,5
C. 202,8
D. 220
Câu 4. Cho tam giác ABC vuông tại A có đường cao AH=12, Biết BH-CH=7. Độ dài cạnh BC là bao nhiêu
A. BC=23
B. BC=24
C. BC=25
D. BC=26
Câu 5. Tam giác vuông ABC có: AB:AC lần lượt tỉ lệ với 3:4. Biết AH=6. Cạnh BC có độ dài là bao nhiêu
A. BC=11,5
B. BC=12
C. BC=12,5
D. BC=13
4. Kết luận
Qua bài học này, các em cần nắm được những nội dung sau:
- Nắm vững hệ thức giữa cạnh góc vuông và hình chiếu của nó trên cạnh huyền, một số hệ thức liên quan đến đường cao.
- Làm được các bài Toán liên quan.