Lý 12 Bài 1: Dao động điều hòa
Nội dung bài học dưới đây giúp các em nắm được các khái niệm về dao động cơ, dao động tuần hoàn, dao động điều hòa. Viết được phương trình dao động điều hòa và các đại lượng, đặc điểm vectơ vận tốc và gia tốc trong dao động điều hòa. Từ đó giải được các dạng bài tập từ dễ đến khó, nhằm giúp các em ôn tập và củng cố kiến thức. Mời các em cùng tham khảo.
Mục lục nội dung

Lý 12 Bài 1: Dao động điều hòa
1. Tóm tắt lý thuyết
1.1. Khái niệm
- Dao động cơ: là chuyển động qua lại quanh một vị trí cân bằng ( vị trí hợp lực tác dụng lên vật bằng không). VD: chuyển động đung đưa của chiếc lá,...
- Dao động tuần hoàn: là dao động cơ mà sau những khoảng thời gian bằng nhau vật trở lại vị trí cũ theo hướng cũ. Khi vật trở lại vị trí cũ theo hướng cũ thì vật thực hiện được một dao động toàn phần. Thời gian vật thực hiện một dao động toàn phần là một chu kỳ T. Số dao động toàn phần vật thực hiện được trong 1s là tần số f.
1.2. Dao động điều hòa
- Ví dụ dao động điều hòa
Dao động điều hòa.png)
Giả sử M chuyển động theo chiều dương vận tốc góc là ω, P là hình chiếu của M lên Ox.
Tại t = 0, M có tọa độ góc φ
Sau thời gian t, M có tọa độ góc (ωt+ φ)
Khi đó: ¯OP=x;x=OMcos(ωt+φ)¯¯¯¯¯¯¯¯OP=x;x=OMcos(ωt+φ)
Đặt A = OM ta có: x=Acos(ωt+ φ)
Trong đó A, ω, φ là hằng số
Do hàm cosin là hàm điều hòa nên điểm P được gọi là dao động điều hòa.
- Định nghĩa dao động điều hòa
Dao động điều hòa là dao động trong đó li độ của vật là một hàm cosin (hay sin) của thời gian.
- Phương trình dao động điều hòa
Phương trình x=Acos(ωt+ φ) gọi là phương trình của dao động điều hòa.
A là biên độ dao động, là li độ cực đại của vật, A > 0.
ωt+ φ là pha của dao động tại thời điểm t
φ là pha ban đầu tại t = 0 (φ < 0, φ >0, φ = 0)
- Chú ý
- Điểm P dao động điều hòa trên một đoạn thẳng luôn luôn có thể coi là hình chiếu của điểm M chuyển động tròn đều lên đường kính là đoạn thẳng đó.
- Ta quy ước chọn trục x làm gốc để tính pha của dao động và chiều tăng của pha tương ứng với chiều tăng của góc ^MOPˆMOP trong chuyển động tròn đều.
- Chu kì, tần số, tần số góc của dao động điều hòa
Khi vật trở về vị trí cũ hướng cũ thì ta nói vật thực hiện 1 dao động toàn phần.
+ Chu kì (T): của dao động điều hòa là khoảng thời gian để vật thực hiện một dao động toàn phần. Đơn vị là s
+ Tần số (f): của dao động điều hòa là số dao động tuần hoàn thực hiện trong một s. Đơn vị là 1/s hoặc Hz.
+ Tần số góc
Trong dao động điều hòa ω được gọi là tần số góc.
Giữa tần số góc, chu kì và tần số có mối liên hệ: ω=2πT=2πfω=2πT=2πf
- Vận tốc và gia tốc của dao động điều hòa
- Vận tốc
Vận tốc là đạo hàm của li độ theo thời gian.
v=x′=−ωAsin(ωt+φ)
Vận tốc cũng biến thiên theo thời gian.
Tại x= ± A thì v = 0
Tại x = 0 thì v=vmax=ωA
- Gia tốc
Gia tốc là đạo hàm của vận tốc theo thời gian
a=v′=x′′=−ω2Acos(ωt+φ)⇔a=−ω2x
Tại x=0 thì a = 0
Tại x= ± A thì a=amax=ω2A
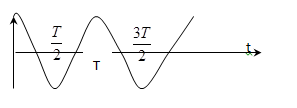
1.3. Đồ thị của dao động điều hòa
Đồ thị trong dao động điều hòa
Đồ thị của dao động điều hòa với φ= 0 có dạng hình sin nên người ta còn gọi là dao động hình sin.
2. Bài tập minh họa
2.1. Dạng 1: Viết phương trình dao động của vật
Một vật dao động điều hòa trên đoạn thẳng dài 4cm với f = 10Hz. Lúc t = 0 vật qua VTCB theo chiều dương của quỹ đạo. Viết phương trình dao động của vật.
Hướng dẫn giải
Ta có tần số góc :
ω=2πf=πA=MN2=2cm
Điều kiện ban đầu t = 0:
x0=0,v0>0⇒φ=−π2⇒x=2cos(20πt−π2)cm
2.2. Dạng 2: Xác định các đại lượng chu kì, biên độ và pha ban đầu
Phương trình của một vật dao động điều hòa có dạng: x=−6cos(πt+π6) (cm). Hãy cho biết chu kì, biên độ và pha ban đầu của dao động.
Hướng dẫn giải
Từ phương trình dao động ta có:
x=−6cos(πt+π6)=−x=6cos(πt+π6−π)(cm)⇒A=6(cm);ω=2π(rad/s);φ=−5π6(rad)
3. Luyện tập
3.1. Bài tập tự luận
Câu 1: Phương trình dao động điều hòa của một vật là: x=6cos(4πt+π6) cm. Xác định li độ, vận tốc và gia tốc của vật khi t = 0,25 s.
Câu 2: Một chất điểm dao động theo phương trình: x = 2,5cos10t cm. Vào thời điểm nào thì pha dao động đạt giá trị π3? Lúc ấy li độ, vận tốc, gia tốc của vật bằng bao nhiêu ?
Câu 3: Một chất điểm dao động điều hòa dọc theo trục Ox có vận tốc bằng không tại hai thời điểm liên tiếp (gần nhau nhất) là t1=1,75s;t2=2,50s; tốc độ trung bình trong khoảng thời gian đó là 16 cm/s. Ở thời điểm t = 0 chất điểm ở cách gốc tọa độ một khoảng là bao nhiêu?
Câu 4: Một vật nhỏ có khối lượng m = 50 g, dao động điều hòa với phương trình: x=20cos(10πt+π2) cm. Xác định độ lớn và chiều của các véctơ vận tốc, gia tốc và lực kéo về tại thời điểm t = 0,75T.
3.2. Bài tập trắc nghiệm
Câu 1: Một vật dao động điều hòa theo phương trình x=Acos(ωt+φ). Tần số góc của dao động là
A. A B. ω
C. φ D. x
Câu 2: Một vật dao động điều hoà với biên độ A = 5cm, khi vật có li độ 2,5cm thì tốc độ của vật là 5√3cm/s. Tốc độ cực đại của dao động là:
A. 10cm/s . B. 8m/s.
C. 8cm/s. D. 10m/s.
Câu 3: Một vật dao động quanh VTCB. Thời điểm ban đầu vật qua VTCB theo chiều dương. Đến thời điểm t1= 13s vật chưa đổi chiều chuyển động và có vận tốc bằng √32 vận tốc ban đầu. Đến thời điểm t2 = 53s vật đã đi được quãng đường 6 cm. Tính vận tốc ban đầu.
A. cm/s B. 2 cm/s
C. 3 cm/s D. 4 cm/s
Câu 4: Một vật dao động điều hòa với phương trình: x=20cos(10πt+π2) cm. Thời điểm đầu tiên vật đi qua vị trí có li độ x = 5 cm theo chiều ngược chiều với chiều dương kể từ thời điểm t = 0.
A. 0,190 s B. 0,194 s
C. 0,192 s D. 0,198 s
3.3. Trắc nghiệm Online
Các em hãy luyện tập bài trắc nghiệm Dao động điều hòa Vật lý 12 sau để nắm rõ thêm kiến thức bài học.
4. Kết luận
Qua bài Dao động điều hòa này, các em cần hoàn thành 1 số mục tiêu mà bài đưa ra như :
- Phát biểu được định nghĩa dao động điều hòa.
- Viết được phương trình của dao động điều hòa và giải thích ý nghĩa các đại lượng có trong phương trình đó như: li độ, biên độ dao động, pha ban đầu.
- Nêu được mối liên hệ giữa dao động điều hòa và chuyển động tròn đều.
Tham khảo thêm
- docx Lý 12 Bài 2: Con lắc lò xo
- docx Lý 12 Bài 3: Con lắc đơn
- docx Lý 12 Bài 4: Dao động tắt dần và dao động cưỡng bức
- pdf Lý 12 Bài 5: Tổng hợp hai dao động điều hòa cùng phương, cùng tần số và Phương pháp Fre-nen
- docx Lý 12 Bài 6: Thực hành: Khảo sát thực nghiệm các định luật dao động của con lắc đơn