Bài 6: Phân phối Chi bình phương - Student và Fisher Snedecor

Giả sử Xi (i = 1, 2, . . . , n) là các đại lượng ngẫu nhiên độc lập, cùng có phân phối chuẩn chính tắc. Xét đại lượng ngẫu nhiên:

${\chi ^2} = \sum\limits_{i = 1}^n {X_i^2}$

Đại lượng ngẫu nhiên ${\chi ^2}$ có phân phối ”chi - bình phương” với n bậc tự do.

Phân phối “chi - bình phương” với n bậc tự do được ký hiệu là: ${\chi ^2} (n)$

Phân phối “chi - bình phương “ được Helmert và Pearson xét đến đầu tiên.

Đồ thị của hàm mật độ fn(x):

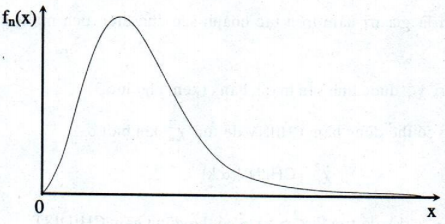
Chú ý: Để tính giá trị của hàm fn(x) và vẽ đồ thị của hàm này, ta có thể dùng các hàm trong Excel (xem phụ lục 1, phần phân phối Chi- bình phương)

Nếu các đại lượng ngẫu nhiên Xi liên hệ với nhau bằng một hệ thức tuyến tính, chẳng hạn $\sum {{X_i}} = n\overline X$ thì số bậc tự do sẽ là n-1

Nếu đại lượng ngẫu nhiên ${\chi ^2}$ phân phối theo qui luật ${\chi ^2}(n)$ [ký hiệu là ${\chi ^2} \sim {\chi ^2} (n)$], thì:

 $E({\chi ^2}) = n;\,\,V{\rm{ar}}({\chi ^2}) = 2n$

Ta ký hiệu $\chi _\alpha ^2$ là giá trị của đại lượng ngẫu nhiên ${\chi ^2}$ có phân phối “chi - bình phương” với n bậc tự do, thỏa mãn điều kiện:

$P({\chi ^2} > \chi _\alpha ^2) = \alpha$

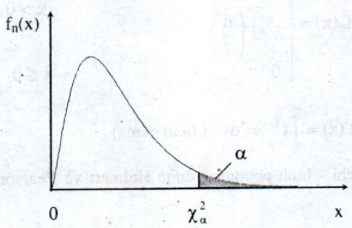
$\chi _\alpha ^2$ chính là giá trị nằm trên tục hoành sao cho diện tích miền gạch chéo bằng a.

Các giá trị $\chi _\alpha ^2$ được tính sẩn thành bảng (xem phụ lục 3)

Ta cũng có thể dùng hàm CHIINV đê tìm  $\chi _\alpha ^2$ khi biết $\alpha$

$\chi _\alpha ^2 = CHIINV(\alpha ,k)$

Cho ${\chi ^2} \sim {\chi ^2}(k)$, đế tìm $P({\chi ^2} > x)$ ta có thể dùng hàm CHIDIST

$P({\chi ^2} > x) = CHIDIST(x,k)$

Khi số bậc tự do tăng lên, phân phối “chi - binh phương “ sẽ xấp xỉ với phân phối chuẩn.

Nếu Z là đại lượng ngẫu nhiên phân phối theo quy luật chuẩn tắc và V là đại lượng ngẫu nhiên độc lập Z, phân phối theo quy luật "chi-bình phương" với n bậc tự do.

Khi đó đại lượng ngẫu nhiên: $T = \frac{Z}{{\sqrt {V/n} }}$ có phân phối Student với n bậc tự do.

Hàm mật độ xác suất của đại lượng ngẫu nhiên T có phân phối Student với n bậc tự do có dạng:

${f_n}(t) = \frac{{\Gamma \left( {\frac{{n + 1}}{2}} \right){{\left( {1 + \frac{{{t^2}}}{n}} \right)}^{ - \frac{{n + 1}}{2}}}}}{{\Gamma \left( {\frac{n}{2}} \right)\sqrt {n\pi } }}$

Phân phối Student với n bậc tự do được ký hiệu là: T(n)

Đồ thị của hàm fn(t):

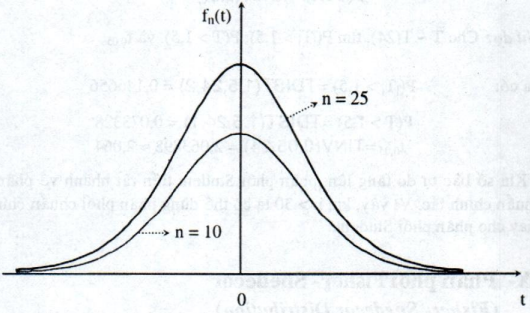
Phân phối Student được W.S Gosset sử dụng lần đầu tiên trong một bài toán thống kê quan trọng và khi viết tác giả lấy bút danh là “Student”.

Nếu đại lượng ngẫu nhiên T có phân phối Student với n bậc tự do [ký hiệu làT~T(n)] thì:

E(T) = 0 và $V{\rm{ar}}(T) = \frac{n}{{n - 2}}$

Để tính giá trị hàm mật độ của đại lượng ngẫu nhiên T ~ T(n) ta có thể sử dụng các hàm trong Excel (xem phụ lục 1, phần phân phối Student)

Ta ký hiệu ${t_\alpha }$ là giá trị của đại lượng ngẫu nhiên T ~ T(n) thỏa mãn điều kiện: ${t_\alpha }>0 \, và \,P(T>{t_\alpha })=\alpha$

Các giá trị ${t_\alpha }$ được tính sẵn thành bảng (xem phụ lục 6)

Ta cũng có thể dùng hàm TINV để tìm ${t_\alpha }$

${t_\alpha }=TINV(\alpha,k)$

Nếu T ~ T(k), để tìm P(|T| > t) (với t > 0) ta có thể dùng hàm TDIST

P(|T| > t) =TDIST(t,k,2)

Nếu T ~ T(k), để tìm P(T > t) với t > 0, ta có thể dùng hàm TDIST

P(T > t) =TDIST(t,k,1 )

Thí dụ: Cho T ~ T(24), tìm P(|T| > 1,5); P(T > 1,5) và t0,05

Ta có:

P(|T| > 1,5) =TDIST(1.5,24,2) = 0,146656

P(T > 1,5) =TDIST(1.5,24,1 ) = 0,073328

t0,05 =TINV(0.05,24) = 2,063898 $\approx$ 2,064

Khi số bậc tự do tăng lên, phân phối Student tiến rất nhanh về phân phối chuẩn chính tắc. Vì vậy, khi n > 30 ta có thể dùng phân phối chuẩn chính tắc thay cho phân phối Student.

Đại lượng ngẫu nhiên F được gọi là có phân phối Fisher - Snedecor với n1 và n2 bậc tự do nếu hàm mật độ xác suất có dạng:

${f_{{n_1},{n_2}}}(x) = \left\{ \begin{array}{l} 0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x \le 0\\ C\frac{{{x^{\frac{{({n_1} - 2)}}{2}}}}}{{{{({n_2} + {n_1}x)}^{\frac{{({n_1} + {n_2})}}{2}}}}}\,\,\,\,\,\,\,\,\,\,\,x > 0 \end{array} \right.$

Trong đó:

$C = \frac{{\Gamma \left( {\frac{{{n_1} + {n_2}}}{2}} \right){n_1}^{\frac{{{n_1}}}{2}}{n_2}^{\frac{{{n_2}}}{2}}}}{{\Gamma \left( {\frac{{{n_1}}}{2}} \right)\Gamma \left( {\frac{{{n_2}}}{2}} \right)}}$

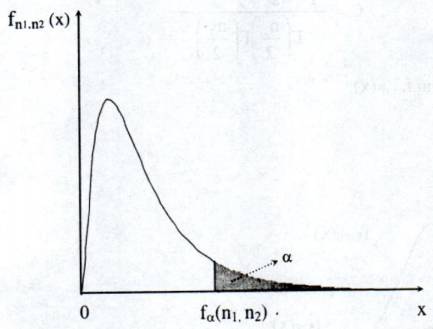
Đồ thị của hàm số ${f_{{n_1},{n_2}}}(x)$

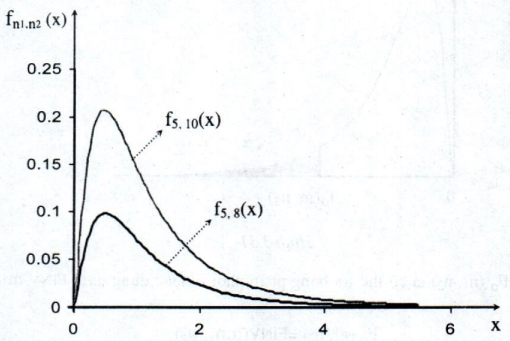
Nếu đại lượng ngẫu nhiên F có phân phối Fisher - Snedecor với bậc tự do n1 và n2 [ký hiệu là F - F(n1, n2)] thì:

$E(F) = \frac{n}{{{n_2} - 2}};\,\,V{\rm{ar}}(F) = \frac{{2n_2^2({n_1} + {n_2} - 2)}}{{{n_1}{{({n_2} - 2)}^2}({n_2} - 4)}}$

Để tính giá trị hàm mật độ của đại lượng ngẫu nhiên F ~ F(n1, n2) ta có thể sử dụng các hàm trong Excel (xem phụ lục 1, phần phân phối Fisher - Snedecor)

Ta ký hiệu $F_\alpha$ (n1, n2) là giá trị của đại lượng ngẫu nhiên F phân phối Fisher - Snedecor với bậc tự do n1, n2 thoả mãn điều kiện:

$P\left[ {F > {F_\alpha }({n_1},{n_2})} \right] = \alpha$

Nếu minh họa $F_\alpha$ trên đồ thị thì $F_\alpha$ là giá trị nằm trên trục hoành sao cho diện tích miền gạch chéo bằng $\alpha$.

Để tìm $F_\alpha$ (n1, n2) ta có thê tra bảng phân phối F hoặc dùng hàm FINV trong Excel

$F_\alpha (n_1,n_2)=FINV(\alpha,n_1,n_2)$

Nếu F ~ F (n1, n2), ta cần tính P(F > x) thì dùng hàm FDIST

P(F > x) =FDIST(x,n1,n2)

Thí dụ: Cho F - F (2, 14), ta cần tính P(F > 1,6) và tìm F0,05

Ta có:

P(F > 1,6) =FDIST(1.6,2, 14) = 0,236699

F0.05 =FINV(0.05,2,14) = 3,73889.

Trên đây là nội dung bài giảng Bài 6: Phân phối Chi bình phương - Student và Fisher Snedecor mà eLib.VN muốn chia sẻ đến các bạn sinh viên. Hy vọng đây sẽ là tư liệu hữu ích giúp các bạn nắm được nội dung bài học tốt hơn. Chúc các bạn học tốt.