Bài 2: Phán đoán đơn

1. Cấu trúc lôgic hình thức của phán đoán đơn

Thí dụ ta có một phán đoán đơn:

"Bản chất con người là tổng hòa các mối quan hệ xã hội".

• Ngôn ngữ học phân tích ngữ pháp của câu đơn (tức là cú pháp), làm rõ đâu là chủ ngữ đâu là vị ngữ và các thành phần khác như bổ ngữ định ngữ, trạng ngữ, v.v..
• Trong trường hợp câu đơn nêu trên "Bản chất con người" là chủ ngữ trong đó danh từ "con người" đóng vai trò tính ngữ bổ nghĩa cho danh từ "bản chất". Động từ "là" đóng vai trò vị ngữ, còn "tổng hòa các mối quan hệ xã hội" đóng vai trò bổ ngữ.
• Logic, học quan tâm trước, hết hai thành tố cơ bản của phán đoán, đó là: Chủ từ logic, ký hiệu là s (viết tắt của chữ La tinh Subjectum); Vị từ logic, ký hiệu là p (viêt tắt của chữ Latinh Praedicatum).

Vận dụng vào trường hợp phán đoán đơn nêu trên, ta có: "Bản chất con người" đóng vai trò chủ từ logic, "tổng hòa các mối quan hệ xã hội" đóng vai trò vị từ logic. Khi đó cấu trúc logic hình thức của phán đoán đơn có dạng:

"S là P"

Nếu ký hiệu "là" bằng dấu gạch nối biểu thị hệ từ logic, thì cấu trúc logic hình thức của phán đoán đơn có dạng:

"S - P"

Đây là dạng thức phổ quát của phán đoán đơn không lệ thuộc vào cấu trúc câu (hay mệnh để ngôn ngữ) cụ thể.

• Xét theo năng lực phản ánh của tư duy, thì chủ từ logic chính là khái niệm đối tượng của phán đoán, vị từ logic là khái niệm vể đặc trưng (dấu hiệu), tức là thuộc tính hoặc là quan hệ, của đối tường đó.
• Phán đoán có nghĩa là liên kết khái niệm về đặc trưng (dấu hiệu) của đối tượng với khái niệm về đối tượng, sự liên kết thực hiện bằng hai thao tác hoặc là khẳng định, hoặc là phủ định, được gọi chung là "hệ từ logic". Hệ từ logic thực chất là một hàm chân lý, nó có thể nhận các giá trị chân thực (đúng đắn) hoặc là giả dối (sai lầm).

Vì cấu trúc lôgic của phán đoán khác biệt với cấu trúc ngữ pháp của câu, cho nên đã có nhiều tìm tòi đặt tên các thành tô logic khác biệt với các thành tố ngữ pháp. Chẳng hạn như trong Nhân minh học Phật giáo, người ta đặt tên như sau:

• Tiền trần - hậu trần
• Tự tính - sai biệt
• Sở biệt - năng biệt
• Hữu pháp - pháp.

Thành tố đứng trước tương ứng Subjectum (S), còn thành tố đứng sau tương ứng Praedicatum (P).

Gần đây có tác giả tìm ra khái niệm khá thích hợp, đó là sở đề (subjectum) và sở thuyết (praedicatum). Theo đó, phán đoán quan niệm như một năng lực giản đơn của lập luận, có cấu trúc logic chung là "Đề - Thuyết", ký hiệu là "Đ - T".

2. Phân loại phán đoán đơn

Phân loai theo chất (của hệ từ lôgic)

• Phán đoán khẳng định. Thí dụ: Arixtốt là nhà lôgíc học Hy Lạp cổ đại.
• Phán đoán phủ định. Thí dụ: Thành phố Hồ Chí Minh không phải là Thủ đô của nước Cộng hòa xã hội chủ nghĩa Việt Nam.

Phân loại theo lượng (của ngoại diên chủ từ lôgic)

• Phán đoán chung (phán đoán toàn thể, phán đoán toàn xưng). Thí dụ: Mọi kim loại đều dẫn điện.
• Phán đoán riêng (phán đoán bộ phận, phán đoán đặc xưng). Thí dụ: Một số sinh viên không học lôgic học.
• Phán đoán đơn nhất (phán đoán đơn xưng). Thí dụ: Hà Nội là Thủ đô của nước Cộng hoà xã hội chủ nghĩa Việt Nam,

Phân loại theo chất và lượng

• Phán đoán khẳng định toàn thể. Thí dụ: Mọi người sinh ra đều bình đẳng.
• Phán đoán khẳng định bộ phận. Thí dụ: Một số sinh viên là vận động viên điền kinh.
• Phán đoán phủ định toàn thể. Thí dụ: Tất cả chúng ta đều không là sinh viên.
• Phán đoán phủ định bộ phận. Thí dụ: Một số người không thích xem bóng đá,

Phân loại theo nói hàm của vị từ lôgic

• Phán đoán thuộc tính (đặc tính). Thí dụ: Bạn tôi là người tốt.
• Phán đoán quan hệ. Thí dụ: Số 5 lớn hơn số 3.
• Phán đoán tồn tại. Thí dụ: Ngày nay vẫn tồn tại những kẻ giết người.

Phân loai theo tình thái

• Phán đoán cái nhiên (khả năng, xác suất). Thí dụ: Ngày mai tròi có thể mưa.
• Phán đoán minh nhiên (hiện thực, hiện hữu). Thí dụ: Bây giờ ở đây đang nắng gắt.
• Phán đoán tất nhiên (tất yếu, tất định). Thí dụ: Sứ không dẫn điện.

Phán đoán đơn đặc tính (hay phán đoán nhất quyết đơn) có thể phân ra thành bốn kiểu loại theo chất và lượng như sau:

• Loại A (viết tắt của chữ Latinh Affirmo), đó là phán đoán khang định chung. Thí dụ: Mọi kim loại đều dẫn điện.
• Loại E (viết tắt của chữ Latinh nEgo), là phán đoán phủ định chung. Thí dụ: Không có á kim nào dẫn điện cả.
• Loại O (viết tát của chữ Latinh negO), là phán đoán phủ định riêng.
• Loại I (viết tắt của chữ Latinh aíELrmo), là phán đoán khẳng định riêng.Thí dụ: Một sô thiên nga không có lông1 màu trắng. Thí dụ: Một số sinh viên là diễn viên.

Hình vuông logic được xâv dựng trên cơ sở A, E; o, I làm thành 4 đỉnh của nó, có dạng như sau:

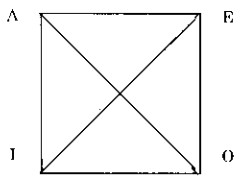
Tương quan giữa bốn loại phán đoán nhất quyết đơn A, E, O, I bao gồm hai loại:

Loại thứ nhất là tương thích, ở đây trước hết là quan hệ thứ bậc, lệ thuộc, cụ thể là I lệ thuộc A và O lộ thuộc E. Xét về mặt giá trị chân lý thì nếu A hoặc E chân thực, tất yếu I hoặc O chân thực; ngược lại, nếu I hoặc O giả dối thì tất yếu A hoặc E giả đối.

Thí dụ 1:

(A) Mọi kim loại dẫn điện - chân thực.

(I) Một số kim loại dẫn điện = chân thực.

Thí dụ 2:

(E) Mọi vật thể không đứng im tuyệt đối - chân thực.

(O) Một số vật thể không đứng im tuyệt đối - chân thực.

Thí dụ 3:

(I) Một số người không ăn uống vẫn sống được = giả dối.

(A) Mọi người không cần ăn uống vẫn sống được = giả dối.

Thí dụ 4:

(O) Một số cá không sông dưới nước = giả đối.

(E) Mọi loài cá đều không sông được dưới nưổc = giả dôi.

Ngoài ra, còn quan hệ: Đối chọi dưới (đối chọi yếu) giữa O và I, không thể cùng giả dối, nhưng có thể cùng chân thực tức là tương thích:

Thí dụ:

Một số thiên nga lông không trắng = chân thực,

Một số thiên nga lông trắng = chân thực

Loại thứ hai là không tương thích, bao gồm:

• Đối chọi trên (đối chọi mạnh) giữa E và A, không thể đồng thời chân thực, nhưng có thể đồng thời giả đối.

Thí dụ:

​(E) Mọi thiên nga lông đều không trắng = giả đối.

(A) Mọi thiên nga lông đều trắng = giả đối.

• Mâu thuẫn (loại trừ nhau) giữa A và 0, E và I, sẽ theo luật bài trung, không thể có trướng hợp cả hai cùng chân thực hoặc cùng giả dối,

Thí dụ 1: (A) Mọi kim loại đều dẫn điện - chân thực. (O) Một sốkim loại không dẫn điện = giả dôi.

Thí dụ 2: (E) Mọi thanh niên đều không hút thuốc lá - giả đối. (I) Một số thanh niên hút thuôc lá = chân thực,

Các loại quan hệ tương thích và không tương thích giữa các phán đoán A, E. Chỉ được biểu thị cụ thể trong hình vuông lôgic như sau:

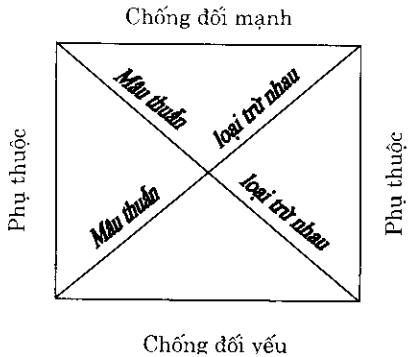
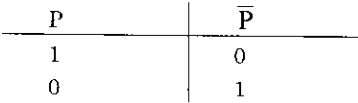
Quan hệ giữa A và O, I và E là quan hệ phủ định nhau. Phán đoán phủ định có giá trị chán lý phụ thuộc vào giá trị khẳng định. Trong lôgic lưỡng trị chỉ có hai giá trị chân lý: chân thật - 1, giả đối = 0. Phép phủ định được định nghĩa bằng bảng giá trị chân lý như sau. Gọi p là ‘phán đoán khẳng định, còn p là phán đoán phủ định, khi đó ta có:

Trong trường hợp này, phủ định của phủ định, ký hiệu là p sẽ có giá trị chân lý trùng khớp với khẳng định ban đầu:

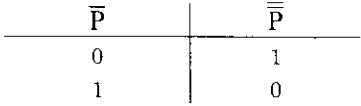
Ta có công thức tương đương lôgic, hay còn gọi là đẳng thức lôgic như sau:  

\(\overline{\overline P} = P\,\,hay\,P = \,\overline{\overline P} \)

Các thuật ngữ S và P trong phán đoán đơn biểu thị các khái niệm. Nếu ngoại diên của khái niệm được bao quát dầv đủ thì người ta gọi thuật ngữ tương ứng là chu diên; trong trường hợp ngược lại, được gọi là không chu diên.

Ta hãy xét tình hình chu diên của các thuật ngữ trong các loại phán đoán A, E, O, I. Ta sẽ sử dụng hai loại ký hiệu biểu trưng.

• Loại thứ nhất: Ký hiệu thuật ngữ chu diên bằng dấu (+) đi kèm sau thuật ngữ đó; trường hợp ngược lại, không chu diên, sẽ ký hiệu bằng dấu (-) đi kèm sau thuật ngữ tương ứng.
• Loại thứ hai, sử dụng sơ đồ Gi. Ven (J.Venn), biểu thị ngoại diên khái niệm, tức là tập hợp đối tượng được khái niệm bao quát bằng đường cong khép kín: nếu chu diên thì biểu thị bằng đường liền nét, ngược lại thì biểu thị bằng đường không liền nét. Cụ thể như sau:

Phán đoán loại A có hai trường hợp:

Trường hợp thứ nhất: (S+; P-)

Quan hệ lệ thuộc 

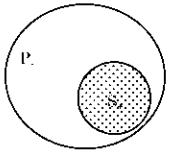
Trường hợp thứ hai: (S +, P+)

Quan hệ tương đương.

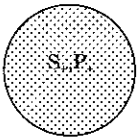
Ngoại lệ, A là phán đoán định nghĩa khái niệm. 

Thí dụ: Hình vuông là hình có 4 cạnh bằng nhau và 4 góc bằng nhau.

Phán đoán loại E có một trường hợp: S+; P+

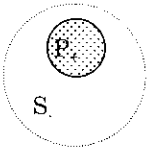
Phán đoán loại O có hai trường hợp:

Trường hợp thứ nhất: S., P+

Trường hợp thứ hai: S., P+

Phán đoán loại l có hai trường hợp:

Trường hợp thứ nhất: S-, P-

Trường hợp thứ hai: S., P+

Trên đây là nội dung bài giảng Logic học Bài 2: Phán đoán đơn mà eLib.VN muốn chia sẻ đến các bạn sinh viên. Hy vọng đây sẽ là tư liệu hữu ích giúp các bạn nắm được nội dung bài học tốt hơn. Chúc các bạn học tốt!