Giải bài tập SGK Toán 9 Bài: Luyện tập
eLib xin chia sẻ với các em học sinh lớp 9 nội dung giải bài tập SGK bài Hình hộp chữ nhật bên dưới đây. Với nội dung đầy đủ 8 bài tập trang 76 đi kèm đó là phương pháp và hướng dẫn giải chi tiết, hi vọng rằng đây sẽ là tài liệu giúp các em học tập tốt hơn. Sau đây mời các em cùng tham khảo.
Mục lục nội dung

Giải bài tập SGK Toán 9 Bài: Luyện tập
1. Giải bài 19 trang 76 SGK Toán 9 tập 2
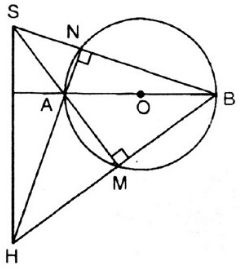
Cho đường tròn tâm O, đường kính AB và S là một điểm nằm bên ngoài đường tròn. SA và SB lần lượt cắt đường tròn tại M, N. Gọi H là giao điểm của BM và AN. Chứng minh rằng SH vuông góc với AB.
Phương pháp giải
Chỉ ra SM⊥HB và HN⊥SB
Xét tam giác SHB, chứng minh được AB⊥SH
Hướng dẫn giải
Ta có:
^AMB=90o (góc nội tiếp chắn nửa đường tròn)
Suy ra SM⊥HB
^ANB=90o (góc nội tiếp chắn nửa đường tròn)
Suy ra HN⊥SB
Xét tam giác SHB có:
SM và HN là hai đường cao cắt nhau tại A.
Nên A là trực tâm của tam giác SHB
Suy ra AB⊥SH
2. Giải bài 20 trang 76 SGK Toán 9 tập 2
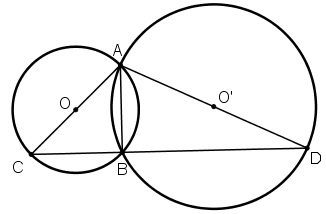
Cho hai đường tròn (O) và (O') cắt nhau tại A và B. Vẽ các đường kính AC và AD của hai đường tròn. Chứng minh rằng ba điểm C, B, D thẳng hàng.
Phương pháp giải
Sử dụng góc nội tiếp chắn nửa đường tròn là góc vuông.
Xét đường tròn (O) chứng minh ^ABC=90o
Xét đường tròn (O') chứng minh ^ABD=90o
Từ đó chứng minh ^ABC+^ABD=180∘
Hướng dẫn giải
Xét đường tròn (O) vì AC là đường kính nên ^ABC là góc nội tiếp chắn nửa đường tròn hay ^ABC=90o
Suy ra AB⊥CB (1)
Xét đường tròn (O') vì AD là đường kính nên ^ABD là góc nội tiếp chắn nửa đường tròn hay ^ABD=90o
Suy ra AB⊥DB (2)
Suy ra ^ABC+^ABD=90∘+90∘=180∘ nên ^CBD=180∘⇒C,B,D thẳng hàng.
3. Giải bài 21 trang 76 SGK Toán 9 tập 2
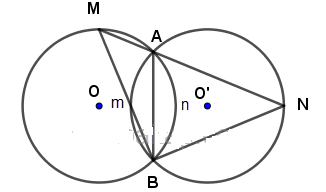
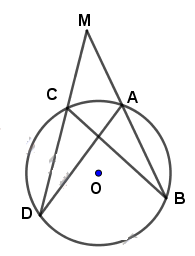
Cho hai đường tròn bằng nhau (O) và (O') cắt nhau tại A và B. Vẽ đường thẳng qua A cắt (O) tại M và cắt (O') tại N (A nằm giữa M và N). Hỏi MBN là tam giác gì? Tại sao?
Phương pháp giải
Ta chỉ cần chứng minh ⌢AmB=⌢AnB
Hướng dẫn giải
Hai đường tròn (O) và (O') bằng nhau cắt nhau tại hai điểm A và B nên ⌢AmB=⌢AnB
Trong đường tròn (O), ta có ^AMB là góc nội tiếp chắn cung ⌢AnB
Trong đường tròn (O'), ta có ^ANB là góc nội tiếp chắn cung ⌢AnB
Suy ra ^AMB=^ANB
Vậy tam giác BMN là tam giác cân tại B
4. Giải bài 22 trang 76 SGK Toán 9 tập 2
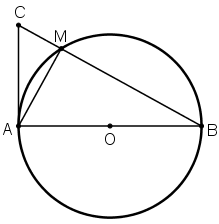
Trên đường tròn (O) đường kính AB, lấy điểm M (khác A và B). Vẽ tiếp tuyến của (O) tại A. Đường thẳng BM cắt tiếp tuyến đó tại C. Chứng minh rằng ta luôn có: MA2=MB.MC
Phương pháp giải
+ Góc nội tiếp chắn nửa đường tròn là góc vuông.
+ Tiếp tuyến của đường tròn (O) tại A là đường thẳng qua A và vuông góc với bán kính OA.
Hướng dẫn giải
Vì AC là tiếp tuyến của đường tròn (O) tại A nên OA⊥AC hay tam giác ABC vuông tại A.
Lại có ^AMB là góc nội tiếp chắn nửa đường tròn nên ^AMB=90o.
Xét tam giác ABC vuông tại A có AM⊥BC có:
MA2=MB.MC (hệ thức lượng trong tam giác vuông)
5. Giải bài 23 trang 76 SGK Toán 9 tập 2
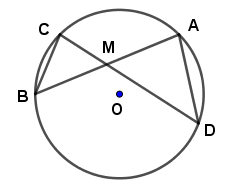
Cho đường tròn (O) và một điểm M cố định không nằm trên đường tròn. Qua M kẻ hai đường thẳng. Đường thẳng thứ nhất cắt (O) tại A và B. Đường thẳng thứ hai cắt (O) tại C và D. Chứng minh MA.MB=MC.MD.
Phương pháp giải
Xét cả hai trường hợp điểm M nằm bên trong và bên ngoài đường tròn. Trong mỗi trường hợp, xét hai tam giác đồng dạng.
TH1: M nằm bên trong đường tròn.
Trong đường tròn (O), ta có:
^ABC=^ADC (hai góc nội tiếp cùng chắn cung AC).
Xét hai tam giác AMD và CMB có:
+) ^ADC=^ABC (cmt)
+) ^AMD=^CMB (đối đỉnh)
Suy ra ΔAMD∽ΔCMB (g.g)
TH2: M nằm bên ngoài đường tròn
Trong đường tròn (O), ^ABC=^ADC ( hai góc nội tiếp cùng chắn cung AC)
Xét hai tam giác AMD và CMB có:
+) ^ADC=^ABC (cmt)
+) ˆM chung.
Suy ra ΔAMD∽ΔCMB (g.g)
Hướng dẫn giải
TH1: M nằm bên trong đường tròn.
Trong đường tròn (O), ta có:
^ABC=^ADC (hai góc nội tiếp cùng chắn cung AC).
Xét hai tam giác AMD và CMB có:
+) ^ADC=^ABC (cmt)
+) ^AMD=^CMB (đối đỉnh)
Suy ra ΔAMD∽ΔCMB (g.g)
Có AMMC=MDMB⇒MA.MB=MD.MC (cặp cạnh tương ứng)
TH2: M nằm bên ngoài đường tròn
Tương tự, ta có:
Trong đường tròn (O), ^ABC=^ADC ( hai góc nội tiếp cùng chắn cung AC)
Xét hai tam giác AMD và CMB có:
+) ^ADC=^ABC (cmt)
+) ˆM chung.
Suy ra ΔAMD∽ΔCMB (g.g)
Có AMMC=MDMB⇒MA.MB=MD.MC (cặp cạnh tương ứng)
6. Giải bài 24 trang 76 SGK Toán 9 tập 2
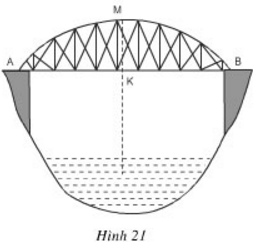
Một chiếc cầu được thiết kế như hình 21 có độ dài AB = 40m, chiều cao MK = 3m. Hãy tính bán kính của đường tròn chứa cung AMB.
Phương pháp giải
(Biểu diễn bài toán như hình vẽ)
- Gọi MN là đường kính đi qua M là điểm chính giữa cung AB.
- Chứng minh ΔKAM∽ΔKNB, từ đó tính R
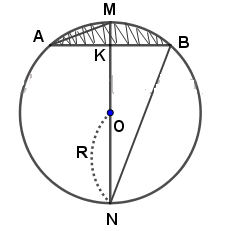
Hướng dẫn giải
Kẻ MN vuông góc với AB tại K.
Khi đó: MN=2R là đường kính của đường tròn chứa cung tròn AMB.
Theo định lý về đường kính và dây cung ta có: K là trung điểm của AB nên KA=KB=20m
Xét hai tam giác KAM và KNB có:
+) ^AKM=^BKN=90o
+) ^MAK=^BNK (hai góc nội tiếp cùng chắn cung MB)
Suy ra ΔKAM∽ΔKNB (g.g)
Có KAKN=KMKB
Thay số:
202R−3=320⇒2R−3=4003⇒R=4096≈68,2m
Vậy bán kính đường tròn chứa cung AMB dài 68,2 m
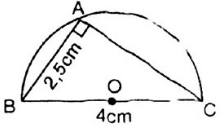
7. Giải bài 25 trang 76 SGK Toán 9 tập 2
Dựng một tam giác vuông, biết cạnh huyền dài 4cm và một cạnh góc vuông dài 2,5cm.
Phương pháp giải
Góc nội tiếp chắn một nửa đường tròn là góc vuông.
Hướng dẫn giải
Cách vẽ như sau:
- Vẽ đoạn thẳng BC dài 4cm.
- Vẽ nửa đường tròn đường kính BC.
- Vẽ đường tròn tâm B bán kính 2,5cm cắt nửa đường tròn đường kính BC tại A.
Ta có tam giác thỏa mãn các yêu cầu của đề bài.
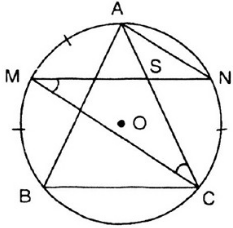
8. Giải bài 26 trang 76 SGK Toán 9 tập 2
Cho AB,BC,CA là ba dây của đường tròn (O). Từ điểm chính giữa M của cung AB vẽ dây MN song song với dây BC. Gọi giao điểm của MN và AC là S. Chứng minh SM=SC và SN=SA.
Phương pháp giải
Ta cần chứng minh tam giác SAN và tam giác SMC cân tại S.
Hướng dẫn giải
* Vì điểm M là điểm chính giữa của cung AB nên ta có: ⌢AM=⌢BM
Lại có MN // BC (theo bài 13 trang 72) suy ra ⌢MB=⌢NC
Do đó: ⌢AM=⌢NC
⇒^ACM=^NMC (hai góc nội tiếp chắn hai cung bằng nhau)
Vậy tam giác SMC cân tại S suy ra SM = SC.
Tương tự ta cũng có: ^ANM=^NAC ( hai góc nội tiếp chắn hai cung bằng nhau)
Suy ra tam giác SAN cân tại S hay SA = SN
Tham khảo thêm
- doc Giải bài tập SGK Toán 9 Bài 1: Góc ở tâm. Số đo cung
- doc Giải bài tập SGK Toán 9 Bài: Luyện tập
- doc Giải bài tập SGK Toán 9 Bài 2: Liên hệ giữa cung và dây
- doc Giải bài tập SGK Toán 9 Bài 3 Góc nội tiếp
- doc Giải bài tập SGK Toán 9 Bài 4: Góc tạo bởi tia tiếp tuyến và dây cung
- doc Giải bài tập SGK Toán 9 Bài: Luyện tập
- doc Giải bài tập SGK Toán 9 Bài 5: Góc có đỉnh ở bên trong đường tròn. Góc có đỉnh ở bên ngoài đường tròn
- doc Giải bài tập SGK Toán 9 Bài: Luyện tập
- doc Giải bài tập SGK Toán 9 Bài 6: Cung chứa góc
- doc Giải bài tập SGK Toán 9 Bài: Luyện tập