Giải bài tập SGK Toán 8 Bài: Luyện tập

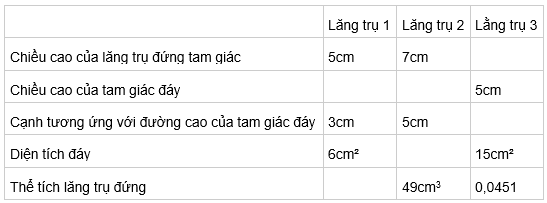
Điền số thích hợp vào các ô trống ở bảng sau:

Phương pháp giải

+) \(S = \dfrac{1}{2}. a.h \Rightarrow  h = \dfrac{2S}{a}\) và  \(a = \dfrac{2S}{h}\);

 +) \( V = S. h_1  \Rightarrow S = \dfrac{V}{h_1}\)  và  \(h_1 = \dfrac {V}{S} \)

Trong đó \(V\) là thể tích của lăng trụ, \(S\) là diện tích đáy, \(h_1\) là chiều cao của lăng trụ đứng tam giác,  \(h\) là chiều cao của tam giác đáy, \(a\) là cạnh tương ứng với đường cao của tam giác đáy. 

Hướng dẫn giải

Với \(V\) là thể tích của lăng trụ, \(S\) là diện tích đáy, \(h_1\) là chiều cao của lăng trụ đứng tam giác,  \(h\) là chiều cao của tam giác đáy, \(a\) là cạnh tương ứng với đường cao của tam giác đáy.

+) Lăng trụ 1 : \(h_1=5cm, a=3cm, S=6cm^2\)

 \(h = \dfrac{2S}{a} = \dfrac{2.6}{3} = 4(cm) \)

 \(V = S.h_1 = 6.5 = 30(cm^3) \) 

+) Lăng trụ 2: \(h_1=7cm, a=5cm, V=49cm^3\)

 \(S = \dfrac{V}{h_{1}}= \dfrac{49}{7}= 7(cm^2) \) 

 \(h =\dfrac{2S}{a} = \dfrac{2.7}{5} = \dfrac{14}{5}(cm) \)

+) Lăng trụ 3: \(h=5cm, S=15cm^2, V=0,045l\) 

Ta có \(0,045l = 0,045dm^3= 45(cm^3) \) 

 \(h_1=\dfrac{V}{S} =  \dfrac{45}{15} = 3(cm) \)

 \(a = \dfrac{2S}{h}  = \dfrac{2.15}{5}= 6 (cm) \) 

Điền vào bảng, ta được kết quả sau: 

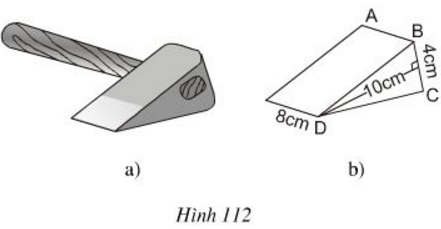
Hình 112b biểu diễn một lưỡi rìu bằng sắt, nó có dạng một lăng trụ đứng, BDC là một tam giác cân.

a) Hãy vẽ thêm nét khuất, điền thêm chữ vào các đỉnh rồi cho biết AB song song với những cạnh nào?

b) Tính thể tích lưỡi rìu.

c) Tính khối lượng của lưỡi rìu, biết khối lương riêng của sắt là 7,874 kg/dm3 (phần cán gỗ bên trong lưỡi rìu là không đáng kể).

Phương pháp giải

- Thể tích \( V=S.h\), trong đó \( S\) là diện tích đáy, \(h \) là chiều cao.

- Khối lượng lưỡi rìu = khối lượng riêng \( \times \) thể tích lưỡi rìu.

Hướng dẫn giải

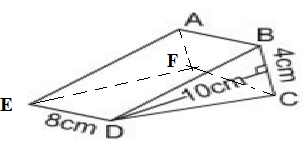
a) Vẽ thêm nét khuất, ta được hình sau. Cạnh AB song song với những cạnh FC, ED.

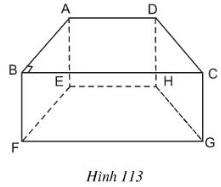
Hình 113 là một lăng trụ đứng, đáy là hình thang vuông.

Hãy kể tên:

a) Các cạnh song song với cạnh AD.

b) Cạnh song song với cạnh AB.

c) Các đường thẳng song song với mặt phẳng (EFGH).

d) Các đường thẳng song song với mặt phẳng (DCGH).

Phương pháp giải

Dựa vào tính chất của hình lăng trụ đứng và giả thiết đề bài cho đáy là hình thang vuông.

Hướng dẫn giải

a) Các cạnh song song với cạnh \(AD\) là: \(EH, BC, FG\).

b) Cạnh song song với \(AB\) là \(EF\).

c) Các đường thẳng song song với mặt phẳng \((EFGH)\) là: \(AD, BC, AB, CD.\)

d) Các đường thẳng song song với mặt phẳng \((DCGH)\): \(AE, BF.\)

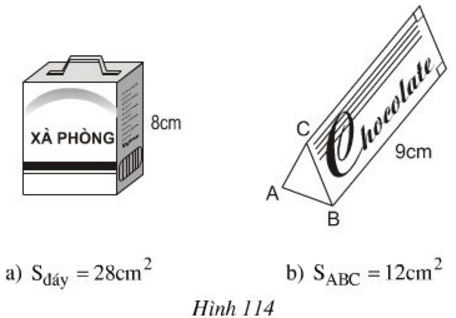
Tính thể tích của hộp xà phòng và hộp sô-cô-la trên hình 114, biết:

a) Diện tích đáy hộp xà phòng là \(28cm^2 \)

b) Diện tích tam giác \(ABC\) ở hình 114b là \(12cm^2 \)

Phương pháp giải

Áp dụng công thức tính thể tích: \( V=S.h\), trong đó \( S\) là diện tích đáy, \(h \) là chiều cao.

Hướng dẫn giải

a) Thể tích hộp xà phòng là:

\( V = S.h = 28.8 = 224 (cm^3 )\)

b) Thể tích của hộp sô – cô – la là :

\(V = S. h = 12.9 = 108 (cm^3) \)

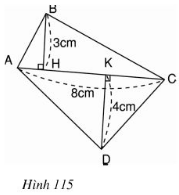
Đáy của một lăng trụ đứng là tứ giác, các kích thước cho theo hình 115. Biết chiều cao của lăng trụ là 10cm. Hãy tính thể tích của nó.

Phương pháp giải

Áp dụng các công thức: 

+) Thể tích:\( V=S.h\), trong đó \( S\) là diện tích đáy, \(h \) là chiều cao.

+) \(S_{ABCD}= S_{ABC}+ S_{ADC}\).

+) Diện tích tam giác: \( S=a.h_1\), trong đó \( a\) là độ dài đáy, \(h_1 \) là chiều cao tương ứng với độ dài đáy của tam giác.

Hướng dẫn giải

Diện tích đáy của lăng trụ là diện tích của tứ giác \(ABCD\).

Ta có:

\(S_{ABCD}= S_{ABC}+ S_{ADC}\).

\(= \dfrac{1}{2} .AC.BH + \dfrac{1}{2}.AC. DK \) 

\(= \dfrac{1}{2} .8.3 + \dfrac{1}{2}. 8.4 = 12 + 16 = 28\,cm^2  \)

Thể tích của lăng trụ là:

\(V = S.h = 28.10 = 280 (cm^3) \)