Giải bài tập SGK Toán 8 Bài 9: Hình chữ nhật
Phần hướng dẫn giải bài tập Hình chữ nhật sẽ giúp các em nắm được phương pháp và rèn luyện kĩ năng, giải bài tập từ SGK Hình học 8 Tập 1
Mục lục nội dung
1. Giải bài 58 trang 99 SGK Toán 8 tập 1
2. Giải bài 59 trang 99 SGK Toán 8 tập 1
3. Giải bài 60 trang 99 SGK Toán 8 tập 1
4. Giải bài 61 trang 99 SGK Toán 8 tập 1
5. Giải bài 62 trang 99 SGK Toán 8 tập 1
6. Giải bài 63 trang 100 SGK Toán 8 tập 1
7. Giải bài 64 trang 100 SGK Toán 8 tập 1

Giải bài tập SGK Toán 8 Bài 9: Hình chữ nhật
1. Giải bài 58 trang 99 SGK Toán 8 tập 1
Điền vào chỗ trống, biết rằng a,b là độ dài các cạnh, d là độ dài đường chéo của một hình chữ nhật
.png)
Phương pháp giải
Áp dụng định lý Pytago.
Hướng dẫn giải
Cột thứ hai
Áp dụng định lí Pytago vào tam giác vuông ABC có ^ABC=90o, ta có:
d2=a2+b2=52+122=25+144=169
Nên d=√169=13
Cột thứ ba
Áp dụng định lí Pytago vào tam giác vuông ABC có ^ABC=90o, ta có:
a2+b2=d2
⇒a2=d2−b2=(√10)2−(√6)2
=10−6=4⇒a=√4=2
Cột thứ tư
Áp dụng định lí Pytago vào tam giác vuông ABC có ^ABC=90o, ta có:
a2+b2=d2
⇒b2=d2−a2=72−(√13)2
=49−13=36⇒b=√36=6
Vậy ta có được bảng sau
.png)
2. Giải bài 59 trang 99 SGK Toán 8 tập 1
Chứng minh rằng
a) Giao điểm hai đường chéo cuẩ hình chữ nhật là tâm đối xứng củahình chữ nhật đó.
b) Hai đường thẳng đi qua trung điểm hai cặp cạnh đối của hình chữ nhật là hai trục đối xứng của hình chữ nhật đó.
Phương pháp giải
Áp dụng
- Định lí: Giao điểm hai đường chéo của hình bình hành là tâm đối xứng của hình bình hành đó.
- Định nghĩa: Điểm O gọi là tâm đối xứng qua hình H nếu điểm đối xứng với mỗi điểm thuộc hình H qua điểm O cũng thuộc hình H.
- Hình thang cân nhận đường thẳng đi qua trung điểm hai đáy làm trục đối xứng.
- Hình chữ nhật cũng là 1 hình thang cân.
Hướng dẫn giải
Câu a
.png)
Giả sử ABCD là hình chữ nhật. Gọi O là giao điểm của AC và BD.
Theo tính chất đường chéo của hình chữ nhật ta có; hai đường chéo bằng nhau và cắt nhau tại trung điểm mỗi đường.
Vậy: OA = OC và OB= OD
Do đó, O là tâm đối xứng của hình chữ nhật đó.
Câu b
.png)
Áp dung tính chất: Đường thẳng đi qua trung điểm hai đáy của hình thang cân là trục đối xứng của hình thang cân đó.
ABCD là hình chữ nhật
⇒ ABCD là hình thang cân (hai đáy AB và CD)
⇒ Đường thẳng đi qua trung điểm AB và CD là trục đối xứng ABCD.
Tương tự vậy: ABCD cũng là hình thang cân với hai đáy AD và BC
⇒ Đường thẳng đi qua trung điểm AD và BC là trục đối xứng của ABCD
Vậy ta có điều phải chứng minh.
3. Giải bài 60 trang 99 SGK Toán 8 tập 1
Tính độ dài đường trung tuyến ứng với cạnh huyền của một tam giác vuông có các cạnh góc vuông bằng 7cm và 24cm
Phương pháp giải
Áp dụng
- Định lí Pytago.
- Tính chất: Trong tam giác vuông, trung tuyến ứng với cạnh huyền có độ dài bằng nửa độ dài cạnh ấy.
Hướng dẫn giải
Gọi a là độ dài cạnh huyền của tam giác vuông.
Theo định lý Pi-ta-go ta có:
a2=72+242=625
⇒a=25cm
Trung tuyến ứng với cạnh huyền có độ dài bằng nửa độ dài cạnh huyền
Vậy độ dài đường trung tuyến ứng với cạnh huyền là 12,5cm
4. Giải bài 61 trang 99 SGK Toán 8 tập 1
Cho tam giác ABC, đường cao AH. Gọi I là trung điểm của AC,E là điểm đối xứng với H qua I. Tứ giác AHCE là hình gì? Vì sao?
Phương pháp giải
Áp dụng dấu hiệu nhận biết hình chữ nhật: Hình bình hành có một góc vuông là hình chữ nhật.
Hướng dẫn giải
.png)
Theo giả thiết I là trung điểm của AC nên IA=IC (tính chất trung điểm)
Vì E là điểm đối xứng với H qua I (giả thiết) nên I là trung điểm của HE hay IE=IH (tính chất đối xứng)
Do đó, tứ giác AHCE có hai đường chéo AC,HE cắt nhau tại trung điểm I của mỗi đường nên AHCE là hình bình hành (dấu hiệu nhận biết hình bình hành)
Mặt khác AH là đường cao trong tam giác ABC nên ^AHC=900
Do đó AHCE là hình chữ nhật (dấu hiệu nhận biết hình chữ nhật)
5. Giải bài 62 trang 99 SGK Toán 8 tập 1
Các câu sau đúng hay sai?
a) Nếu tam giác ABC vuông tại C thì điểm C thuộc đường tròn có đường kính là AB (h.88)
b) Nếu điểm C thuộc đường tròn có đường kính là AB (C khác A và B) thì tam giác ABC vuông tại C (h.89)
.png)
.png)
Phương pháp giải
Áp dụng tính chất: Trong tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng nửa cạnh ấy.
Hướng dẫn giải
Câu a: Đúng.
Gọi O là trung điểm của AB. Ta có CO là trung tuyến ứng với cạnh huyền AB của tam giác vuông ACB
⇒OC=12AB hay OC=OA=OB (Trong tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng nửa cạnh ấy)
Nên A,B,C cùng thuộc đường tròn bán kính OA. Vậy C thuộc đường tròn đường kính AB.
Câu b: Đúng.
Gọi O là tâm đường tròn. Suy ra CO=AO=OB (= bán kính) mà AB là đường kính nên AB=2R
Suy ra CO=AO=OB=AB2
Tam giác ABC có trung tuyến CO và CO bằng nửa cạnh AB (chứng minh trên ) nên tam giác ABC vuông tại C (trong tam giác có đường trung tuyến ứng với một cạnh bằng nửa cạnh ấy thì tam giác đó là tam giác vuông).
6. Giải bài 63 trang 100 SGK Toán 8 tập 1
Tìm x trên hình 90
.png)
Phương pháp giải
Áp dụng
- Dấu hiệu nhận biết hình chữ nhật: Tứ giác có ba góc vuông là hình chữ nhật.
- Định lí Pytago: Bình phương cạnh huyền bằng tổng các bình phương hai cạnh góc vuông.
Hướng dẫn giải
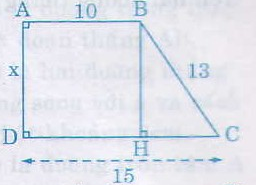
Kẻ BH⊥CD
Tứ giác ABHD có ˆA=ˆD=ˆH=900 (giả thiết)
⇒ Tứ giác ABHD là hình chữ nhật (dấu hiệu nhận biết hình chữ nhật)
⇒ DH=AB=10 (tính chất hình chữ nhật)
Ta có: HC=DC−DH=15−10=5.
Áp dụng định lí Pytago vào tam giác vuông BHC vuông tại H ta có:
BH2=BC2−HC2=132−52=169−25=144BH=x=√144=12
Vậy x=12.
7. Giải bài 64 trang 100 SGK Toán 8 tập 1
Cho hình bình hành ABCD. Các tia phân giác cảu các góc A, B, C, D cắt nhau như trên hình 91. Chứng minh rằng EFGH là hình chữ nhật.
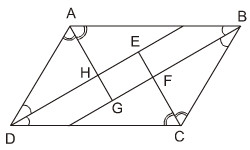
Phương pháp giải
Áp dụng
- Định lí: Tổng 3 góc của một tam giác bằng 180o.
- Dấu hiệu nhận biết hình chữ nhật: Tứ giác có ba góc vuông là hình chữ nhật.
Hướng dẫn giải
Theo giả thiết ABCD là hình bình hành nên AD//BC,AB//CD
Vì AD//BC ⇒^DAB+^ABC=1800 (hai góc trong cùng phía bù nhau)
Vì AG là tia phân giác ^DAB (giả thiết)
⇒ ^BAG=^DAH=12^DAB (tính chất tia phân giác)
Vì BG là tia phân giác ^ABC (giả thiết)
⇒ ^ABG=12^ABC
Do đó: ^BAG+^ABG=12(^DAB+^ABC)=12.1800=900
Xét ΔAGB có:
^BAG+^ABG=900
Áp dụng định lí tổng ba góc trong một tam giác vào tam giác AGB ta có:
^BAG+^ABG+^AGB=1800
⇒^AGB=1800−(^BAG+^ABG)=1800−900=900 (*)
+ Vì AB//DC ⇒^DAB+^ADC=1800 (hai góc trong cùng phía bù nhau)
+ Vì DE là tia phân giác ^ADC (giả thiết)
⇒ ^ADH=^EDC=12^ADC (tính chất tia phân giác)
Do đó: ^DAH+^ADH=12(^DAB+^ADC)=12.1800=900
Áp dụng định lí tổng ba góc trong một tam giác vào tam giác ADH ta có:
^DAH+^ADH+^AHD=1800
⇒^AHD=1800−(^DAH+^ADH)=1800−900=900
Suy ra AH⊥HD nên ^EHG=900 (**)
Chứng minh tương tự:
Ta có: ^DCB+^ADC=1800 (hai góc trong cùng phía bù nhau)
Mà ^ECD=12^DCB (do CE là phân giác góc DCB)
Nên ^EDC+^ECD=12(^ADC+^DCB)=12.1800=900
Lại có
^EDC+^ECD+^DEC=1800 (tổng ba góc trong tam giác DEC)
⇒^DEC=1800−(^EDC+^ECD)=1800−900=900
Hay ^HEF=900 (***)
Từ (*), (**) và (***) ta thấy tứ giác EFGH có ba góc vuông nên là hình chữ nhật (dấu hiệu nhận biết hình chữ nhật)
8. Giải bài 65 trang 100 SGK Toán 8 tập 1
Tứ giác ABCD có hai đường chéo vuông góc với nhau. Gọi E, F, G, H theo thứ tự là trung điểm của các cạnh AB, BC, CD, DA. Tứ giác EFGH là hình gì ? Vì sao ?
Phương pháp giải
Áp dụng
- Đường trung bình của tam giác song song với cạnh thứ ba và bằng nửa cạnh ấy.
- Dấu hiệu nhận biết hình chữ nhật: Hình bình hành có một góc vuông là hình chữ nhật.
Hướng dẫn giải
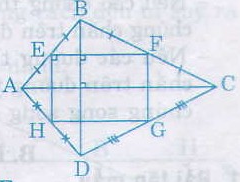
Vì E,F lần lượt là trung điểm của AB,BC (giả thiết)
⇒ EF là đường trung bình của ∆ABC (dấu hiệu nhận biết đường trung bình của tam giác)
⇒ EF//AC và EF=AC2 (1) (tính chất đường trung bình của tam giác)
Do G,H lần lượt là trung điểm của CD,DA (giả thiết)
⇒ HG là đường trung bình của ∆ADC (dấu hiệu nhận biết đường trung bình của tam giác)
⇒ HG//AC và HG=AC2 (2) (tính chất đường trung bình của tam giác)
Từ (1) và (2) ⇒ EF//HG và EF=HG(=AC2)
⇒ EFGH là hình bình hành (dấu hiệu nhận biết hình bình hành)
Vì E,H lần lượt là trung điểm của AB,AD (giả thiết)
⇒ EH là đường trung bình của ∆ABD (dấu hiệu nhận biết đường trung bình của tam giác)
⇒ EH//BD (tính chất đường trung bình của tam giác)
Ta có: EF//AC và EH//BD mà AC⊥BD nên EF⊥EH
Hay ^FEH=900
Hình bình hành EFGH có ˆE=900 nên là hình chữ nhật (theo dấu hiệu nhận biết hình chữ nhật).
9. Giải bài 66 trang 100 SGK Toán 8 tập 1
Đố. Một đội công nhân đang trồng cây trên đoạn đường AB thì gặp chướng ngại vật che lấp tầm nhìn (h.92). Đội đã dựng các điểm C, D, E như trên hình vẽ rồi trồng cây tiếp trên đoạn thẳng EF vuông góc với DE. Vì sao AB và EF cùng nằm trên một đường thẳng ?
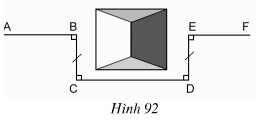
Phương pháp giải
Áp dụng
- Dấu hiệu nhận biết hình chữ nhật: Hình bình hành có một góc vuông là hình chữ nhật.
- Tính chất hình chữ nhật.
- Dấu hiệu nhận biết ba điểm thẳng hàng.
Hướng dẫn giải
Tứ giác BCDE có
BC//DE (vì cùng vuông góc với CD)
BC=DE (giả thiết)
⇒ Tứ giác BCDE là hình bình hành (dấu hiệu nhận biết hình bình hành)
Mà ^BCD=900 (giả thiết)
⇒ Hình bình hành BCDE là hình chữ nhật (dấu hiệu nhận biết hình chữ nhật)
⇒ ^CBE=^BED=900
Mặt khác: ^CBA=^FED=900 (giả thiết)
Ta có: ^CBA+^CBE=900+900=1800
⇒A,B,E thẳng hàng (1)
^FED+^BED=900+900=1800
⇒ B,E,F thẳng hàng (2)
Từ (1) và (2) ⇒ AB và EF cùng nằm trên một đường thẳng
Tham khảo thêm
- doc Giải bài tập SGK Toán 8 Bài 1: Tứ giác
- doc Giải bài tập SGK Toán 8 Bài 2: Hình thang
- doc Giải bài tập SGK Toán 8 Bài 3: Hình thang cân
- doc Giải bài tập SGK Toán 8 Bài 4: Đường trung bình của tam giác, của hình thang
- doc Giải bài tập SGK Toán 8 Bài 5: Dựng hình bằng thước và compa. Dựng hình thang
- doc Giải bài tập SGK Toán 8 Bài 6: Đối xứng trục
- doc Giải bài tập SGK Toán 8 Bài 7: Hình bình hành
- doc Giải bài tập SGK Toán 8 Bài 8: Đối xứng tâm
- doc Giải bài tập SGK Toán 8 Bài 10: Đường thẳng song song với một đường thẳng cho trước
- doc Giải bài tập SGK Toán 8 Bài 11: Hình thoi
- doc Giải bài tập SGK Toán 8 Bài 12: Hình vuông




