Giải bài tập SGK Toán 10 Ôn tập chương 2: Tích vô hướng của hai vectơ và ứng dụng
Hướng dẫn Giải bài tập SGK Hình học 10 Bài Ôn tập chương 2: Tích vô hướng của hai vectơ và ứng dụng sẽ giúp các em học sinh nắm vững phương pháp giải bài tập và ôn luyện tốt kiến thức. Mời các em cùng theo dõi.
Mục lục nội dung
1.1. Giải bài 1 trang 62 SGK Hình học 10
1.2. Giải bài 2 trang 62 SGK Hình học 10
1.3. Giải bài 3 trang 62 SGK Hình học 10
1.4. Giải bài 4 trang 62 SGK Hình học 10
1.5. Giải bài 5 trang 62 SGK Hình học 10
1.6. Giải bài 6 trang 62 SGK Hình học 10
1.7. Giải bài 7 trang 62 SGK Hình học 10
1.8. Giải bài 8 trang 62 SGK Hình học 10
1.9. Giải bài 9 trang 62 SGK Hình học 10
1.10. Giải bài 10 trang 62 SGK Hình học 10
1.11. Giải bài 11 trang 62 SGK Hình học 10
2.1. Giải bài 1 trang 63 SGK Hình học 10
2.2. Giải bài 2 trang 63 SGK Hình học 10
2.3. Giải bài 3 trang 63 SGK Hình học 10
2.4. Giải bài 4 trang 63 SGK Hình học 10
2.5. Giải bài 5 trang 63 SGK Hình học 10
2.6. Giải bài 6 trang 63 SGK Hình học 10
2.7. Giải bài 7 trang 63 SGK Hình học 10
2.8. Giải bài 8 trang 64 SGK Hình học 10
2.9. Giải bài 9 trang 64 SGK Hình học 10
2.10. Giải bài 10 trang 64 SGK Hình học 10
2.11. Giải bài 11 trang 64 SGK Hình học 10
2.12. Giải bài 12 trang 64 SGK Hình học 10
2.13. Giải bài 13 trang 64 SGK Hình học 10
2.14. Giải bài 14 trang 64 SGK Hình học 10
2.15. Giải bài 15 trang 65 SGK Hình học 10
2.16. Giải bài 16 trang 65 SGK Hình học 10
2.17. Giải bài 17 trang 65 SGK Hình học 10
2.18. Giải bài 18 trang 65 SGK Hình học 10
2.19. Giải bài 19 trang 65 SGK Hình học 10
2.20. Giải bài 20 trang 65 SGK Hình học 10
2.21. Giải bài 21 trang 65 SGK Hình học 10
2.22. Giải bài 22 trang 65 SGK Hình học 10
2.23. Giải bài 23 trang 66 SGK Hình học 10
2.24. Giải bài 24 trang 66 SGK Hình học 10
2.25. Giải bài 25 trang 66 SGK Hình học 10
2.26. Giải bài 26 trang 66 SGK Hình học 10
2.27. Giải bài 27 trang 66 SGK Hình học 10
2.28. Giải bài 28 trang 66 SGK Hình học 10

Giải bài tập SGK Toán 10 Ôn tập chương 2: Tích vô hướng của hai vectơ và ứng dụng
1. Câu hỏi và bài tập
1.1. Giải bài 1 trang 62 SGK Hình học 10
Hãy nhắc lại định nghĩa giá trị lượng giác của một góc α với 00≤α≤1800. Tại sao khi α là một góc nhọn thì giá trị lượng giác này lại chính là các tỉ số lượng giác đã được học ở lớp 9?
Phương pháp giải
- Nhắc lại định nghĩa.
- Sử dụng định nghĩa để tính các tỉ số lượng giác của góc nhọn sẽ thấy nó chính là các tỉ số lượng giác đã được học ở lớp 9.
Hướng dẫn giải
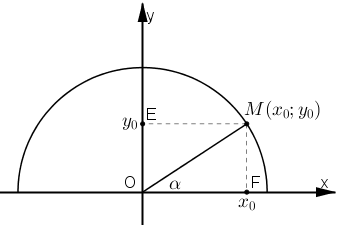
- Định nghĩa: Với mỗi góc α (00≤α≤1800) ta xác định một điểm M trên nửa đường tròn đơn vị sao cho ^xOM=α và giả sử điểm M có tọa độ M(x0;y0).
Khi đó ta có định nghĩa:
sinα=y0
cosα=x0
tanα=y0x0
cotα=x0y0
Các số sinα,cosα,tanα,cotα được gọi là các giá trị lượng giác của góc α.
- Khi α là các góc nhọn thì:
Trong tam giác OFM vuông tại F, ta có:
sinα=MFOM=y01=y0
cosα=OFOM=x01=x0
tanα=FMOF=y0x0
cotα=OFFM=x0y0
1.2. Giải bài 2 trang 62 SGK Hình học 10
Tại sao hai góc bù nhau lại có sin bằng nhau và cosin đối nhau?
Phương pháp giải
Sử dụng đường tròn lượng giác tính sin và cosin của hai góc bù nhau rồi so sánh.
Hướng dẫn giải
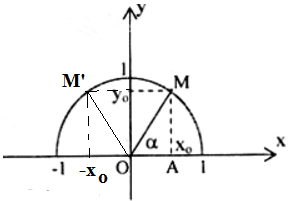
Gọi M(x0;y0) nằm trên nửa đường tròn đơn vị sao cho ^xOM=α.
Khi đó điểm M′(−x0;y0) trên nửa đường tròn đơn vị có ^xOM′=1800−α tức là ^xOM′ là góc bù với ^xOM=α.
Do đó: sinα=y0=sin(180−α), cosα=x0=−(−x0)=−cos(1800−α).
1.3. Giải bài 3 trang 62 SGK Hình học 10
Nhắc lại định nghĩa tích vô hướng của hai vecto →a và →b. Tích vô hướng này với |→a| và |→b| không đổi đạt giá trị lớn nhất và nhỏ nhẩt khi nào?
Phương pháp giải
Sử dụng định nghĩa tích vô hướng của hai véc tơ:
→a.→b=|→a|.|→b|.cos(→a,→b)
Hướng dẫn giải
−1≤cos(→a,→b)≤1⇒−1.|→a|.|→b|≤|→a|.|→b|cos(→a,→b)≤|→a|.|→b|.1⇒−|→a|.|→b|≤→a.→b≤|→a|.|→b|
→a.→b đạt giá trị lớn nhất |→a|.|→b| khi:
cos(→a,→b)=1⇒(→a,→b)=00
tức là →a và →b cùng hướng.
→a.→b đạt giá trị nhỏ nhất −|→a|.|→b| khi:
cos(→a,→b)=−1⇒(→a,→b)=1800 hay →a và →b ngược hướng.
1.4. Giải bài 4 trang 62 SGK Hình học 10
Trong mặt phẳng Oxy cho vectơ →a=(−3;1) và vectơ →b=(2;2). Hãy tính tích vô hướng →a.→b.
Phương pháp giải
Sử dụng công thức tính tích vô hướng:
Với →a=(a1;a2);→b=(b1;b2)⇒→a.→b=a1b1+a2b2
Hướng dẫn giải
Ta có →a=(−3;1) và vecto →b=(2;2) nên:
→a.→b=(−3).2+1.2=−6+2=−4.
1.5. Giải bài 5 trang 62 SGK Hình học 10
Hãy nhắc lại định lí cosin trong tam giác. Từ các hệ thức này hãy tính cosA,cosB,cosC theo các cạnh của tam giác.
Phương pháp giải
- Sử dụng định lý cosin chuyển vé đổi dấu để được cosA,cosB,cosC theo các cạnh của tam giác.
Hướng dẫn giải
Định lí cosin:
Trong tam giác ABC có AB=c, BC=a, AC=b ta có:
a2=b2+c2−2bc.cosA⇒cosA=b2+c2−a22bcb2=c2+a2−2ca.cosB⇒cosB=c2+a2−b22cac2=a2+b2−2ab.cosC⇒cosC=a2+b2−c22ab
1.6. Giải bài 6 trang 62 SGK Hình học 10
Từ hệ thức a2=b2+c2−2bc.cosA trong tam giác, hãy suy ra định lí Py-ta-go.
Phương pháp giải
Áp dụng hệ thức cho tam giác ABC vuông tại A có góc A bằng 90 độ.
Hướng dẫn giải
Ta có: a2=b2+c2−2bc.cosA
Khi góc A=900, suy ra cosA=0
Do đó ta có: a2=b2+c2−2bc.cos900 =b2+c2−2bc.0=b2+c2
Vậy a2=b2+c2 (định lí Py-ta-go).
1.7. Giải bài 7 trang 62 SGK Hình học 10
Chứng minh rằng với mọi tam giác ABC, ta có a=2RsinA;b=2RsinB;c=2RsinC, trong đó R là bán kính đường tròn ngoại tiếp tam giác ABC.
Phương pháp giải
Ta sử dụng định lí sin: asinA=bsinB=csinC=2R
Hướng dẫn giải
Ta có:
asinA=2R⇒a=2RsinAbsinB=2R⇒b=2RsinBcsinC=2R⇒c=2RsinC
Vậy a=2RsinA;b=2RsinB;c=2RsinC
1.8. Giải bài 8 trang 62 SGK Hình học 10
Cho tam giác ABC. Chứng minh rằng:
a) Góc A nhọn khi và chỉ khi a2<b2+c2
b) Góc A tù khi và chỉ khi a2>b2+c2
c) Góc A vuông khi và chỉ khi a2=b2+c2
Phương pháp giải
- Sử dụng hệ quả của đinh lí cosin.
- Góc A nhọn thì ⇔cosA>0.
- Góc A tù thì ⇔cosA<0.
- Góc A vuông thì ⇔cosA=0.
Hướng dẫn giải
Câu a:
Theo hệ quả định lí cosin: cosA=b2+c2−a22bc.
Khi đó:
a2<b2+c2⇔b2+c2−a2>0
Mà 2bc>0 nên b2+c2−a22bc>0
⇔cosA>0
⇔A là góc nhọn.
Vậy góc A nhọn khi và chỉ khi a2<b2+c2
Câu b:
a2>b2+c2⇔b2+c2−a2<0
Mà 2bc>0 nên b2+c2−a22bc<0
⇔cosA<0
⇔A là góc tù.
Vậy góc A tù khi và chỉ khi a2>b2+c2
Câu c:
Theo định lí Py-ta-go thì: a2=b2+c2
⇔ góc A là góc vuông.
Cách trình bày khác:
Góc A vuông ⇔cosA=cos900=0
⇔b2+c2−a22bc=0 ⇔b2+c2−a2=0 ⇔b2+c2=a2
1.9. Giải bài 9 trang 62 SGK Hình học 10
Cho tam giác ABC có góc A=600,BC=6. Tính bán kính đường tròn ngoại tiếp tam giác đó.
Phương pháp giải
Sử dụng định lí sin thay số vài để tìm R.
asinA=bsinB=csinC=2R
Hướng dẫn giải
Sử dụng định lí sin, ta có:
asinA=bsinB=csinC=2R
Mà a=BC=6, ˆA=600 nên
6sin600=2R ⇔R=62sin600 =62.√32=6√3=2√3
1.10. Giải bài 10 trang 62 SGK Hình học 10
Cho tam giác ABC có a=12,b=16,c=20. Tính diện tích S tam giác, chiều cao ha, các bán kính R,r của các đường tròn ngoại tiếp, nội tiếp tam giác và đường trung tuyến ma của tam giác.
Phương pháp giải
- Diện tích tam giác S=√p(p−a)(p−b)(p−c)
- Chiều cao: S=12aha⇒ha=2Sa
- Bán kính đường tròn ngoại tiếp tam giác: S=abc4R⇒R=abc4S
- Bán kính đường tròn nội tiếp tam giác: S=pr⇒r=Sp
- Trung tuyến: m2a=2(b2+c2)−a24
Hướng dẫn giải
- Tính diện tích: Sử dụng công thức Hê-rông với:
p=a+b+c2=12+16+202=24S=√p(p−a)(p−b)(p−c)=√24(24−12)(24−16)(24−20)=√24.12.8.4=96(dvdt)
- Tính ha: Ta có:
S=12aha⇔96=12.12.ha⇔96=6.ha⇔ha=966=16
- Tính R
Ta có: S=abc4R⇔R=abc4S=12.16.204.96=10
- Tính r
Ta có: S=p.r⇔r=Sp=9624=4
- Tính ma. Ta có:
ma2=2(b2+c2)−a24=2(162+202)−1224=292⇔ma=√292≈17,09
1.11. Giải bài 11 trang 62 SGK Hình học 10
Trong tập hợp các tam giác có hai cạnh là a và b. Tìm tam giác có diện tích lớn nhất.
Phương pháp giải
Sử dụng công thức tính diện tích tam giác S=12absinC
Hướng dẫn giải
Theo công thức tính diện tích tam giác, ta có: S=12absinC
Ta có:
0<sinC≤1 ⇒0<12absinC≤12ab.1 ⇒0<S≤12ab
Mà ab không đổi nên S đạt GTLN bằng 12ab khi sinC=1 ⇔C=900
Vậy trong tập hợp các tam giác có hai cạnh a và b không đổi thì tam giác vuông đỉnh C có diện tích lớn nhất.
2. Câu hỏi trắc nghiệm
2.1. Giải bài 1 trang 63 SGK Hình học 10
Trong các đẳng thức sau đây, đẳng thức nào đúng?
A. sin1500=−√32
B. cos1500=√32
C. tan1500=−1√3
D. cot1500=√3
Phương pháp giải
Nếu 900<α<1800 thì sinα>0 còn các giá trị lượng giác khác của α đều nhận giá trị âm.
Hướng dẫn giải
Do 00<1500<1800 nên sin1500>0 (loại A)
cos1500<0 (loại B)
tan1500<0 và cot1500<0 (loại D).
Chọn C.
2.2. Giải bài 2 trang 63 SGK Hình học 10
Cho α và β là hai góc khác nhau và bù nhau. Trong các đẳng thức sau đây, đẳng thức nào sai?
A. sinα=sinβ
B. cosα=−cosβ
C. tanα=−tanβ
D. cotα=cotβ
Phương pháp giải
Hai góc bù nhau (α và π−α)
sin(π−α)=sinαcos(π−α)=−cosαtan(π−α)=−tanαcot(π−α)=−cotα
Hướng dẫn giải
sinα=sin(1800−α)=sinβ nên A đúng.
cosα=−cos(1800−α)=−cosβ nên B đúng.
tanα=−tan(1800−α)=−tanβ nên C đúng.
cotα=−cot(1800−α)=−cotβ nên D sai.
Vậy chọn D.
2.3. Giải bài 3 trang 63 SGK Hình học 10
Cho α là góc tù. Điều khẳng định nào sau đây là đúng?
A. sinα<0
B. cosα>0
C. tanα<0
D. cotα>0
Hướng dẫn giải
Khi 900<α<1800 thì: sinα>0 còn các giá trị lượng giác khác của α đều nhận giá trị âm.
Chọn C.
2.4. Giải bài 4 trang 63 SGK Hình học 10
Trong các khẳng định sau đây, khẳng định nào sai?
A. cos450=sin450
B. cos450=sin1350
C. cos300=sin1200
D. sin600=cos1200
Hướng dẫn giải
Chọn D vì: {sin600>0cos1200<0
2.5. Giải bài 5 trang 63 SGK Hình học 10
Hai góc nhọn α và β trong đó α<β . Khẳng định nào sau đây là sai?
A. cosα<cosβ
B. sinα<sinβ
C. α+β=900⇒cosα=sinβ
D. tanα+tanβ>0
Phương pháp giải
Vẽ đường tròn lượng giác để xác định các giá trị lượng giác của α rồi so sánh.
Hướng dẫn giải
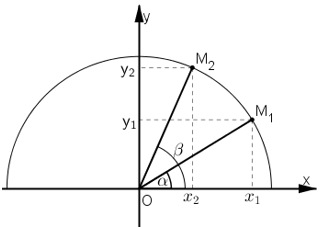
Biểu diễn góc α, β (α < β) trên nửa đường tròn lượng giác nằm phía trên trục hoành.
Ta có sin α = y1; cos α = x1 ; sin β = y2; cos β = x2.
x1 > x2 nên cos α > cos β
A sai.
y1 < y2 nên sin α < sin β.
B đúng
α + β = 90º ⇒ cos α = sin β.
C đúng
tan α > 0, tan β > 0 nên tan α + tan β > 0.
D đúng.
Chọn A.
2.6. Giải bài 6 trang 63 SGK Hình học 10
Tam giác ABC vuông ở A và có góc B=300. Khẳng định nào sau đây là sai?
A. cosB=1√3
B. sinC=√32
C. cosC=12
D. sinB=12
Phương pháp giải
Tính số đo góc C.
Sử dụng bảng số đo lượng giác của các góc đặc biệt:
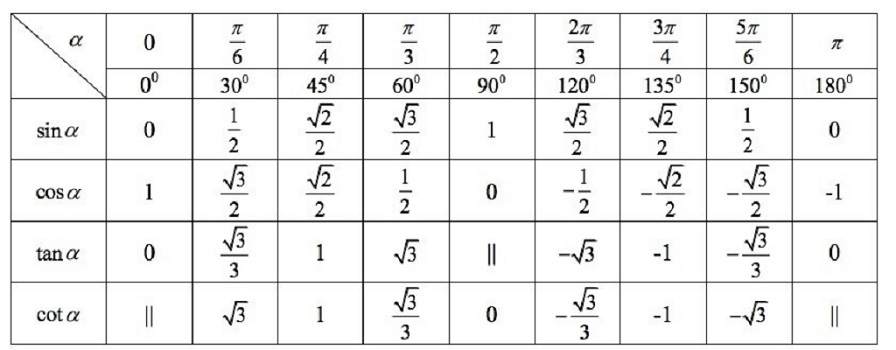
Hướng dẫn giải
B+C=900⇒C=900−B=900−300=600cosB=cos300=√32⇒AsaisinC=sin600=√32⇒BđúngcosC=cos600=12⇒CđúngsinB=sin300=12⇒Dđúng
Chọn A.
2.7. Giải bài 7 trang 63 SGK Hình học 10
Tam giác đều ABC có đường cao AH. Khẳng định nào sau đây là đúng?
A. sin^BAH=√32
B. cos^BAH=1√3
C. sin^ABC=√32
D. sin^AHC=12
Phương pháp giải
- Tam giác đều có mỗi góc bằng 60 độ.
- Tam giác ABC đều nên AH vừa là đường cao vừa là đường phân giác góc A. Từ đó tính được ^BAH
- Tính các giá trị lượng giác của các góc đã biết số đo.
Hướng dẫn giải
Tam giác ABC đều nên AH vừa là đường cao vừa là đường phân giác góc A.
⇒^BAH=12^BAC=12.600=300⇒sin^BAH=sin300=12⇒Asaicos^BAH=cos300=√32⇒Bsaisin^ABC=sin600=√32⇒Cđúngsin^AHC=sin900=1⇒Dsai
Chọn C
2.8. Giải bài 8 trang 64 SGK Hình học 10
Khẳng định nào sau đây là đúng?
A. sinα=sin(1800–α)
B. cosα=cos(1800–α)
C. tanα=tan(1800–α)
D. cotα=cot(1800–α)
Hướng dẫn giải
A đúng vì: Với hai góc bù sau thì có sin bằng nhau, còn các giá trị lượng giác khác là đối nhau.
2.9. Giải bài 9 trang 64 SGK Hình học 10
Tìm khẳng định sai trong các khẳng định sau đây:
A) cos350>cos100
B) sin600<sin800
C) tan450<tan600
D) cos450=sin450
Hướng dẫn giải
Với hai góc α và β thỏa mãn 0º < α < β < 90º ta luôn có:
cos α > cos β; sin α < sin β; tan α < tan β ; cot α > cot β
Chọn A.
2.10. Giải bài 10 trang 64 SGK Hình học 10
Tam giác ABC vuông ở A và có góc B=500. Hệ thức nào sau đây là sai:
A. (→AB,→BC)=1300
B. (→BC,→AC)=400
C. (→AB,→CB)=500
D. (→AC,→CB)=1200
Phương pháp giải
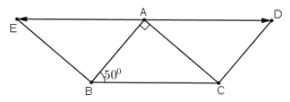
Dựng các véc tơ:
→AE=→CB,→AD=→BC ta có:
(→AB,→BC)=(→AB,→AD)=^BAD
- Tính được các góc dựa vào tam giác vuông.
Hướng dẫn giải
Mà AD//BC
⇒^BAD+^ABC=1800⇒^BAD=1800−^ABC=1800−500=1300
⇒(→AB,→BC)=1300
A đúng.
(→BC,→AC)=(→AD,→AC)=^CAD
Mà AD//BC nên
^CAD=^ACB=900−^ABC=900−500=400⇒(→BC,→AC)=400
B đúng.
(→AB,→CB)=(→AB,→AE)=^BAE
Mà AE//BC nên
^BAE=^ABC=500⇒(→AB,→CB)=500
C đúng.
(→AC,→CB)=(→AC,→AE)=^CAE
Mà AE//BC nên
^CAE+^ACB=1800⇒^CAE=1800−^ACB=1800−400=1400⇒(→AC,→CB)=^CAE=1400
D sai.
2.11. Giải bài 11 trang 64 SGK Hình học 10
Cho →a và →b là hai vecto cùng hướng và đều khác vecto →0. Trong các kết quả sau đây, hãy chọn kết quả đúng.
A. →a.→b=|→a|.|→b|
B. →a.→b=0
C. →a.→b=−1
D. →a.→b=−|→a|.|→b|
Hướng dẫn giải
→a.→b=|→a|.|→b|cos(→a,→b)
Khi →a và →b cùng hướng thì (→a,→b)=00
cos(→a,→b)=1⇒→a.→b=|→a|.|¯b|
Chọn A.
2.12. Giải bài 12 trang 64 SGK Hình học 10
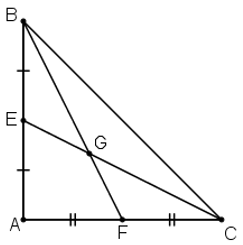
Cho tam giác ABC vuông cân tại A có AB=AC=30cm. Hai đường trung tuyến BF và CE cắt nhau tại G. Diện tích tam giác GFC là:
A. 50cm2
B. 50√2cm2
C. 75cm2
D. 15√105cm2
Phương pháp giải
- Tính tỉ lệ diện tích các tam giác vuông theo tỉ lệ của cạnh đáy có chung đường cao.
- Sử dụng tính chất chất trọng tâm của tam giác cách các đỉnh của tam giác một đoạn bằng 2/3 độ dài đường trung tuyến ứng với đỉnh đó.
Hướng dẫn giải
G là trọng tâm tam giác ABC nên FG = 1/3.BF
⇒ SGFC=13SBFC
F là trung điểm của AC nên FC = 1/2. AC
SBFC=12SBAC
⇒SGFC=13SBFC=13.12SBAC=16SBAC=16.12.AB.AC=16.12.30.30=75(cm2)⇒SGFC=75(cm2)
Chọn C.
2.13. Giải bài 13 trang 64 SGK Hình học 10
Cho tam giác ABC vuông tại A có AB=5cm,BC=13cm. Gọi góc ABC=α và góc ACB=β. Hãy chọn kết luận đúng khi so sánh α và β.
A) β>α B) β<α
C) α=β D) α≤β
Phương pháp giải
Sử dụng định lý Py-ta-go cho tam giác vuông tính được cạnh AC.
Sử dụng quan hệ giữa góc và cạnh đối diện: Trong một tam giác góc đối diện cạnh lớn hơn thì lớn hơn.
Hướng dẫn giải
Tam giác ABC vuông tại A nên theo Py-ta-go ta có:
AB2+AC2=BC2 ⇔AC2=BC2−AB2 =132−52=144
⇒AC=12
Mà AC>AB⇒^ABC>^ACB ⇒α>β (góc đối diện với cạnh lớn hơn thì lớn hơn)
Chọn B.
2.14. Giải bài 14 trang 64 SGK Hình học 10
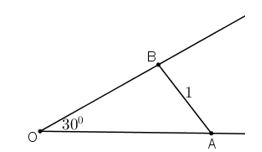
Cho góc xOy=300. Gọi A và B là hai điểm di động lần lượt trên Ox và Oy sao cho AB=1. Độ dài lớn nhất của đoạn OB bằng:
A. 1,5 B. √3
C. 2√2 D. 2
Phương pháp giải
- Độ dài OB lớn nhất khi OB là cạnh huyền của tam giác OAB vuông tại A.
- Dử dụng định lí sin để đánh giá.
Hướng dẫn giải
Áp định lí sin trong tam giác AOB ta có:
OBsin^OAB=ABsin^AOB⇒OBsin^OAB=112=2⇒OB=2sin^OAB
Vì sin^OAB≤1 nên OB=2sin^OAB≤2
⇒OB đạt giá trị lớn nhất là 2 khi sin^OAB=1
⇒^OAB=900 hay AB⊥Ox
Vậy OB lớn nhất bằng 2.
Vậy chọn D.
2.15. Giải bài 15 trang 65 SGK Hình học 10
Cho tam giác ABC có BC=a,CA=b,AB=c. Mệnh đề nào sau đây là đúng?
A. Nếu b2+c2−a2>0 thì góc A nhọn
B. Nếu b2+c2−a2>0 thì góc A tù.
C. Nếu b2+c2−a2<0 thì góc A nhọn.
D. Nếu b2+c2−a2>0 thì góc A vuông.
Phương pháp giải
- Sử dụng định lí cosin để đánh giá.
- Đánh giá b2+c2−a2 dựa vào cosA.
Hướng dẫn giải
Áp dụng định lý Côsin trong tam giác ABC ta có: cosA=b2+c2−a22bc
Nếu b2+c2−a2>0 thì cosA>0⇔A<900 ⇒ˆA là góc nhọn.
Nếu b2+c2−a2<0 thì cosA<0⇔A>900 ⇒ˆA là góc tù.
Chọn A.
2.16. Giải bài 16 trang 65 SGK Hình học 10
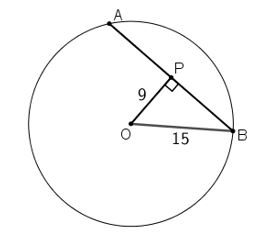
Đường tròn tâm O bán kính R=15cm. Gọi P là một điểm cách tâm O một khoảng PO=9cm. Dây cung đi qua P và vuông góc với PO có độ dài là:
A. 22cm B. 23cm
C. 24cm D. 25cm
Phương pháp giải
- Sử dụng tính chất: Đường kính vuông góc với dây cung thì đi qua trung điểm của dây cung đó.
- Áp dụng định lí Py-ta-go tính được PB rồi suy ra AB.
Hướng dẫn giải
Gọi dây cung vuông góc với OP tại P là MN.
Khi đó OP⊥MN⇒P là trung điểm MN (đường kính vuông góc với dây cùng thì đi qua trung điểm của dây)
Áp dụng định lý pitago trong tam giác OPM ta có:
PM2=OM2−OP2=152−92=225−81=144⇒PM=12⇒MN=2PM=2.12=24
Chọn C.
2.17. Giải bài 17 trang 65 SGK Hình học 10
Cho tam giác ABC có AB=8cm,AC=18cm và có diện tích bằng 64cm2. Giá trị sinA là:
A. √32 B. 38
C. 45 D. 89
Phương pháp giải
- Áp dụng công thức tính diện tích S=12AB.AC.sinA để suy ra sinA.
Hướng dẫn giải
Áp dụng công thức: S=12AB.AC.sinA
⇒sinA=2SAB.AC=2.648.18=89
Do đó chọn D
2.18. Giải bài 18 trang 65 SGK Hình học 10
Cho hai góc nhọn α và β phụ nhau. Hệ thức nào sau đây là sai?
A. sinα=−cosβ
B. cosα=sinβ
C. tanα=cotβ
D. cotα=tanβ
Phương pháp giải
Nếu có α + β = 90º thì:
sin α = cos β ; cos α = sin β;
tan α = cot β; cot α = tan β.
Hướng dẫn giải
A sai
Chọn A.
2.19. Giải bài 19 trang 65 SGK Hình học 10
Bất đẳng thức nào dưới đây là đúng?
A. sin900<sin1500
B. sin90015′<sin90030′
C. cos90030′>cos1000
D. cos1500>cos1200
Phương pháp giải
- Các giá trị lượng giác đặc biệt thì tính được.
- Sử dụng tính chất sin a = sin (180º-a).
Hướng dẫn giải
sin 90º = 1, sin 150º = 1/2
⇒ sin 90º > sin 150º (A sai)
sin 90º15’ = sin 89º45’;
sin 90º30’ = sin 89º30’.
Mà với 0º < α < β < 90º thì sin α < sin β
⇒ sin 89º45’ > sin 89º30’
⇒ sin 90º15’ > sin 90º30’ (B sai)
Với 0º < α < β < 180º thì cos α > cos β
⇒ cos 90º30’ > cos 100º (C đúng)
cos 150º = –√3/2, cos 120º = –1/2 nên cos 150º < cos 120º (D sai)
Chọn C.
2.20. Giải bài 20 trang 65 SGK Hình học 10
Cho tam giác ABC vuông tại A. Khẳng định nào dưới đây là sai?
A. →AB.→AC<→BA.→BC
B. →AC.→CB<→AC.→BC
C. →AB.→BC<→CA.→CB
D. →AC.→BC<→BC.→AB
Phương pháp giải
- Từ công thức →a.→b=|a|.|b|.Cos(→a,→b) ta so sánh tích vô hướng của các vectơ với 0 dựa vào giá trị của Cos(→a,→b).
Hướng dẫn giải
→AB⊥→AC nên →AB.→AC=0
(→AB,→AC)=^ABC=90∘⇒cos(→BA,→BC)>0⇒→BA.→BC=BA.BC>cos(→BA,→BC)>0⇒→AB.→AC<→BA.→BC(→AC,→CB)=180∘−^ACB>90∘⇒cos(→AC,→CB)<0⇒→AC.→CB<0
(→AC,→BC)=^ACB<90∘⇒cos(→AC,→BC)>0⇒→AC.→BC>0
Do đó: →AC.→CB<→AC.→BC
→AC.→AC=0(→CA;→CB)=^ACB<90∘⇒cos(→CA;→CB)>0⇒→CA.→CB>0
Do đó: →AB.→AC<→CA.→CB
(→AC;→BC)=^ACB<90∘⇒cos(→AC;→BC)>0⇒→AC.→BC>0(→BC;→AB)=180∘−^ABC>90∘⇒cos(→BC;→AB)<0→BC;→AB<0
Do đó: →AC.→BC<→BC.→AB
2.21. Giải bài 21 trang 65 SGK Hình học 10
Tam giác ABC có AB=4cm,BC=7cm,CA=9cm. Giá trị của cosA là:
A. 23 B. 13
C. −23 D. 12
Phương pháp giải
Sử dụng hệ quả của định lí cosin: cosA=b2+c2−a22bc
Hướng dẫn giải
Sử dụng hệ quả của định lí cosin:
cosA=AB2+AC2−BC22AB.AC
=42+92−722.9.4=23
Chọn A.
2.22. Giải bài 22 trang 65 SGK Hình học 10
Cho hai điểm A(1;2) và B(3;4). Giá trị của →AB2 là:
A. 4 B. 4√2
C . 6√2 D. 8
Phương pháp giải
- Tính tọa độ →AB
- Tính →AB2.
Hướng dẫn giải
Ta có: →AB=(3−1;4−2)=(2,2)
⇒→AB2=22+22=8
Chọn D.
2.23. Giải bài 23 trang 66 SGK Hình học 10
Cho hai vecto →a=(4;3) và →b=(1;7). Góc giữa hai vecto →a và →b là:
A. 900 B. 600
C. 450 D. 300
Phương pháp giải
Sử dụng công thức cosin của hai góc giữa hai vecto:
cos(→a,→b)=→a.→b|→a|.|→b| =a1b1+a2b2√a12+a22√b12+b22
Hướng dẫn giải
Với →a=(4,3) ; và →b=(1,7) và ta có:
cos(→a,→b)=4.1+3.7√42+32.√12+72=√22
Góc giữa hai vecto →a và →b là: 450
Chọn C.
2.24. Giải bài 24 trang 66 SGK Hình học 10
Cho hai điểm M=(1;−2) và N=(−3;4). Khoảng cách giữa hai điểm M và N là:
A. 4 B. 6
C. 3√6 D. 2√13
Phương pháp giải
Sử dụng công thức khoảng cách giữa hai điểm: Với A(a1;a2);B(b1;b2) thì
AB=√(b1−a1)2+(b2−a2)2
Hướng dẫn giải
MN=√(−3−1)2+(4−(−2))2=√52=2√13
Chọn D.
2.25. Giải bài 25 trang 66 SGK Hình học 10
Tam giác ABC có A=(−1;1);B=(1;3) và C=(1;−1)
Trong các cách phát biểu sau đây, hãy chọn cách phát biểu đúng.
A. ABC là tam giác có ba cạnh bằng nhau
B. ABC là tam giác có ba góc đều nhọn
C. ABC là tam giác cân tại B (có BA=BC)
D. ABC là tam giác vuông cân tại A.
Phương pháp giải
Tính các cạnh AB, AC, BC theo công thức AB=√(xB−xA)2+(yB−yA)2 và nhận xét.
Hướng dẫn giải
Ta có:
AB=√(1−(−1))2+(3−1)2=√22+22=2√2AC=√(1−(−1))2+(−1−1)2=√22+22=2√2BC=√(1−1)2+(−1−3)2=√02+(−4)2=4⇒AB=AC
Suy ra tam giác ABC cân tại A (1)
Mà
AB2+AC2=(2√2)2+(2√2)2=16BC2=42=16⇒AB2+AC2=BC2
Theo định lý Pitago đảo suy ra tam giác ABC vuông tại A (2)
Từ (1) và (2) suy ra tam giác ABC vuông cân tại A.
Chọn D.
2.26. Giải bài 26 trang 66 SGK Hình học 10
Tam giác ABC có A=(10;5),B=(3;2),C=(6;−5). Khẳng định nào sau đây là đúng?
A. ABC là tam giác đều
B. ABC là tam giác vuông cân tại B
C. ABC là tam giác vuông cân tại A
D. ABC là tam giác có góc tù tại A.
Phương pháp giải
Tính các cạnh AB, AC, BC theo công thức AB=√(xB−xA)2+(yB−yA)2 và nhận xét.
Hướng dẫn giải
AB=√(3−10)2+(2−5)2=√58AC=√(6−10)2+(−5−5)2=√116BC=√(6−3)2+(−5−2)2=√58
Ta thấy,
AB=BC nên tam giác ABC cân tại B.
Lại có
AB2+BC2=(√58)2+(√58)2=116AC2=(√116)2=116⇒AB2+BC2=AC2
Do đó tam giác ABC vuông tại B.
Vậy tam giác ABC vuông cân tại B.
Chọn B.
2.27. Giải bài 27 trang 66 SGK Hình học 10
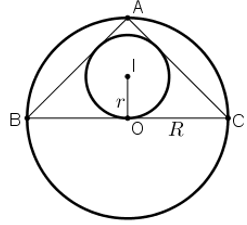
Tam giác ABC vuông cân tại A và nội tiếp trong đường tròn tâm O bán kính R. Gọi r là bán kính đường tròn nội tiếp tam giác ABC. Khi đó tỉ số Rr là:
A. 1+√2
B. 2+√22
C. √2−12
D. 1+√22
Phương pháp giải
- Tính bán kính R.
- Tính diện tích tam giác và nửa chu vi suy ra r.
- Tính tỉ số.
Hướng dẫn giải
Đặt AB=AC=a.
Tam giác ABC vuông tại A nên theo Pitago ta có: BC=AB2+AC2 =√a2+a2=a√2
⇒R=12BC=a√22.
Nửa chu vi tam giác ABC là: p=a+a+a√22 =2a+a√22
Ta có: SABC=12AB.AC=12.a.a=a22
Mà SABC=pr
⇒r=SABCp=a222a+a√22 =a22:2a+a√22=a22.22a+a√2=a2+√2
⇒Rr =a√22a2+√2
=a√22:a2+√2=a√22.2+√2a =√2(2+√2)2=√2+1
Vậy chọn A.
2.28. Giải bài 28 trang 66 SGK Hình học 10
Tam giác ABC có AB=9cm,AC=12cm,BC=15cm. Khi đó đường trung tuyến AM của tam giác có độ dài là:
A. 8cm B. 10cm
C. 9cm D. 7,5cm
Phương pháp giải
Áp dụng công thức trung tuyến
m2a=2(b2+c2)−a24
Hướng dẫn giải
Ta có:
AM2=2(AB2+AC2)−BC24=2(92+122)−1524=2254⇒AM=√2254=152=7,5(cm)
Chọn D
2.29. Giải bài 29 trang 67 SGK Hình học 10
Tam giác ABC có BC=a,CA=b,AB=c và có diện tích S. Nếu tăng cạnh BC lên 2 lần đồng thời tăng cạnh CA lên 3 lần và giữ nguyên độ lớn của góc C thì khi đó diện tích tam giác mới được tạo nên bằng:
A. 2S B. 3S
C. 4S D. 6S.
Phương pháp giải
Sử dụng công thức tính diện tích S=12absinC
Hướng dẫn giải
Ta có: S=12absinC
Khi tăng cạnh BC lên 2 lần ta được a′=2a.
Tăng cạnh CA lên 3 lần ta được b′=3b.
Giữ nguyên độ lớn góc C nên sinC′=sinC.
Vậy S′=12a′b′sinC′=12.2a.3b.sinC =6.12absinC=6S
Vậy chọn D
2.30. Giải bài 30 trang 67 SGK Hình học 10
Cho tam giác DEF có DE=DF=10cm và EF=12cm. Gọi I là trung điểm của cạnh EF. Đoạn thẳng DI có độ dài là:
A. 6,5cm B. 7cm
C. 8cm D. 4cm
Phương pháp giải
Áp dụng công thức tính độ dài đường trung tuyến
m2a=2(b2+c2)−a24
Hướng dẫn giải
Ta có: DI là đường trung tuyến của tam giác DEF
Áp dụng công thức tính độ dài đường trung tuyến:
DI2=2(DE2+DF2)−EF24=2(102+102)−1224=64⇒DI=√64=8cm
Vậy chọn C.
Tham khảo thêm
- doc Giải bài tập SGK Toán 10 Chương 2 Bài 1: Giá trị lượng giác của một góc bất kỳ từ 0 độ đến 180 độ
- doc Giải bài tập SGK Toán 10 Chương 2 Bài 2: Tích vô hướng của hai vectơ
- doc Giải bài tập SGK Toán 10 Chương 2 Bài 3: Các hệ thức lượng trong tam giác và giải tam giác