Giải bài tập SGK Toán 10 Chương 2 Bài 1: Giá trị lượng giác của một góc bất kỳ từ 0 độ đến 180 độ
Phần hướng dẫn giải bài tập Bài Giá trị lượng giác của một góc bất kỳ từ 0 độ đến 180 độ sẽ giúp các em nắm được phương pháp và rèn luyện kĩ năng các giải bài tập từ SGK Toán 5. Hi vọng rằng đây sẽ là những tài liệu hữu ích trong công tác giảng dạy và học tập của quý thầy cô và các em học sinh.
Mục lục nội dung

Giải bài tập SGK Toán 10 Chương 2 Bài 1: Giá trị lượng giác của một góc bất kỳ từ 0 độ đến 180 độ
1. Giải bài 1 trang 40 SGK Hình học 10
Chứng minh rằng trong tam giác ABC ta có:
a) sinA=sin(B+C); b) cosA=−cos(B+C)
Phương pháp giải
Câu a
Tổng ba góc trong tam giác bằng 1800.
Sử dụng công thức sinα=sin(1800−α) với α=A
Câu b
Sử dụng công thức cosα=−cos(1800−α) với α=A
Hướng dẫn giải
Câu a
Ta có: A+B+C=1800 ⇒B+C=1800−A
Do đó: sinA=sin(1800−A)=sin(B+C)
Cách trình bày khác:
sinA=sin[1800−(B+C)]
=sin(B+C).
Câu b
Ta có: A+B+C=1800 ⇒B+C=1800−A
Khi đó: cosA=−cos(1800−A) =−cos(B+C)
Cách trình bày khác:
cosA=cos[1800−(B+C)]=−cos(B+C).
2. Giải bài 2 trang 40 SGK Hình học 10
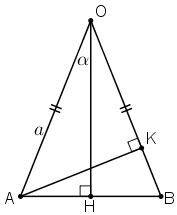
Cho AOB là tam giác cân tại O có OA=a và có các đường cao OH và AK. Giả sử ^AOH=α. Tính AK và OK theo a và α.
Phương pháp giải
+) Sử dụng công thức lượng giác đối với góc nhọn ta có: sinα=cạnhđốicạnhhuyền và cosα=cạnhkềcạnhhuyền
Hướng dẫn giải
Do tam giác OAB cân tại O nên ta có ^AOB=2^AOH=2α<900
Tam giác OKA vuông tại K nên ta có:
sin^AOK=AKOA
⇒AK=OA.sin^AOK⇒AK=a.sin2α.
cos^AOK=OKOA
⇒OK=OA.cos^AOK⇒OK=a.cos2α.
3. Giải bài 3 trang 40 SGK Hình học 10
Chứng minh rằng:
a) sin1050=sin750;
b) cos1700=−cos100;
c) cos1220=−cos580
Phương pháp giải
Câu a
Sử dụng công thức lượng giác: sinα=sin(1800−α)
Câu b
Sử dụng công thức lượng giác:cosα=−cos(1800−α)
Câu d
Sử dụng công thức lượng giác:cosα=−cos(1800−α)
Hướng dẫn giải
Câu a
sin1050=sin(1800−1050).
(áp dụng công thức sinα=sin(1800−α) với α=1050)
⇒sin1050=sin750.
Câu b
cos1700=−cos(1800−1700).
(áp dụng công thức cosα=−cos(1800−α) với α=1700)
⇒cos1700=−cos100.
Câu c
cos1220=−cos(1800−1220).⇒cos1220=−cos580.
(áp dụng công thức cosα=−cos(1800−α) với α=1220)
4. Giải bài 4 trang 40 SGK Hình học 10
Chứng minh rằng với mọi góc α(00≤α≤1800) ta đều có sin2α+cos2α=1.
Hướng dẫn giải
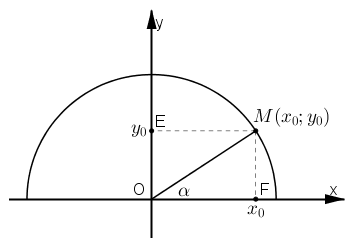
Vẽ nửa đường tròn lượng giác (O; 1).
Với mọi α (0º ≤ α ≤ 180º) ta đều có điểm M(x0; y0) thuộc nửa đường tròn sao cho ^xOM=α
Khi đó ta có: sin α = y0 ; cos α = x0.
Mà M thuộc đường tròn lượng giác nên OM=1.
Ta có:
sin2α+cos2α=y20+x20=OE2+OF2=MF2+OF2=OM2=12=1⇒sin2α+cos2α=1
5. Giải bài 5 trang 40 SGK Hình học 10
Cho góc x, với cosx=13. Tính giá trị của biểu thức: P=3sin2x+cos2x.
Phương pháp giải
Áp dụng công thức: sin2x+cos2x=1.
Hướng dẫn giải
Ta có: sin2x+cos2x=1 ⇒sin2x=1−cos2x.
Do đó P=3sin2x+cos2x=3(1−cos2x)+cos2x
=3−3cos2x+cos2x
=3−2cos2x
=3−2.(13)2=259.
Cách trình bày khác:
sin2x+cos2x=1⇒sin2x=1−cos2x=1−(13)2=89⇒P=3sin2x+cos2x=3.89+(13)2=259
6. Giải bài 6 trang 40 SGK Hình học 10
Cho hình vuông ABCD. Tính: cos(→AC,→BA),sin(→AC,→BD),cos(→AB,→CD).
Phương pháp giải
Cho hai vecto →a,→b(khác→0). Từ một điểm O bất kì ta vẽ →OA=→a,→OB=→b.
Khi đó ^AOB với số đo từ 00 đến 1800 được gọi là góc giữa hai vecto →a,→b.
Kí hiệu: (→a,→b).
Hướng dẫn giải
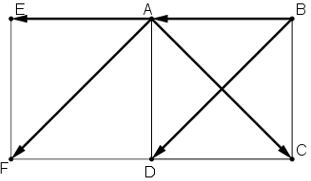
+) Dựng →AE=→BA ta có :
(→AC,→BA)=(→AC,→AE)=^CAE
Mà ABCD là hình vuông nên ^BAC=450
⇒^CAE=1800−^BAC =1800−450=1350
⇒cos(→AC,→BA)=cos1350=cos(1800−450)=−cos450=−1√2
Vậy cos(→AC,→BA)=−1√2
- Dựng →AF=→BD ta có: (→AC,→BD)=(→AC,→AF)=^CAF
Mà →AF=→BD nên AF//BD.
Lại có AC ⊥ BD nên AC ⊥ AF hay ^CAF=900.
Vậy cos(→AC,→BD) =cos^CAF=cos900=0
- Vì →AB,→CD là hai véc tơ ngược hướng nên:
(→AB,→CD)=1800 ⇒cos(→AB,→CD)=cos1800=−1
Tham khảo thêm
- doc Giải bài tập SGK Toán 10 Chương 2 Bài 2: Tích vô hướng của hai vectơ
- doc Giải bài tập SGK Toán 10 Chương 2 Bài 3: Các hệ thức lượng trong tam giác và giải tam giác
- doc Giải bài tập SGK Toán 10 Ôn tập chương 2: Tích vô hướng của hai vectơ và ứng dụng