Giải bài tập SBT Vật Lí 12 Bài tập cuối chương 3: Dòng điện xoay chiều

Khi đặt một hiệu điện thế không đổi 12V vào hai đầu một cuộn dây có điện trở thuần R và độ tự cảm L thì dòng điện qua cuộn dây là dòng điện một chiều có cường độ 0,15A. Nếu đặt vào hai đầu cuộn dây này một điện áp xoay chiều có giá trị hiệu dụng 100V thì cường độ hiệu dụng qua nó là 1A. Cảm kháng của cuộn dây bằng

A. 60Ω.                            B. 40Ω.

C. 50Ω.                            D. 30Ω.

Phương pháp giải

- Tính điện trở bằng công thức: R = U/I

- Áp dụng định luật Ôm: I=U/Z để tìm Z: Z=U/I

- Áp dụng công thức tính tổng trở: 

\(Z = \sqrt {{R^2} + {Z_L}^2} \)

Hướng dẫn giải

- Chỉ có điện trở cản trở dòng điện không đổi:

\(R = \frac{{{U_{1c}}}}{{{I_{1c}}}} = \frac{{12}}{{0,15}} = 80{\rm{\Omega }}\)

- Mạch xoay chiều ta có: 

I=U/Z ⇒ Z = U/I = 100/1 = 100Ω

- Tổng trở của mạch điện:

\(\begin{array}{l} Z = \sqrt {{R^2} + {Z_L}^2} \\ \Rightarrow {Z_L} = \sqrt {{Z^2} - {R^2}} = \sqrt {{{100}^2} - {{80}^2}} = 60{\rm{\Omega }} \end{array}\)

-Chọn A

Một đoạn mạch điện RLC nối tiếp có U_R= UC= 0,5U_L. So với cường độ dòng điện thì điện áp giữa hai đầu đoạn mạch này

A. Trễ pha π/2.           

B. Sớm pha π/4.

C. Lệch pha π/2.             

D. Sớm pha π/3.

Phương pháp giải

- Vận dụng công thức:

\(\varphi = {\varphi _u} - {\varphi _i};\,\,\tan \varphi = \frac{{{U_L} - {U_C}}}{{{U_R}}}\)

 để tính độ lệch pha giữa điện áp và dòng điện

- So với cường độ dòng điện thì điện áp giữa hai đầu đoạn mạch này sớm pha π/4

Hướng dẫn giải

- Ta có: 

U_R= U_C= 0,5U_L

U_L= 2U_R

- Độ lệch pha giữa điện áp và dòng điện là φ

- Xét

\(\begin{array}{*{20}{l}} {\tan \varphi = \frac{{{U_L} - {U_C}}}{{{U_R}}} = \frac{{2{U_R} - {U_R}}}{{{U_R}}} = 1}\\ { \Rightarrow \varphi = \frac{\pi }{4} = {\varphi _u} - {\varphi _i} > 0 \Rightarrow {\varphi _u} > {\varphi _i}} \end{array}\)

- So với cường độ dòng điện thì điện áp giữa hai đầu đoạn mạch này sớm pha π/4.

- Chọn B

Đặt điện áp xoay chiều u=U₀cos100πt(V) vào hai đầu đoạn mạch AB mắc nối tiếp gồm điện trở thuần 100Ω, tụ điện có điện dung 10⁻⁴π(F) và cuộn cảm thuần có độ tự cảm thay đổi được. Để điện áp hai đầu điện trở trễ pha π/4 so với điện áp hai đầu đoạn mạch AB thì độ tự cảm của cuộn cảm bằng

A. 1/5π(H).                       B. 1/2π(H).

C. 10⁻²/2π(H).                 D. 2/π(H).

Phương pháp giải

- Tính dung kháng theo công thức:

\({Z_C} = \frac{1}{{C\omega }}\)

- Áp dụng công thức 

\(\varphi = {\varphi _u} - {\varphi _i};\,\,\tan \varphi = \frac{{{U_L} - {U_C}}}{{{U_R}}}\)

để tính độ lệch pha giữa điện áp và dòng điện

- Dòng điện trễ pha π/4 so với điện áp hai đầu đoạn mạch AB

⇒ φ = π/4 rad

Hướng dẫn giải

- Dung kháng:

\({Z_C} = \frac{1}{{C\omega }} = \frac{1}{{\frac{{{{10}^{ - 4}}}}{\pi }.100\pi }} = 100({\rm{\Omega }})\)

- Điện áp giữa hai đầu điện trở cùng pha với dòng điện, điện áp hai đầu điện trở trễ pha π/4 so với điện áp hai đầu đoạn mạch AB nên dòng điện cũng trễ pha π/4 so với điện áp hai đầu đoạn mạch AB

⇒ φ = π/4 rad

\(\begin{array}{*{20}{l}} {\tan \varphi = \frac{{{Z_L} - {Z_C}}}{R}}\\ { \Leftrightarrow \tan (\frac{\pi }{4}) = \frac{{{Z_L} - 100}}{{100}}}\\ { \Rightarrow {Z_L} = 200{\rm{\Omega }}} \end{array}\)

- Ta có cảm kháng: Z_L =Lω 

⇒L= Z_Lω=200/100π= 2/π(H)

- Chọn D

Đặt điện áp xoay chiều có tần số 50Hz vào hai đầu một đoạn mạch gồm một cuộn cảm thuần có độ tự cảm 0,2H và một tụ điện có điện dung 10μF mắc nối tiếp. Độ lệch pha của điện áp giữa hai đầu đoạn mạch so với cường độ dòng điện trong mạch là

A. 0.                                      B. π/4.

C. −π/2.                                D. π/2.

Phương pháp giải

- Tính tần số góc: ω = 2πf 

- Tính cảm kháng: Z_L= Lω

- Áp dụng công thức 

\(\varphi = {\varphi _u} - {\varphi _i};\,\,\tan \varphi = \frac{{{U_L} - {U_C}}}{{{U_R}}}\)

để tính độ lệch pha giữa điện áp và dòng điện 

Hướng dẫn giải

- Tần số góc:

ω = 2πf = 2π.50= 100π (rad/s)

- Cảm kháng là:

Z_L= Lω= 0,2.100π= 20π(Ω)

- Dung kháng là:

\({Z_C} = \frac{1}{{C\omega }} = \frac{1}{{{{10.10}^{ - 6}}.100\pi }} = \frac{{1000}}{\pi }({\rm{\Omega }})\)

- Do mạch điện chỉ có tự và cuộn cảm thuần, Z_C>Z_L nên 

điện áp trễ pha hơn dòng điện góc π/2 ⇒ φ= −π/2 rad

- Chọn C

Đặt điện áp xoay chiều u=200√2cos100πt(V) vào hai đầu đoạn mạch gồm điện trở R, cuộn cảm thuần và tụ điện mắc nối tiếp thì cường độ dòng điện hiệu dụng trong đoạn mạch là √2A. Biết cảm kháng và dung kháng của đoạn mạch lần lượt là 200Ω và 100Ω. Giá trị của R là

A. 50Ω.                                 B. 400Ω.

C. 100Ω.                               D. 100√3Ω.

Phương pháp giải

- Áp dụng định luật Ôm: I= U/Z để tính Z: Z= U/I

- Vận dụng công thức tính tổng trở đoạn mạch:

\({Z = \sqrt {{R^2} + {{({Z_L} - {Z_C})}^2}} }\)

để tính R

Hướng dẫn giải

- Ta có:

I= U/Z ⇒ Z= U/I= 200/√2 = 100√2 Ω

\(\begin{array}{*{20}{l}} {Z = \sqrt {{R^2} + {{({Z_L} - {Z_C})}^2}} }\\ { \Leftrightarrow 100\sqrt 2 = \sqrt {{R^2} + {{(200 - 100)}^2}} }\\ { \Rightarrow R = 100{\rm{\Omega }}} \end{array}\)

- Chọn C

Đặt điện áp xoay chiều có giá trị hiệu dụng không đổi vào hai đầu một điện trở 100Ω. Công suất tỏa nhiệt trên điện trở là 100W. Cường độ hiệu dụng qua điện trở bằng

A. 2√2A.                        B. 1A.

C. 2A.                            D. √2A.

Phương pháp giải

Tính công suất tỏa nhiệt trên điện trở theo công thức:

P= I²R

Hướng dẫn giải

- Công suất tỏa nhiệt trên điện trở:

P=I²R ⇔ 100 =I².100 ⇒ I= 1A

- Chọn B

Đặt điện áp xoay chiều u=U₀cosωt vào hai đầu một đoạn mạch gồm điện trở R, cuộn cảm thuần có độ tự cảm L và tụ điện có điện dung C mắc nối tiếp. Hệ số công suất của đoạn mạch là:

\(\begin{array}{l} A.\,\,\frac{{\omega L - \frac{1}{{\omega C}}}}{R}.\\ B.\,\,\frac{R}{{\omega L - \frac{1}{{\omega C}}}}.\\ C.\,\,\frac{R}{{\sqrt {{R^2} + {{(\omega L - \frac{1}{{\omega C}})}^2}} }}.\\ D.\,\,\frac{R}{{\sqrt {{R^2} + {{(\omega L + \frac{1}{{\omega C}})}^2}} }}. \end{array}\)

Phương pháp giải

- Công thức tính hệ số công suất: cosφ = R/Z

- Tính tổng trở:

\({Z = \sqrt {{R^2} + {{({Z_L} - {Z_C})}^2}} }\)

- Áp dụng công thức tính dung kháng Z_C= 1/Cω,  cảm kháng Z_L= Lω

Hướng dẫn giải

- Hệ số công suất:

\(\begin{array}{l} \cos \varphi = \frac{R}{Z}\\ = \frac{R}{{\sqrt {{R^2} + {{({Z_L} - {Z_C})}^2}} }}\\ = \frac{R}{{\sqrt {{R^2} + {{(L\omega - \frac{1}{{C\omega }})}^2}} }} \end{array}\)

- Chọn C

Đặt điện áp u=U√2cos2πft (U không đổi, f thay đổi được) vào hai đầu  đoạn mạch R,L,C. Khi tần số là f₁ thì cảm kháng và dung kháng của đoạn mạch có giá trị lần lượt là 6Ω và 8Ω. Khi tần số là f₂ thì hệ số công suất của đoạn mạch R,L,C này bằng 1. Hệ thức liên hệ giữa f₁ và f₂ là

A. f₂= 2√3f₁.            B. f₂=√3/2f₁.

C. f₂= 4/3f₁.             D. f₂=3/4f₁.

Phương pháp giải

- Tính dung kháng Z_C= 1/(2πfC)

- Tính cảm kháng Z_L= 2πf.L

Suy ra mối liên hệ của f và các đại lượng trong công thức:

- Lập tỉ số khi Z_L=Z_C để tìm tỉ lệ của f

Hướng dẫn giải

- Khi f= f₁ có

+ Z_C= 1/(2πf₁C) = 8Ω

+ Z_L = 2πf₁L= 6Ω

\(\begin{array}{*{20}{l}} { \Rightarrow 4{\pi ^2}LCf_1^2 = \frac{3}{4}}\\ { \Rightarrow f_1^2 = \frac{3}{4}.\frac{1}{{4{\pi ^2}LC}}(1)} \end{array}\)

- Khi tần số là f= f₂ thì hệ số công suất của đoạn mạch RLC này bằng 1.

\(\begin{array}{*{20}{l}} {{Z_L} = {Z_C}}\\ { \Rightarrow 2\pi {f_2}L = \frac{1}{{2\pi {f_2}C}}}\\ { \Rightarrow f_2^2 = \frac{1}{{4{\pi ^2}LC}}(2)} \end{array}\)

- Từ (1)(2) 

\(f_1^2 = \frac{3}{4}f_2^2 \Rightarrow {f_2} = \frac{2}{{\sqrt 3 }}{f_1}\)

- Chọn A

Đặt điện áp u=U√2cosωt vào hai đầu đoạn mạch AB gồm hai đoạn mạch AN và NB mắc nối tiếp. Đoạn AN gồm biến trở R mắc nối tiếp với cuộn cảm thuần có độ tự cảm L, đoạn chỉ có tụ điện với điện dung C. Để điện áp hiệu dụng giữa hai đầu đoạn mạch AN không phụ thuộc R thì tần số góc ω phải bằng

\(\begin{array}{l} A.\,\,\frac{1}{{2\sqrt {2LC} }}.\\ B.\,\,\frac{1}{{4\sqrt {2LC} }}.\\ C.\,\,\frac{1}{{\sqrt {LC} }}.\\ D.\,\,\frac{1}{{\sqrt {2LC} }}. \end{array}\)

Phương pháp giải

- Áp dụng định luật Ôm: U = I.Z

- Điện áp hiệu dụng không phụ thuộc R được tính theo công thức:

\({\sqrt {{R^2} + {{({Z_L} - {Z_C})}^2}} = \sqrt {{R^2} + {Z_L}^2} }\)

Hướng dẫn giải

- Ta có

\(\begin{array}{*{20}{l}} {{U_{AN}} = {U_{RL}} = I.{Z_{RL}}}\\ { = \frac{U}{Z}.{Z_{RL}}}\\ { = \frac{U}{{\sqrt {{R^2} + {{({Z_L} - {Z_C})}^2}} }}.\sqrt {{R^2} + {Z_L}^2} } \end{array}\)

- Để điện áp hiệu dụng giữa hai đầu đoạn mạch AN không phụ thuộc R thì

\(\begin{array}{l} \sqrt {{R^2} + {{({Z_L} - {Z_C})}^2}} = \sqrt {{R^2} + {Z_L}^2} \\ \begin{array}{*{20}{l}} { \Rightarrow {Z_C} = 2{Z_L}}\\ { \Leftrightarrow \frac{1}{{C\omega }} = 2.L\omega \Rightarrow \omega = \frac{1}{{\sqrt {2LC} }}} \end{array} \end{array}\)

- Chọn D

Nối hai cực của một máy phát điện xoay chiều một pha vào hai đầu đoạn mạch AB gồm điện trở thuần R mắc nối tiếp với cuộn cảm thuần. Bỏ qua điện trở các cuộn dây của máy phát. Khi rôto của máy quay đều với tốc độ n vòng/phút thì cường độ dòng điện hiệu dụng trong đoạn mạch là 1A. Khi rôto của máy quay đều với tốc độ 3n vòng/phút thì cường độ dòng điện hiệu dụng trong đoạn mạch là √3A. Nếu rôto của máy quay đều với tốc độ 2n vòng/phút thì cảm kháng của đoạn mạch AB là

A. R/√3.                                   B. R/√3.

C. 2R/√3.                                 D. 2R/√3.

Phương pháp giải

- Công thức liên hệ giữa tốc độ góc và tốc độ quay của roto: 

ω= 2πf = 2πp.n

- Áp dụng công thức tính điện áp máy phát điện:

U= E= NBSω= NBS.2π.p.n

- Áp dụng định luật ôm để tính cường độ I

I = U/Z

Hướng dẫn giải

- Ta có:

+ ω= 2πf =2πpn ⇒ ω∼n

+U= E= NBSω= NBS.2πpn ⇒ U∼n

- Khi rôto của máy quay đều với tốc độ n vòng/phút, gọi điện áp máy phát điện xoay chiều khi đó là U, điện trở, cảm kháng lần lượt là R; Z_L

\(\Rightarrow I = \frac{U}{{\sqrt {{R^2} + {Z_L}^2} }} = 1(1)\)

- Khi rôto của máy quay đều với tốc độ 3n vòng/phút

 \(\begin{array}{*{20}{l}} \begin{array}{l} + {Z_{{L_2}}} = L{\omega _2} \Rightarrow {Z_{{L_2}}} \sim {\omega _2} \end{array}\\ { \Rightarrow {Z_{{L_2}}} \sim n}\\ { \Rightarrow {Z_{{L_2}}} = 3{Z_L}} \end{array}\)

+ U₂= 3U

\( \Rightarrow I = \frac{{3U}}{{\sqrt {{R^2} + 3{Z_L}^2} }} = \sqrt 3 (2)\)

- Từ (1)(2) ta có:

\(\frac{{3\sqrt {{R^2} + {Z_L}^2} }}{{\sqrt {{R^2} + 3{Z_L}^2} }} = \sqrt 3 \Rightarrow {Z_L} = \frac{R}{{\sqrt 3 }}\)

- Khi rôto của máy quay đều với tốc độ 3n vòng/phút 

\(\Rightarrow {Z_{{L_3}}} = 2{Z_L} = \frac{2}{{\sqrt 3 }}R\)

- Chọn C

Đặt điện áp u=U₀√2cosωt (U₀ và ω không đổi) vào hai đầu đoạn mạch AB theo thứ tự gồm một tụ điện, một cuộn cảm thuần và một điện trở thuần mắc nối tiếp. Gọi M là điểm nối giữa tụ điện và cuộn cảm. Biết điện áp hiệu dụng giữa hai đầu AM bằng điện áp hiệu dụng giữa hai đầu MB và cường độ dòng điện trong đoạn mạch lệch pha π/12 so với điện áp giữa hai đầu đoạn mạch AB. Hệ số công suất của đoạn mạch MB là

A. 0,5.                              B. √3/2.

C. √2/2.                            D. 0,26.

Phương pháp giải

- Vận dụng công thức tính hệ số công suất:

cosφ = U/R

- Hiệu điện thế được tính là:

\(U_C^2 = U_R^2 + U_L^2\)

- Chia hai vế cho U_C 

- Để tinh hệ số công suất ta tính:

 \(\begin{array}{*{20}{l}} {\tan \varphi = \frac{{{U_L} - {U_C}}}{{{U_R}}}}\\ \end{array}\)

- Áp dụng cho từng đoạn MB, AB

- Từ các phương trình mỗi đoạn mạch

⇒ cosφ = 0,5

Hướng dẫn giải

- Theo đề bài:

\({U_{AM}} = {U_{MB}} \Leftrightarrow {U_C} = {U_{RL}}(1)\)

⇒  Hệ số công suất đoạn MB:

\(\cos \varphi = \frac{{{U_R}}}{{{U_{RL}}}} = \frac{{{U_R}}}{{{U_C}}}\)

- Từ (1) ta có:

\(U_C^2 = U_R^2 + U_L^2\)

- Chia hai vế cho U_C được

\(\begin{array}{*{20}{l}} {1 = {{\left( {\frac{{{U_R}}}{{{U_C}}}} \right)}^2} + {{\left( {\frac{{{U_L}}}{{{U_C}}}} \right)}^2}}\\ { \Leftrightarrow 1 = {{\cos }^2}\varphi + {{\left( {\frac{{{U_L}}}{{{U_C}}}} \right)}^2}(2)} \end{array}\)

- Cường độ dòng điện trong đoạn mạch lệch pha π/12 so với điện áp giữa hai đầu đoạn mạch AB.

\(\begin{array}{l} \Rightarrow {\varphi _{AB}} = - \frac{\pi }{{12}}rad\\ {U_C} = {U_{RL}} > {U_L} \end{array}\)

- Ta có

\(\begin{array}{*{20}{l}} {\tan \varphi = \frac{{{U_L} - {U_C}}}{{{U_R}}}}\\ { \Leftrightarrow \tan ( - \frac{\pi }{{12}}) = \frac{{{U_L} - {U_C}}}{{{U_R}}}}\\ { \Leftrightarrow (\sqrt 3 - 2){U_R} = {U_L} - {U_C}} \end{array}\)

- Chia hai vế cho U_C được

\(\begin{array}{*{20}{l}} {(\sqrt 3 - 2)\frac{{{U_R}}}{{{U_C}}} = \frac{{{U_L}}}{{{U_C}}} - 1}\\ { \Leftrightarrow (\sqrt 3 - 2)\cos \varphi = \frac{{{U_L}}}{{{U_C}}} - 1}\\ { \Rightarrow \frac{{{U_L}}}{{{U_C}}} = (\sqrt 3 - 2)\cos \varphi + 1(4)} \end{array}\)

- Thay (4) vào (2) được:

\(\begin{array}{l} 1 = {\cos ^2}\varphi + {\left[ {(\sqrt 3 - 2)\cos \varphi + 1} \right]^2}\\ \Rightarrow \cos \varphi = 0,5 \end{array}\)

- Chọn A

Một máy biến áp có điện trở các cuộn dây không đáng kể. Điện áp hiệu dụng giữa hai đầu cuộn thứ cấp và giữa hai đầu cuộn sơ cấp lần lượt là 55V và 220V. Bỏ qua các hao phí trong máy. Tỉ số giữa số vòng dây của cuộn sơ cấp và số vòng dây của cuộn thứ cấp bằng

A. 8.                                  B. 4.

C. 2.                                   D. 14.

Phương pháp giải

Sử dụng lí thuyết máy biến áp lí tưởng:

\(\frac{{{U_1}}}{{{U_2}}} = \frac{{{N_1}}}{{{N_2}}}.\)

Hướng dẫn giải

- Ta có :

\(\frac{{{U_1}}}{{{U_2}}} = \frac{{{N_1}}}{{{N_2}}} \Rightarrow \frac{{{N_1}}}{{{N_2}}} = \frac{{220}}{{55}} = 4\)

- Chọn B

Máy biến áp là thiết bị

A. biến đổi tần số của dòng điện xoay chiều.

B. biến đổi dòng điện xoay chiều thành dòng điện một chiều.

C. có khả năng biến đổi điện áp của dòng điện xoay chiều.

D. làm tăng công suất của dòng điện xoay chiều.

Phương pháp giải

Máy biến áp có khả năng biến đổi điện áp của dòng điện xoay chiều

Hướng dẫn giải

- Máy biến áp là thiết bị có khả năng biến đổi điện áp của dòng điện xoay chiều.

- Chọn C

Một máy phát điện xoay chiều một pha có phần cảm là rôto gồm 4 cặp cực (4 cực nam và 4 cực bắc). Để suất điện động do máy này sinh ra có tần số 50Hz thì rôto phải quay với tốc độ

A. 750 vòng/phút.         

B. 75 vòng/phút.

C. 480 vòng/phút.         

D. 25 vòng/phút. 

Phương pháp giải

Sử dụng công thức tính tần số máy điện xoay chiều: f= pn

Hướng dẫn giải

- Có f= pn

⇒ n= f/p= 50/4= 12,5 (vòng/s)= 750 (vòng/phut)

- Chọn A

Trong mạch điện ba pha có tải đối xứng, khi dòng điện chạy trong tải thứ nhất có biểu thức là i₁=I√2cosωt, thì dòng điện chạy trong tải thứ hai và thứ ba có các biểu thức là:

A. i₂=I√2cos(ωt+π/3)(A) và i₃=I√2cos(ωt+2π/3)(A).

B. i₂=I√2cos(ωt+2π/3)(A) và i₃=I√2cos(ωt+π)(A).

C. i₂=I√2cos(ωt−π/3)(A) và i₃=I√2cos(ωt+π/3)(A).

D. i₂=I√2cos(ωt−2π/3)(A) và i₃=I√2cos(ωt+2π/3)(A).

Phương pháp giải

Vận dụng lí thuyết về động cơ điện ba pha.

Hướng dẫn giải

- Trong động cơ điện ba pha, dòng điện đôi một lệch pha nhau góc 2π/3 rad

i₂= I√2cos(ωt−2π/3)(A) và i₃= I√2cos(ωt+2π/3)(A).

- Chọn D

Đặt điện áp xoay chiều có giá trị hiệu dụng không đổi, tần số 50Hz vào hai đầu một đoạn mạch mắc nối tiếp gồm điện trở thuần R, cuộn cảm thuần có độ tự cảm L và tụ điện có điện dung C thay đổi được. Điều chỉnh điện dung C đến giá trị 10⁻⁴π(F)và 10⁻⁴/2π thì công suất tiêu thụ trên đoạn mạch đều có giá trị bằng nhau. Giá trị của L bằng bao nhiêu?

Phương pháp giải

- Tính tần số theo công thức: ω= 2πf

- Tính dung kháng theo công thức: Z_C = 1/Cω

- Tính cuộn cảm từ biểu thức công suất tiêu thụ bằng nhau

với P= I²R

- Suy ra cuộn cảm L

Hướng dẫn giải

- Tần số góc:

ω= 2πf= 100π (rad/s)

- Dung kháng là:

\(\begin{array}{l} {Z_{{C_1}}} = \frac{1}{{{C_1}\omega }} = \frac{1}{{\frac{{{{10}^{ - 4}}}}{{4\pi }}.100\pi }} = 400({\rm{\Omega }})\\ {Z_{{C_2}}} = \frac{1}{{{C_2}\omega }} = \frac{1}{{\frac{{{{10}^{ - 4}}}}{{2\pi }}.100\pi }} = 200({\rm{\Omega }}) \end{array}\)

- Công suất trên đoạn mạch hai trường hợp bằng nhau:

\(\begin{array}{*{20}{l}} {{P_1} = {P_2}}\\ { \Leftrightarrow I_1^2R = I_2^2R}\\ { \Leftrightarrow {I_1} = {I_2}}\\ { \Leftrightarrow {Z_1} = {Z_2}} \end{array}\)

- Cảm kháng là:

\(\begin{array}{*{20}{l}} {\sqrt {{R^2} + {{({Z_L} - {Z_{{C_1}}})}^2}} = \sqrt {{R^2} + {{({Z_L} - {Z_{{C_2}}})}^2}} }\\ { \Rightarrow 2{Z_L} = {Z_{{C_1}}} + {Z_{{C_2}}}}\\ { \Leftrightarrow {Z_L} = \frac{{{Z_{{C_1}}} + {Z_{{C_2}}}}}{2} = \frac{{400 + 200}}{2} = 300{\rm{\Omega }}} \end{array}\)

- Cuộn cảm là: 

\(\ L = \frac{{{Z_L}}}{\omega } = \frac{{300}}{{100\pi }} = \frac{3}{\pi }H\)

Một đoạn mạch gồm điện trở R=150Ω, cuộn cảm thuần có L=0,315H và tụ điện có C=16μF, mắc nối tiếp. Đặt điện áp xoay chiều có tần số f=50Hz và có điện áp hiệu dụng U=220V vào hai đầu đoạn mạch này. Hỏi:

a) Công suất tiêu thụ của đoạn mạch là bao nhiêu?

b) Phải thay tụ điện C bằng một tụ điện khác có điện dung C' bằng bao nhiêu để công suất tiêu thụ điện của mạch là lớn nhất?

Phương pháp giải

a) Tính tần số góc, cảm kháng và dung kháng

- Tính tổng trở theo công th: 

\(\begin{array}{l} Z = \sqrt {{R^2} + {{({Z_L} - {Z_C})}^2}} \\ \end{array}\)

- Tính công suất: P = I²R

b) Để công suất đạt cực đại mạch xảy ra hiện tưởng cộng hưởng

Hướng dẫn giải

- Tần số góc ω= 2πf= 100π (rad/s)

- Dung kháng:

\({Z_C} = \frac{1}{{C\omega }} = \frac{1}{{{{16.10}^{ - 6}}.100\pi }} \approx 200({\rm{\Omega }})\)

- Cảm kháng Z_L= Lω= 0,315.100π≈ 100(Ω)

- Tổng trở:

\(\begin{array}{l} Z = \sqrt {{R^2} + {{({Z_L} - {Z_C})}^2}} \\ = \sqrt {{{150}^2} + {{(100 - 200)}^2}} \approx 180{\rm{\Omega }} \end{array}\)

- Công suất:

\(P = {I^2}R = \frac{{{U^2}}}{{{Z^2}}}.R = \frac{{{{220}^2}.150}}{{{{180}^2}}} = 224W\)

b) Để công suất đạt cực đại mạch xảy ra hiện tưởng cộng hưởng khi đó

\(\begin{array}{*{20}{l}} {{Z_{C'}} = {Z_L} = 100{\rm{\Omega }}}\\ { \Rightarrow C' = \frac{1}{{{Z_{C'}}\omega }} = \frac{1}{{100.100\pi }} = \frac{{{{10}^{ - 4}}}}{\pi }F} \end{array}\)

Đặt điện áp xoay chiều vào hai đầu đoạn mạch RLC nối tiếp. Biết R=10Ω, cuộn cảm thuần có L=1/10π(H), tụ điện có C=10⁻³/2π(F)và điện áp giữa hai đầu cuộn cảm thuần là u_L=20√2cos(100πt+π/2)(V). Tìm biểu thức điện áp giữa hai đầu đoạn mạch.

Phương pháp giải

- Tính dung kháng Z_C= 1/Cω,  cảm kháng Z_L= Lω

- Tính tổng trở:

\({Z = \sqrt {{R^2} + {{({Z_L} - {Z_C})}^2}} }\)

- Biểu thức tính độ lệch pha giữa điện áp và dòng điện:

\(\varphi = {\varphi _u} - {\varphi _i};\,\,\tan \varphi = \frac{{{U_L} - {U_C}}}{{{U_R}}}\)

Hướng dẫn giải

- Dung kháng:

\({Z_C} = \frac{1}{{C\omega }} = \frac{1}{{\frac{{{{10}^{ - 3}}}}{{2\pi }}.100\pi }} = 20({\rm{\Omega }})\)

- Cảm kháng: Z_L= Lω= 1/10π.100π= 10(Ω)

- Tổng trở:

\(\begin{array}{l} Z = \sqrt {{R^2} + {{({Z_L} - {Z_C})}^2}} \\ = \sqrt {{{10}^2} + {{(10 - 20)}^2}} = 10\sqrt 2 {\rm{\Omega }} \end{array}\)

- Ta có u_L=20√2cos(100πt+π/2)(V).

⇒I₀= U_0L/Z_L=20√2/10=2√2A

- Độ lệch pha giữa điện áp hai đầu cuộn cảm và dòng điện 

Δφ= π/2= φ_uL−φ_i ⇒ φ_i= 0

- Điện áp cực đại hai đầu đoạn mạch:

U₀= I₀.Z= 2√2./10√2= 40V

- Độ lệch pha giữa điện áp hai đầu đoạn mạch và dòng điện φ\(\begin{array}{l} \begin{array}{*{20}{l}} {\tan \varphi = \frac{{{Z_L} - {Z_C}}}{R}}\\ { = \frac{{10 - 20}}{{10\sqrt 2 }} = - \frac{1}{{\sqrt 2 }}}\\ { \Rightarrow \varphi = - \frac{\pi }{4}rad} \end{array}\\ \varphi = {\varphi _u} - {\varphi _i} \Rightarrow {\varphi _u} = \varphi + {\varphi _i} = - \frac{\pi }{4}rad \end{array}\)

u_L=40cos(100πt−π/4)(V).

Đặt một điện áp u_L=150√2cos100πt vào hai đầu đoạn mạch mắc nối tiếp gồm điện trở thuần 60Ω, cuộn dây (có điện trở thuần) và tụ điện. Công suất tiêu thụ điện của đoạn mạch bằng 250W. Nối hai bản tụ điện bằng một dây dẫn có điện trở không đáng kể. Khi đó, điện áp hiệu dụng giữa hai đầu điện trở bằng điện áp hiệu dụng giữa hai đầu cuộn dây và bằng 50√3V. Hỏi dung kháng của tụ điện có giá trị bằng bao nhiêu?

Phương pháp giải

- Sử dụng định luật Ôm I=U/Z

- Sử dụng công thức tính công suất:

 P=I²(R+r)

Hướng dẫn giải

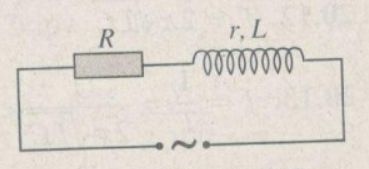
- Khi nối tắt tụ điện, mạch còn điện trở R và cuộn dây

\(\begin{array}{l} {U_R} = {U_{Lr}} \Leftrightarrow R = 60 = \sqrt {Z_L^2 + {r^2}} (1)\\ \begin{array}{*{20}{l}} {{U_R} = IR = \frac{{{\rm{UR}}}}{{\sqrt {{{(R + r)}^2} + Z_L^2} }}}\\ { \Leftrightarrow 50\sqrt 3 = \frac{{150.60}}{{\sqrt {{{(60 + r)}^2} + Z_L^2} }}(2)} \end{array} \end{array}\)

Từ (1)(2) giải được r=30Ω; Z_L=30√3Ω

- Khi tụ không bị nối tắt:

\(\begin{array}{*{20}{l}} {P = {I^2}(R + r) = \frac{{{U^2}(R + r)}}{{{{(R + r)}^2} + {{({Z_L} - {Z_C})}^2}}}}\\ { \Rightarrow 250 = \frac{{{{150}^2}(60 + 30)}}{{{{(60 + 30)}^2} + {{(30\sqrt 3 - {Z_C})}^2}}}}\\ { \Rightarrow {Z_C} = 30\sqrt 3 {\rm{\Omega }}} \end{array}\)