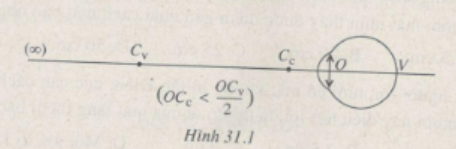Giải bài tập SBT Vật Lí 11 Bài 31: Mắt

Trong quá trình điều tiết của mắt thì

A. khoảng cách từ mắt đến điểm cực cận sẽ thay đổi.

B. khoảng cách từ mắt đến điểm cực viễn sẽ thay đổi.

C. khoảng cách từ thể thủy tinh đến võng mạc sẽ thay đổi.

D. độ tụ của mắt sẽ thay đổi. 

Phương pháp giải

Để trả lời câu hỏi nắm được đặc điểm hoạt động của mắt

Hướng dẫn giải

- Trong quá trình điều tiết của mắt thì độ tụ của mắt sẽ thay đổi. 

- Đáp án D

Gọi OV là khoảng cách từ thể thủy tinh đến võng mạc; f_max và f_min là các giá trị lớn nhất và nhỏ nhất của tiêu cực của mắt. Đối với mắt tốt (không có tật) thì

A. f_max > OV       B. f_max = OV

C. f_max < OV       D. f_min = OV 

Phương pháp giải

Mắt bình thường có tiêu cự cực bằng khoảng cách OV

Hướng dẫn giải

- Đối với mắt tốt (không có tật) thì  f_max = OV

- Chọn B

Khi mắt không điều tiết thì ảnh của điểm cực cận C_c được tạo ra ở đâu ?

A. Tại điểm vàng V.

B. Trước điểm vàng V.

C. Sau điểm vàng V.

D. Không xác định được vì không có ảnh. 

Phương pháp giải

Mắt bình thường khi không điều tiết thì ảnh của điểm cực cận C_c nằm sau điểm vàng

Hướng dẫn giải

- Khi mắt không điều tiết thì ảnh của điểm cực cận C_c được tạo ra ở sau điểm vàng V. 

- Đáp án C

Khi mắt điều tiết tối đa thì ảnh của điểm cực viễn C_v được tạo ra tại đâu ?

A. Tại điểm vàng V.

B. Trước điểm vàng V.

C. Sau điểm vàng V.

D. Không xác định được vì không có ảnh. 

Phương pháp giải

Mắt bình thường khi điều tiết tối đa thì ảnh của điểm cực viễn C_v nằm trước điểm vàng

Hướng dẫn giải

- Khi mắt điều tiết tối đa thì ảnh của điểm cực viễn C_v được tạo ra tại trước điểm vàng V. 

- Đáp án B

Đặt độ tụ của các loại mắt như sau ở trạng thái không điều tiết :

D₁ : Mắt bình thường (không tật) ; D₂ : Mắt cận ; D₃ : Mắt viễn

Coi khoảng cách từ thể thuỷ tinh đến võng mạc là như nhau. So sánh các độ tụ này ta có kết quả nào ?

A. D₁ > D₂ > D₃.      B. D₂ > D₁ > D₃.

C. D₃ > D₁ > D₂.      D. Một kết quả khác A, B, C. 

Phương pháp giải

Ở trạng thái không điều tiết, độ tụ của mắt giảm dần theo thứ từ: mắt cận, mắt bình thường và mắt viễn

Hướng dẫn giải

- Đặt độ tụ của các loại mắt ở trạng thái không điều tiết: D₂ > D₁ > D₃.

- Chọn B

Xét một mắt cận được mô tả ở Hình 31.1. Dùng các giả thiết đã cho để chọn đáp án đúng ở các câu hỏi từ 31.6 đến 31.9.

Vật có vị trí nào kể sau thì ảnh tạo bởi mắt hiện ra ở điểm vàng V ?

A. Tại C_v khi mắt điều tiết tối đa.

B. Tại C_c khi mắt không điều tiết.

C. Tại một điểm trong khoảng C_vC_c khi mắt điều tiết thích hợp.

D. Một vị trí khác với A, B, C. 

Phương pháp giải

Mắt bình thường khi không điều tiết nhìn vật ở C_c thì ảnh tạo ra ở điểm vàng V 

Hướng dẫn giải

-  Tại C_c khi mắt không điều tiết thì ảnh tạo bởi mắt hiện ra ở điểm vàng V 

- Chọn C

Để có thể nhìn rõ các vật ở vô cực mà không điều tiết, thì kính phải đeo sát mắt là kính phân kì có độ lớn của tiêu cự là :

A. |f| = O_CV.                   B. |f| = OC_c.

C. |f| = C_vC_c.                  D. |f| = OV 

Phương pháp giải

Để khắc phục tật cận thị của mắt cần đeo kính phân kì có tiêu cự là |f| = O_CV

Hướng dẫn giải

- Để có thể nhìn rõ các vật ở vô cực mà không điều tiết, thì kính phải đeo sát mắt là kính phân kì có độ lớn của tiêu cự là |f| = O_CV.       

- Đáp án A

Khi đeo kính để đạt yêu cầu như ở câu 31.7 thì điểm gần nhất mà mắt nhìn thấy là điểm nào ?

A. Vẫn là điểm C_c.

B. Một điểm ở trong đoạn OC_c.

C. Một điểm ở trong đoạn C_cC_v.

D. Một điểm ở ngoài đoạn O_CV. 

Phương pháp giải

Vận dụng lí thuyết về các tật của mắt để trả lời câu hỏi này

Hướng dẫn giải

- Khi đeo kính để đạt yêu cầu thì điểm gần nhất mà mắt nhìn thấy là một điểm ở trong đoạn OC_c

- Chọn B

Người này mua nhầm kính nên khi đeo kính sát mắt thì hoàn toàn không nhìn thấy gì. Có thể kết luận thế nào về kính này ?

A. Kính hội tụ có f >  OC_v.

B. Kính hội tụ có f < OC_C

C. Kính phân kì có |f| > OC_v.

D. Kính phân kì có |f| < OC_c. 

Phương pháp giải

Để trả lời câu hỏi này cần nắm được về cách khắc phục tật cận thị ở mắt

Hướng dẫn giải

- Khi đeo kính phân kì có |f| < OC_c sát mắt thì hoàn toàn không nhìn thấy gì

- Chọn D

Một người mắt cận đeo sát mắt kính -2 dp thì nhìn thấy rõ vật ở vô cực mà không điều tiết. Điểm C_c khi không đeo kính cách mắt 10 cm. Khi đeo kính, mắt nhìn thấy được điểm gần nhất cách mắt bao nhiêu ?

A. 12,5 cm.          B. 20 cm.

C. 25 cm.            D. 50 cm. 

Phương pháp giải

Áp dụng công thức: 

\(\frac{1}{{O{C_v}}} - \frac{1}{{O{C_c}}} = \frac{1}{f} = D\) để tìm khoảng đặt mắt gần vật nhất

Hướng dẫn giải

- Ta có:

\(f = O{C_v} = \frac{1}{D} = \frac{1}{2} = 50cm\)

D của mắt khi không đeo kính là: D=1/10

- Ta có: 

\(\frac{1}{{O{C_v}}} - \frac{1}{{O{C_c}}} = \frac{1}{f} = D\)

=> OC_c=12,5cm

- Khi đeo kính, mắt nhìn thấy được điểm gần nhất cách mắt 12,5 cm.   

- Đáp án A

Một người lớn tuổi có mắt không bị tật. Điểm cực cận cách mắt 50 cm. Khi người này điều tiết tối đa thì độ tụ của mắt tăng thêm bao nhiêu ?

A. 5 dp.        B. 2,5 dp.    

C. 2 dp.        D. Một giá trị khác A, B, C. 

Phương pháp giải

- Áp dụng công thức thấu kính để tính độ tụ cực đại và cực cận

- Tính khoảng tăng độ tụ theo công thức:

\({{D_{max}} - {D_{min}} = \Delta D}\)

Hướng dẫn giải

- Ta có:

\(\begin{array}{l} + \,\,\,\frac{1}{{O{C_v}}} + \frac{1}{{OV}} = \frac{1}{{{f_{max}}}} = {D_{min}}\\ + \,\,\,\frac{1}{{O{C_c}}} + \frac{1}{{OV}} = \frac{1}{{{f_{min}}}} = {D_{max}}\\ \Rightarrow {D_{max}} - {D_{min}} = {\rm{\Delta }}D\\ = \frac{1}{{O{C_c}}} - \frac{1}{{O{C_v}}} = \frac{1}{{0,5}} = 2dp \end{array}\)

Vậy khi người này điều tiết tối đa thì độ tụ của mắt tăng thêm 2 dp. 

- Đáp án C

Mắt của một người có tiêu cự của thể thuỷ tinh là 18 mm khi không điều tiết.

a) Khoảng cách từ quang tâm mắt đến võng mạc là 15 mm. Mắt bị tật gì ?

b) Xác định tiêu cự và độ tụ của thấu kính phải mang để mắt thấy vật ở vô cực không điều tiết (kính ghép sát mắt). 

Phương pháp giải

Áp dụng công thức:

\({\frac{1}{{{k_k}}} = \frac{1}{{OV}} - \frac{1}{{f_{{\rm{max}}}^{}}}}\) và \({{D_k} = \frac{1}{{{f_k}}}}\) để tìm tiêu cự và độ tụ của thấu kính

Hướng dẫn giải

a) Vì f_max > OV nên mắt viễn

b) Theo công thức về độ tụ:

\(\begin{array}{*{20}{l}} \begin{array}{l} \frac{1}{{{k_k}}} = \frac{1}{{OV}} - \frac{1}{{f_{{\rm{max}}}^{}}}\\ \Rightarrow {f_k} = \frac{{15.18}}{{18 - 15}} = 90mm = 9cm \end{array}\\ {{D_k} = \frac{1}{{{f_k}}} \approx 11dp} \end{array}\)

Mắt của một người có quang tâm cách võng mạc khoảng d’ = 1,52 cm. Tiêu cự thể thuỷ tinh thay đổi giữa hai giá trị f₁ = 1,500 cm và f₂ = 1,415 cm.

a) Xác định khoảng nhìn rõ của mắt.

b) Tính tiêu cự và độ tụ của thấu kính phải ghép sát vào mắt để mắt nhìn thấy vật ở vô cực không điều tiết.

c) Khi đeo kính, mắt nhìn thấy điểm gần nhất cách mắt bao nhiêu ? 

Phương pháp giải

a) Áp dụng công thức: C_VC_C=OC_v-OC_c để tìm khoảng nhìn rõ của mắt

Với OC_v và OC_c được tính từ công thức thấu kính

b) Tiêu cự và độ tụ đươc tính theo công thức:

f_k = - O_CV và D_k = 1/f_k

c) Tìm điểm gần nhất khi đeo kính theo công thức:

\(\begin{array}{l} \frac{1}{{ON}} = \frac{1}{{OC_c}} - \frac{1}{{OC_v}}\\\end{array}\)

Hướng dẫn giải

a) Xác định khoảng nhìn rõ của mắt

\(\begin{array}{*{20}{l}} \begin{array}{l} \frac{1}{{O{C_V}}} = \frac{1}{{{f_{{\rm{max}}}}}} - \frac{1}{{OV}} = \frac{1}{{1,5}} - \frac{1}{{1,52}}\\ \Rightarrow O{C_V} = \frac{{1,5.1,52}}{{1,52 - 1,5}} = 114cm \end{array}\\ \begin{array}{l} \frac{1}{{O{C_C}}} = \frac{1}{{{f_{\min }}}} - \frac{1}{{OV}} = \frac{1}{{1,415}} - \frac{1}{{1,52}}\\ \Rightarrow O{C_C} = \frac{{1,415.1,52}}{{1,52 - 1,415}} \approx 20,5cm \end{array} \end{array}\)$$

Khoảng nhìn rõ: C_VC_C = 114 – 20,5 = 93,5cm

b) f_k = - O_CV = -114cm 

⇒ D_k = 1/f_k = -1/1,14 ≈ -0,88dp

c) Điểm gần nhất N được xác định bởi:

\(\begin{array}{l} \frac{1}{{ON}} = \frac{1}{{20,5}} - \frac{1}{{114}}\\ \Rightarrow ON = \frac{{114.20,5}}{{114 - 20,5}} \approx 25cm \end{array}\)

Mắt của một người có điểm cực viễn và cực cận cách mắt lần lượt là 0,5 m và 0,15 m.

a) Người này bị tật gì về mắt ?

b) Phải ghép sát vào mắt thấu kính có độ tụ bao nhiêu để nhìn thấy vật đặt cách mắt 20 m không điều tiết ? 

Phương pháp giải

Áp dụng công thức: D=1/f để tính độ tụ của kính

Hướng dẫn giải

a) Vì C_V là thật (trước mắt); O_CV ≠ ∞ ⇒ Mắt cận.

b)  Tính độ tụ

\(\begin{array}{*{20}{l}} \begin{array}{l} \frac{1}{{{f_k}}} = \frac{1}{d} + \frac{1}{{d'}} = \frac{1}{{2000}} - \frac{1}{{50}}\\ \Rightarrow {f_k} = \frac{{50.2000}}{{ - 1950}} = - 51,3cm \end{array}\\ {{D_k} = \frac{1}{{{f_k}}} = - \frac{1}{{0,513}} \approx 1,95dp} \end{array}\)

Một người đứng tuổi nhìn rõ được các vật ở xa. Muốn nhìn rõ vật gần nhất cách mắt 27 cm thì phải đeo kính + 2,5 dp cách mắt 2 cm.

a) Xác định các điểm C_c và C_v của mắt.

b) Nếu đeo kính sát mắt thì có thể nhìn rõ các vật ở trong khoảng nào ? 

Phương pháp giải

a) Dựa vào công thức thấu kính để xác định điểm cực viễn và cực cận của mắt:

\({\frac{1}{{O'N}} - \frac{1}{{O'{C_C}}} = \frac{1}{{{f_k}}}}\) với f=1/D

b) Xác định các khoảng nhìn của mắt theo bảng bên dưới

Hướng dẫn giải

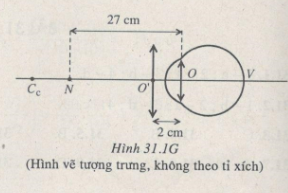
a) Ta có:

\(\begin{array}{l} {C_V} \to \infty \Rightarrow {f_k} = \frac{1}{{{D_k}}} = \frac{1}{{2,5}} = 0,4m = 40cm\\ \begin{array}{*{20}{l}} \begin{array}{l} \frac{1}{{O'N}} - \frac{1}{{O'{C_C}}} = \frac{1}{{{f_k}}}\\ \Rightarrow \frac{1}{{O'{C_C}}} = \frac{1}{{25}} - \frac{1}{{40}} \end{array}\\ { \Rightarrow O'{C_C} = \frac{{25.40}}{{40 - 25}} = \frac{{200}}{3}cm} \end{array} \end{array}\)

Vậy :

\(O{C_C} = \frac{{200}}{3} + 2 = \frac{{206}}{3} \approx 68,6cm\)

b) Tiêu cự của thấu kính tương đương với hệ (mắt + kính): 

\(\frac{1}{f} = \frac{1}{{{f_{mat}}}} + \frac{1}{{{f_k}}}\)

Khoảng phải tìm giới hạn bởi M và N xác định như sau:

Mắt của một người cận thị có điểm C_v cách mắt 20 cm.

a) Để khắc phục tật này, người đó phải đeo kính gì, độ tụ bao nhiêu để nhìn rõ các vật ở xa vô cùng ?

b) Người này muốn đọc một thông báo cách mắt 40 cm nhưng không có kính cận mà lại sử dụng một thấu kính phân kì có tiêu cự 15 cm. Để đọc được thông báo trên mà không phải điều tiết thì phải đặt thấu kính phân kì cách mắt bao nhiêu ? 

Phương pháp giải

a) Tính độ tụ của kính theo công thức: D­_k = 1/f_kvới  f_k = -OC_V 

b) Tìm vị trí đặt mắt theo công thức:

\({\frac{1}{{O'A}} - \frac{1}{{O'{C_V}}} = \frac{1}{{f_k^\prime }}}\)

Hướng dẫn giải

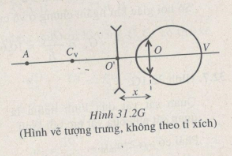
a) f_k = -OC_V = -20cm

D­_k = 1/f_k = -1/0,2 = -5 dp.

b) Ta có:

\(\begin{array}{l} \begin{array}{*{20}{c}} {\frac{1}{{O'A}} - \frac{1}{{O'{C_V}}} = \frac{1}{{f_k^\prime }}}\\ { \Rightarrow \frac{1}{{40 - x}} - \frac{1}{{20 - x}} = - \frac{1}{{15}}} \end{array}\\ \Rightarrow x{\rm{ }} = {\rm{ }}10cm \end{array}\)