Toán 7 Chương 1 Bài 3: Các góc tạo bởi một đường thẳng cắt hai đường thẳng

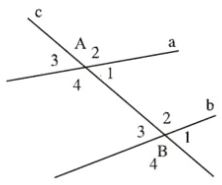
Trên hình vẽ, ta có:

- Hai cặp góc so le trong: $\widehat {{A_1}}$ và $\widehat {{B_3}}$; $\widehat {{A_2}}$ và  $\widehat {{B_4}}.$

- Bốn cặp góc đồng vị: $\widehat {{A_1}}$và $\widehat {{B_1}}$; $\widehat {{A_2}}$và $\widehat {{B_2}}$; $\widehat {{A_3}}$và $\widehat {{B_3}}$;$\widehat {{A_4}}$và $\widehat {{B_2}}$

Nếu đường thẳng c cắt hai đường thẳng a và b, trong các góc tạo thành có một cặp góc so le trong bằng nhau thì:

• Hai góc so le trong còn lại bằng nhau.
• Hai góc đồng vị (trong mỗi cặp) bằng nhau.

Câu 1: Vẽ đường thẳng a cắt hai đường thẳng b, c theo thứ tự B, C. Đánh số các góc đỉnh B, đỉnh C rồi viết tên hai cặp góc so le trong bốn cặp góc đồng vị.

Hướng dẫn giải

Hai cặp góc so le trong: $\widehat {{C_1}}$ và $\widehat {{B_3}};\,\widehat {{C_4}}$ và $\widehat {{B_2}}$

Bốn cặp góc đồng vị: $\widehat {{B_1}}$và $\widehat {{C_1}}$;$\widehat {{B_2}}$và $\widehat {{C_2}}$;$\widehat {{B_3}}$ và $\widehat {{C_3}};\,\,\,\widehat {{B_4}}$và $\,\widehat {{C_4}}$

Câu 2: Xét hai đường thẳng xy và BC trong hình, hãy cho biết:

a. Góc nào so le trong góc nào trong cùng phía đối góc c?

b. Góc nào so le trong góc nào trong cùng phía, góc nào đồng vị đối với góc A.

Hướng dẫn giải

a. $\widehat {{A_2}}$ so le trong với $\widehat C,\widehat {CAx}$ trong cùng phía với $\widehat {C.}$

b. $\widehat B$ so le trong với $\widehat {{A_1}},\widehat {{B_2}}$ trong cùng phía với $\widehat {{A_1}},\widehat {{B_3}}$ đồng vị với $\widehat {{A_1}}$

Câu 1:  Xét góc được ghi tên trong hình vẽ

a. Với hai đường thẳng AB và xy, hãy cho biết: Đối với đường thẳng AD thì cặp góc nào là cặp góc so le trong? Cũng hỏi như vậy đối với đường thẳng BC.

b. Với hai đường thẳng AD và BC, hãy cho biết: Đối với đường thẳng xy thì cặp góc nào là cặp góc đồng vị, cặp góc nào là cặp góc trong cùng phía, cặp góc nào là cặp góc ngoài cùng phía.

c. Cặp góc $\widehat {{B_1}}$ và $\widehat {{D_1}}$ là cặp góc so le trong đối với hai đường thẳng nào? Cũng hỏi như vậy đối với cặp góc $\widehat {{B_2}}$và $\widehat {{D_2}}$.

Câu 2: Cho hai đường thẳng a và b cắt đường thẳng thứ ba c. Nếu trong các góc tạo thành có một  cặp góc so le trong bằng nhau, các cặp góc còn lại phải thoả mãn điều kiện gì?

Câu 1: Chọn câu trả lời sai

Vẽ một đường thẳng cắt hai đường thẳng. Trong các góc tạo thành có một cặp góc so le trong bằng nhau. Khi đó:

A. Cặp góc so le trong còn lại bằng nhau  

B. Mỗi cặp góc đồng vị bằng nhau

C. Mỗi cặp góc trong cùng phía bù nhau

D. Mỗi cặp góc ngoài cùng phía bù nhau

Câu 2: Cho hình vẽ sau, chọn câu trả lời sai

A. $\widehat {{A_1}}$ và $\widehat {{B_1}}$ là hai góc đồng vị

B. $\widehat {{A_3}}$  và  $\widehat {{B_1}}$ là hai góc so le trong

C. $\widehat {{A_2}}$ và $\widehat {{A_4}}$  là hai góc đối đỉnh

D. $\widehat {{A_2}}$ và $\widehat {{B_1}}$ là hai góc so le trong

Câu 3: Cho đường thẳng a cắt hai đường thẳng b, c tại A, B như hình vẽ. Số cặp góc so le trong là:

A. 1

B. 2

C. 3

D. 4

Câu 4: Cho bốn điểm A, B, C, D. Hai đường thẳng AC, BD cắt nhau tại I như hình vẽ. Phát biểu nào sau đây là sai?

A. $\widehat {BAC},\,\,\widehat {BIC}$  đồng vị 

B. $\widehat {CAD},\,\,\widehat {ACB}$  so le trong

C. $\widehat {ADB},\,\,\widehat {CBD}$  so le trong

D. $\widehat {BAC},\,\,\widehat {ABC}$ so le trong

4. Kết luận 

Qua bài học này, các em cần nắm được những nội dung sau:

• Khái niệm, tính chất góc so le trong, góc đồng vị.

• Áp dụng để làm được các bài tập liên quan.