Lý 12 Bài 2: Con lắc lò xo

Con lắc lò xo: gồm một vật nhỏ có khối lượng m gắn vào đầu một lò xo có độ cứng k và khối lượng không đáng kể.

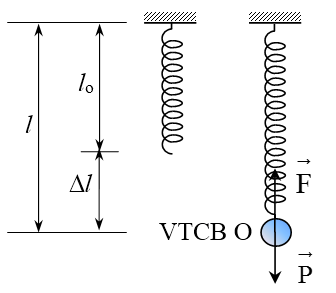
a. Xét vật ở li độ x, lò xo dãn một đoạn \(\Delta l = x\), lực đàn hồi \(F = - k\Delta l\)

Tổng lực tác dụng lên vật: \(F{\rm{ }} = - {\rm{ }}kx\)

Theo định luật II Niu tơn: \(a = - \frac{k}{m}x\)

Đặt: \({\omega ^2} = \frac{k}{m} \Rightarrow a + {\omega ^2}x = 0\)

b. Dao động của con lắc lò xo là dao động điều hòa

- Tần số góc: \({\omega ^2} = \frac{k}{m} \Rightarrow a + {\omega ^2}x = 0\)

- Chu kì: \(T = 2\pi \sqrt {\frac{m}{k}} \)

- Lực kéo về:

+ Biểu thức: \(T = 2\pi \sqrt {\frac{m}{k}} \)

+ Đặc điểm: 

• Là lực gây ra gia tốc cho vật dao động.

• Luôn hướng về vị trí cân bằng gọi là lực kéo về. Lực kéo về có độ lớn tỉ lệ với li độ và gây gia tốc cho vật dao động điều hòa.

• Biến thiên điều hoà cùng tần số với li độ.

a. Động năng của con lắc lò xo

\({W_d} = \frac{1}{2}m{v^2}(J)\)

b. Thế năng của con lắc lò xo

\({W_t} = \frac{1}{2}k{x^2}(J)\)

- Chú ý: Thế năng và động năng của con lắc lò xo biến thiên điều hòa với chu kì \(\frac{T}{2}.\)

c. Cơ năng của con lắc lò xo. Sự bảo toàn cơ năng

- Cơ năng của con lắc

\(W = \frac{1}{2}m{v^2} + \frac{1}{2}k{x^2}(J)\)

Khi không có ma sát thì cơ năng của con lắc được bảo toàn. Nó chỉ biến đổi từ thế năng sang động năng và ngược lại:

\( \Rightarrow W = \frac{1}{2}k{A^2} = \frac{1}{2}m{\omega ^2}{A^2} = \) hằng số

- Nhận xét

• Động năng và thế năng biến thiên cùng tần số góc \(2\omega ,\) tần số \(2f\), chu kỳ \(\frac{T}{2}\).

• Thời gian liên tiếp giữa 2 lần động năng bằng thế năng là \(\frac{T}{4}\).

• Cơ năng của con lắc lò xo luôn được bảo toàn và tỉ lệ với bình phương biên độ dao động.

Con lắc lò xo gồm vật có khối lượng m = 200 g và lò xo có độ cứng là k = 50 N/m. Tính chu kì dao động của con lắc lò xo. Lấy \({\pi ^2} = 10\).

Hướng dẫn giải

Chu kì dao động của con lắc lò xo:

\(T = 2\pi \sqrt {\frac{m}{k}} = 2\pi \sqrt {\frac{{0,2}}{{50}}} = 2\pi \sqrt {4.{\pi ^2}{{.10}^{ - 4}}} = 2\pi .2.\pi {.10^{ - 2}} = 0,4\) s

Con lắc lò xo treo thẳng đứng gồm một vật có khối lượng 100 g và lò xo có khối lượng không đáng kể, có độ cứng 40 N/m. Kéo vật nặng thẳng đứng xuống phía dưới cách vị trí cân bằng 5 cm và thả nhẹ cho vật dao động điều hòa. Chọn trục Ox thẳng đứng, gốc O trùng với vị trí cân bằng, chiều dương là chiều vật bắt đầu chuyển động, gốc thời gian là lúc thả vật. Lấy g = 10 m/s². Viết phương trình dao động của vật.

Hướng dẫn giải

Phương trình dao động của vật có dạng: \({\rm{x}} = Ac{\rm{os}}\left( {\omega t + \varphi } \right)\)

\(\omega = \sqrt {\frac{k}{m}} = \sqrt {\frac{{40}}{{0,1}}} = \sqrt {400} = 20\) rad/s

Chọn t = 0 lúc \(x = - A = - 5\) cm, khi đó:

 \(c{\rm{os}}\varphi = \frac{{ - x}}{A} = \frac{{ - 5}}{5} = - 1 \Rightarrow \varphi = \pi \)

Vậy phương trình dao động của vật là: \(x = 5c{\rm{os}}\left( {20t + \pi } \right)\) cm

Câu 1: Một con lắc lò xo dao động với chu kì là 0,5 s, khối lượng của quả nặng là m = 400 g. Lấy \({\pi ^2} = 10\). Tính độ cứng của lò xo?

Câu 2: Một con lắc lò xo dao động thẳng đứng. Vật có khối lượng m = 200 g. Trong 20 s con lắc thực hiện được 50 dao động toàn phần. Tính độ cứng của lò xo. Lấy \({\pi ^2} = 10\).

Câu 3: Một con lắc lò xo gồm vật nặng có khối lượng 400 g, lò xo có khối lượng không đáng kể, có độ cứng 40 N/m. Kéo vật nặng ra khỏi vị trí cân bằng 4 cm và thả nhẹ. Chọn chiều dương cùng chiều với chiều kéo vật, gốc thời gian là lúc thả vật. Viết phương trình dao động của vật.

Câu 4: Một con lắc lò xo gồm vật nặng có khối lượng 50 g dao động trên trục Ox với chu kì 0,2 s và chiều dài quỹ đạo là 40 cm. Viết phương trình dao động của con lắc. Chọn gốc thời gian là lúc con lắc qua vị trí cân bằng theo chiều âm.

Câu 1: Một con lắc lò xo nằm ngang lò xo nhẹ có độ cứng k = 100 N/m và vật nhỏ có khối lượng m = 100 g. Kích thích cho con lắc dao động, lấy \(\pi = \sqrt {10} \). Tần số của con lắc là:

A. 5 Hz                                             B. 6 Hz  

C. 10 Hz                                           D. 12 Hz

Câu 2: Một con lắc lò xo có vật nặng m = 200 g dao động  điều hòa. Trong 10 s thực hiện được 50 dao động. Lấy π² = 10. Độ cứng của lò xo này là:

A. 50 N/m                                          B. 100 N/m   

C. 150 N/m                                        D. 200 N/m

Câu 3: Một con lắc lò xo dao động điều hòa có thời gian giữa hai lần liên tiếp đi qua vị trí cân bằng là 0,2 s. Độ cứng lò xo là 100 N/m. Lấy π² = 10. Vật nặng có khối lượng là:

A. 100 g                                             B. 75 g  

C. 400 g                                             D. 200 g

Câu 4: Một con lắc lò xo treo thẳng đứng, vật nặng khối lượng m = 250 g. Chọn Ox thẳng đứng, chiều dương hướng xuống, gốc tọa độ tại vị trí cân bằng. Kéo vật xuống dưới đến vị trí lò xo giãn 6,5 cm rồi thả nhẹ, vật dao động điều hòa với năng lượng 80 mJ. Chọn t = 0 lúc thả vật, lấy g =10 m/s². Phương trình dao động của vật.

A. x = 6,5cos(5πt) cm                         B. x = 4cos(20t + π) cm  

C. x = 6,5cos(5πt + \(\frac{\pi }{2}\)) cm                  D. x = 4cos(20t) cm

Qua bài Con lắc lò xo này, các em cần hoàn thành 1 số mục tiêu mà bài đưa ra như:

• Công thức tính thế năng động năng và cơ năng của con lắc lò xo.
• Áp dụng được các công thức và định luật có trong bài để giải được các bài tập căn bản.
• Viết được phương trình động học của con lắc lò xo.