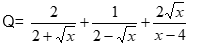10 đề thi giữa HK1 môn Toán 9 năm 2021 - 2022 có đáp án
Cùng tham gia thử sức với bộ 10 đề thi giữa HK1 Toán 9 năm 2021-2022 có đáp án để nâng cao tư duy, rèn luyện kĩ năng giải đề và củng cố kiến thức căn bản. Chúc các em vượt qua kì thi sắp tới thật dễ dàng nhé!
Mục lục nội dung

1. Đề cương ôn tập giữa HK1 môn Toán 9
ĐỀ CƯƠNG ÔN TẬP GIỮA HỌC KÌ 1
MÔN TOÁN 9
NĂM HỌC 2021-2022
I. Các kiến thức trọng tâm
1.1. Đại số
- Vận dụng các phép biến đổi đơn giản biểu thức chứa căn thức bậc hai để tính giá trị của biểu thức, rút gọn biểu thức, chứng minh đẳng thức; tìm giá của x để biểu thức nhận giá trị nguyên; tìm giá trị lớn nhất, giá trị nhỏ nhất của biểu thức; chứng minh bất đẳng thức, …
- Giải bài toán tìm x.
1.2. Hình học
Hệ thức lượng trong tam giác vuông.
- Vận dụng các hệ thức về cạnh và đường cao trong tam giác vuông để:- Tính các yếu tố về cạnh, đường cao, hình chiếu của các cạnh góc vuông trên cạnh huyền.
- Chứng minh các hệ thức, giải bài toán diện tích, cực trị hình học, …
- Vận dụng các tỉ số lượng giác của góc nhọn, hệ thức về cạnh và góc trong tam giác vuông giải tam giác vuông (tìm các yếu tố về cạnh và góc của tam giác vuông).
2. Bài tập
2.1. Bài tập tự luận
Câu 1: Cho biểu thức: P = \(\left( {\frac{{x\sqrt x - 1}}{{x - \sqrt x }} - \frac{{x\sqrt x + 1}}{{x + \sqrt x }}} \right):\left[ {\frac{{2(x - 2\sqrt x + 1)}}{{x - 1}}} \right]\)
Rút gọn P
Câu 2: Cho nửa đường tròn (O) đường kính AB. Vẽ các tiếp tuyến Ax, By về nửa mặt phẳng bờ AB chứa nửa đường tròn. Trên Ax và By theo thứ tự lấy M và N sao cho góc MON bằng 900
Gọi I là trung điểm của MN. Chứng minh rằng:
a) AB là tiếp tuyến của đường tròn (I;IO)
b) MO là tia phân giác của góc AMN
c) MN là tiếp tuyến của đường tròn đường kính AB
Hướng dẫn giải
Câu 1:
a)
- ĐKXĐ: \(0 \le x \ne 1\)
- Rút gọn
P = \(\left( {\frac{{{{\sqrt x }^3} - {1^3}}}{{\sqrt x (\sqrt[{}]{x} - 1\left. {} \right)}} - \frac{{{{\sqrt x }^3} + {1^3}}}{{\sqrt x (\sqrt x + 1)}}} \right):\left( {\frac{{2.{{(\sqrt x - 1)}^2}}}{{{{\sqrt x }^2} - {1^2}}}} \right)\)
\( \Leftrightarrow P = \left( {\frac{{(\sqrt x - 1)(x + \sqrt x + 1)}}{{\sqrt x (\sqrt x - 1)}} - \frac{{(\sqrt x + 1)(x - \sqrt x + 1)}}{{\sqrt x (\sqrt x + 1)}}} \right):\left( {\frac{{2{{(\sqrt x - 1)}^2}}}{{(\sqrt x - 1)(\sqrt x + 1)}}} \right)\)
\( \Leftrightarrow P = \left( {\frac{{x + \sqrt x + 1}}{{\sqrt x }} - \frac{{x - \sqrt x + 1}}{{\sqrt x }}} \right):\left( {\frac{{2(\sqrt x - 1)}}{{\sqrt x + 1}}} \right)\)
\(\Leftrightarrow P = \left( {\frac{{x + \sqrt x + 1 - x + \sqrt x - 1}}{{\sqrt x }}} \right).\left( {\frac{{\sqrt x + 1}}{{2(\sqrt x - 1)}}} \right)\)
\( \Leftrightarrow P = \left( {\frac{{2\sqrt x }}{{\sqrt x }}} \right).\left( {\frac{{\sqrt x + 1}}{{2(\sqrt x - 1)}}} \right)\)
\( \Leftrightarrow P = \frac{{\sqrt x + 1}}{{\sqrt x - 1}}\)
Câu 2:
a) Tứ giác ABNM có AM//BN (vì cùng vuông góc với AB) => Tứ giác ABNM là hình thang.
Hình thang ABNM có: OA= OB; IM=IN nên IO là đường trung bình của hình thang ABNM.
Do đó: IO//AM//BN.
Mặt khác: AM AB suy ra IO AB tại O.
Vậy AB là tiếp tuyến của đường tròn (I;IO)
b) Ta có: IO//AM => \(\widehat {AMO}\) = \(\widehat {MOI}\) (sole trong) ( 1)
Lại có: I là trung điểm của MN và rMON vuông tại O (gt)
nên MIO cân tại I.
Hay \(\widehat {OMN}\)= \(\widehat {MOI}\)(2)
Từ (1) và (2) suy ra: \(\widehat {AMO}\) = \(\widehat {OMN}\). Vây MO là tia phân giác của AMN.
c) Kẻ OH vuông góc MN (H thuộc MN). (3)
Xét tam giác OAM và tam giác OHM có:
\(\widehat {OAM}\) = \(\widehat {OHM}\) = 900
\(\widehat {AMO}\) = \(\widehat {OMN}\). ( chứng minh trên)
MO là cạnh chung
Suy ra: tam giác OAM = tam giác OHM (cạnh huyền- góc nhọn)
Do đó: OH = OA => OH là bán kính đường tròn (O; \(\frac{{AB}}{2}\)). (4)
Từ (3) và (4) suy ra: MN là tiếp tuyến của đường tròn (O; \(\frac{{AB}}{2}\))
2.2. Bài tập trắc nghiệm
Câu 1: Biểu thức \(\sqrt {2x - 1}\)xác định khi:
A. \(x \le \frac{1}{2}\)
B. \(x \ge \frac{1}{2}\)
C. \(x < \frac{1}{2}\)
D. \(x > \frac{1}{2}\)
Câu 2: Hàm số \(y = - 2x + 1\) có đồ thị là hình nào sau đây?
.png)
Câu 3: Giá trị của biểu thức \(\frac{1}{{2 + \sqrt 3 }} + \frac{1}{{2 - \sqrt 3 }}\) bằng
A. \(\frac{1}{2}\)
B. 1
C. 4
D. - 4
Câu 4: Đường tròn là hình:
A. Không có trục đối xứng
B. Có một trục đối xứng
C. Có hai trục đối xứng
D. Có vô số trục đối xứng
---(Để xem tiếp nội dung của đề thi các em vui lòng xem tại online hoặc đăng nhập để tải về máy)---
2. Đề thi
2.1. Đề thi giữa HK1 môn Toán 9 – Số 1
TRƯỜNG TRƯỜNG THCS ĐĂNG KHOA
ĐỀ THI GIỮA HK1
NĂM HỌC: 2021-2022
MÔN: TOÁN 9
Phần I. Trắc nghiệm
Câu 1: Căn bậc hai của 9 là:
A. 81
B. \(\pm\)81
C . 3
D . \(\pm\)3
Câu 2: Phương trình \(\sqrt {x - 2} = 3\) có nghiệm là:
A. 9
B. \(\pm\)9
C. \(\pm\)4
D. 11
Câu 3: Điều kiện xác định của \(\sqrt {4 + 2x} \) là:
A. x \(\ge\) 0
B. x \(\ge\) 2
C. x \(\ge \)-2
D. x \(\le \)2
Câu 4: Kết quả của phép khai phương \(\sqrt {81{{\rm{a}}^{\rm{2}}}} \) (với a < 0) là:
A. -9a
B. 9a
C. -9\(\left| {\rm{a}} \right|\)
D. 81a
Câu 5: Tìm x biết \(\sqrt[3]{x}\)= -5:
A. x = -25
B. x = -125
C. x = -512
D. x = 15
Câu 6: Rút gọn biểu thức \(\sqrt{{{\left( \sqrt{7}\,-\,4 \right)}^{2}}}\) ta được kết quả cuối cùng là:
A. \(\sqrt{7}\,+\,4\)
B. \(4\,-\,\sqrt{7}\)
C. \(\sqrt{7}\,-\,4\)
D. \(\sqrt{3}\)
Câu 7: Trong hệ tọa độ Oxy, đường thẳng y = 2 - x song song với đường thẳng:
A . y = -x
B . y = -x + 3
C . y = -1 - x
D . Cả ba đường thẳng trên
Câu 8. Trong các hàm số bậc nhất sau, hàm số nào là hàm số nghịch biến:
A. \(y=1-3x\)
B. \(y=5x-1\)
C. y = \(\left( 2-\sqrt{3} \right)x\,-\,\sqrt{5}\)
D. \(y=-\sqrt{7}+\sqrt{2}x\)
Câu 9. Nếu điểm B(1 ;-2) thuộc đường thẳng y = x – b thì b bằng:
A. -3
B. -1
C. 3
D. 1
Câu 10 : Cho hai đường thẳng: (d) : y = 2x + m – 2 và (d’) : y = kx + 4 – m; (d) và (d’) trùng nhau nếu :
A. k = 2 và m = 3
B. k = -1 và m = 3
C. k = -2 và m = 3
D. k = 2 và m = -3
Câu 11 :Góc tạo bởi đường thẳng y=x+1 và trục Ox có số đo là:
A. 450
B. 300
C. 600
D. 1350.
Câu 12 :Hệ số góc của đường thẳng: y=-4x+9 là:
A. 4
B. -4x
C. -4
D. 9
Phần II. Tự luận
Câu 1:Tính:
a) \(\sqrt{8}-2\sqrt{32}+3\sqrt{50}\)
b) \(\frac{1}{3+\sqrt{2}}-\frac{1}{3-\sqrt{2}}\)
Câu 2: Cho biểu thức:
a) Rút gọn biểu thức Q.
b) Tìm x để Q = 6/5
Câu 3: Cho hàm số y = (m + 1)x – 3. (m \(\ne \) -1). Xác định m để :
a) Hàm số đã cho đồng biến, nghịch biến trên R.
b) Đồ thị hàm số song song với đường thẳng y = 2x. Vẽ đồ thị với m vừa tìm được.
ĐÁP ÁN ĐỀ SỐ 1
Phần I. Trắc nghiệm
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
D |
D |
C |
A |
B |
B |
D |
A |
C |
A |
A |
C. |
..........
---(Để xem tiếp nội dung của đề thi các em vui lòng xem tại online hoặc đăng nhập để tải về máy)---
2.2. Đề thi giữa HK1 môn Toán 9 – Số 2
TRƯỜNG TRƯỜNG THCS HOÀNG DIỆU
ĐỀ THI GIỮA HK1
NĂM HỌC: 2021-2022
MÔN: TOÁN 9
Câu 1.
a)Tính giá trị của biểu thức A và B:
\(A = \sqrt {144} + \sqrt {36}\)
\(B = \sqrt {6,4} + \sqrt {250} \)
b) Rút gọn biểu thức : \(7\sqrt {12} + 2\sqrt {27} - 4\sqrt {75}\)
c) Chứng minh rằng giá trị của biểu thức sau không phụ thuộc vào giá trị của a:
\(M = \left( {\frac{{1009}}{{\sqrt a - 1}} + \frac{{1009}}{{\sqrt a + 1}}} \right) \cdot \left( {\sqrt a - \frac{1}{{\sqrt a }}} \right)\) với \(a > 0\) và \(a \ne {\rm{1}}\)
Câu 2. Cho hàm số y = ax -2 có đồ thị là đường thẳng
a) Biết đồ thị hàm số qua điểm A(1;0). Tìm hệ số a, hàm số đã cho là đồng biến hay nghịch biến trên R? Vì sao?
b) Vẽ đồ thị hàm số vừa tìm được.
c) Với giá trị nào của m để đường thẳng ${{d}_{2}}$: y=(m-1)x+3 song song ${{d}_{1}}$?
Câu 3. Cho tam giác ABC, đường cao AH, biết AB = 30cm, AC = 40cm,
BC = 50cm.
a) Chứng minh tam giác ABC vuông tại A
b) Tính đường cao AH?
c) Tính diện tích tam giác AHC?
ĐÁP ÁN ĐỀ SỐ 2
Câu 1:
\(A=\sqrt{144}+\sqrt{36}\)
\(=\sqrt{{{12}^{2}}}+\sqrt{{{6}^{2}}}\)
\(=12+6=18\)
\(\begin{gathered}
B = \sqrt {6,4} .\sqrt {250} \hfill \\
= \sqrt {6,4.250} \hfill \\
= \sqrt {64.25} \hfill \\
= 8.5 = 40 \hfill \\
\end{gathered} \)
b) \(7\sqrt{12}+2\sqrt{27}-4\sqrt{75}\)
\(=7\sqrt{4.3}+2\sqrt{9.3}-4\sqrt{25.3}\)
\( =7.2\sqrt{3}+2.3\sqrt{3}-4.5\sqrt{3}\)
\(=14\sqrt{3}+6\sqrt{3}-20\sqrt{3}\)
\(=(14+6-20)\sqrt{3}=0\)
..........
---(Để xem tiếp nội dung của đề thi các em vui lòng xem tại online hoặc đăng nhập để tải về máy)---
2.3. Đề thi giữa HK1 môn Toán 9 – Số 3
TRƯỜNG TRƯỜNG THCS NGỌC SƠN
ĐỀ THI GIỮA HK1
NĂM HỌC: 2021-2022
MÔN: TOÁN 9
Bài 1
Trục căn thức ở mẫu: \(\frac{4}{2\sqrt{3}+4}\)
Bài 2
a) Thực hiện phép tính: \(4\sqrt{75}-3\sqrt{108}-9\sqrt{\frac{1}{3}}\)
b) Tìm giá trị lớn nhất của biểu thức: \(y=3\sqrt{x}-x\)
Bài 3
a) Vẽ trên cùng một mặt phẳng tọa độ Oxy đồ thị của các hàm số sau: y = x + 2 và y = -2x + 5.
b) Gọi giao điểm của các đường thẳng y = x + 2 và y = -2x + 5 với trục hoành theo thứ tự là A và B; gọi giao điểm của hai đường thẳng trên là C. Tìm tọa độ của điểm C. Tính chu vi và diện tích của tam giác ABC(đơn vị đo trên các trục tọa độ là xentimét và làm tròn đến chử số thập phân thứ hai).
ĐÁP ÁN ĐỀ SỐ 3
Bài 1:
Trục căn thức ở mẫu: \(\frac{4}{2\sqrt{3}+4}\)
\(\begin{gathered}
\frac{4}{{2\sqrt 3 + 4}} = \frac{{4\left( {2\sqrt 3 - 4} \right)}}{{\left( {2\sqrt 3 + 4} \right)\left( {2\sqrt 3 - 4} \right)}} \hfill \\
{\mkern 1mu} = \frac{{4\left( {3\sqrt 2 - 4} \right)}}{{{{\left( {3\sqrt 2 } \right)}^2} - {4^2}}} \hfill \\
{\mkern 1mu} = 2\left( {3\sqrt 2 - 4} \right) \hfill \\
\end{gathered} \)
Bài 2:
a) Thực hiện phép tính: \(4\sqrt{75}-3\sqrt{108}-9\sqrt{\frac{1}{3}}\)
\(\begin{gathered}
= 4\sqrt {{5^2}.3} - 3\sqrt {{6^2}.3} - 9\sqrt {\frac{{1.3}}{{{3^2}}}} \hfill \\
= 4.5\sqrt 3 - 3.6\sqrt 3 - 3\sqrt 3 \hfill \\
= - \sqrt 3 \hfill \\
\end{gathered} \)
b) Tìm giá trị lớn nhất của biểu thức: \(y=3\sqrt{x}-x\)
Bài 3:
a) Vẽ trên cùng một mặt phẳng tọa độ Oxy đồ thị của các hàm số sau: y = x + 2 và y = -2x + 5.
Vẽ đồ thị hàm số y =x+2 .
Cho x = 0 y = 2 được (0 ;2)
Cho y = 0 x = -2 được (-2 ;0)
Vẽ đồ thị hàm số y = -2x+5 .
Cho x = 0 y = 5 được (0 ;5)
Cho y = 0 x = 2,5 được (2,5;0)
..........
---(Để xem tiếp nội dung của đề thi các em vui lòng xem tại online hoặc đăng nhập để tải về máy)---
2.4. Đề thi giữa HK1 môn Toán 9 – Số 4
TRƯỜNG TRƯỜNG THCS ĐIỆN BIÊN
ĐỀ THI GIỮA HK1
NĂM HỌC: 2021-2022
MÔN: TOÁN 9
Câu 1:
a) Phát biểu quy tắc chia hai căn bậc hai?
b) Tính: \(\frac{\sqrt{432}}{\sqrt{12}}\)
Câu 2: Thực hiện phép tính: \((\sqrt{12}+\sqrt{27}-\sqrt{108}).2\sqrt{3}\)
Câu 3: Cho biểu thức :
M = \(\frac{{{x}^{3}}}{{{x}^{2}}-4}-\frac{x}{x-2}-\frac{2}{x+2}\)
a) Tìm điều kiện để biểu thức M xác định.
b) Rút gọn biểu thức M.
Câu 4:
Cho các hàm số \(y=-x+2,\,\,\,y=x+4\). Lần lượt có đồ thị là các đường thẳng \({{d}_{1}}\]và \[{{d}_{2}}\).
a) Vẽ \({{d}_{1}}\) và \({{d}_{2}}\) trên cùng một hệ trục tọa độ Oxy.
b) Lập phương trình của đường thẳng \({{d}_{3}}\) biết rằng \({{d}_{3}}\) đi qua điểm M(2;-1) và song song với đường thẳng \({{d}_{1}}\).
Tìm điểm A thuộc đường thẳng \({{d}_{1}}\) có hoành độ và tung độ bằng nhau.
ĐÁP ÁN ĐỀ SỐ 4
Câu 1:
a) Phát biểu đúng quy tắc chia hai căn bậc hai.
b) \(\frac{\sqrt{432}}{\sqrt{12}}=\sqrt{\frac{432}{12}}=\sqrt{36}=6\)
Câu 2:
\(\begin{gathered}
(\sqrt {12} + \sqrt {27} - \sqrt {108} ).2\sqrt 3 \hfill \\
= (\sqrt {4.3} + \sqrt {9.3} - \sqrt {36.3} ).2\sqrt 3 \hfill \\
= (2\sqrt 3 + 3\sqrt 3 - 6\sqrt 3 ).2\sqrt 3 \hfill \\
= - \sqrt 3 .2\sqrt 3 = - 6 \hfill \\
\end{gathered} \)
Câu 3:
a) Điều kiện : x\(\ne 2\) ,x\(\ne -2\)
b) M = \(\frac{{{x}^{3}}}{{{x}^{2}}-4}-\frac{x}{x-2}-\frac{2}{x+2}\)
= \(\frac{{{x}^{3}}-x(x+2)-2(x-2)}{{{x}^{2}}-4}\)
\(=\frac{{{x}^{3}}-{{x}^{2}}-2x-2x+4}{{{x}^{2}}-4}=\frac{{{x}^{3}}-4x-{{x}^{2}}+4}{{{x}^{2}}-4}=\frac{x({{x}^{2}}-4)-({{x}^{2}}-4)}{{{x}^{2}}-4}\)
= \(\frac{({{x}^{2}}-4)(x-1)}{{{x}^{2}}-4}=x-1\)
-----Còn tiếp-----
2.5. Đề thi giữa HK1 môn Toán 9 – Số 5
TRƯỜNG TRƯỜNG THCS LÊ LỢI
ĐỀ THI GIỮA HK1
NĂM HỌC: 2021-2022
MÔN: TOÁN 9
Phần I.Trắc nghiệm
Câu 1.Căn bậc hai số học của 9 là
|
A. -3. |
B. 3. |
C. 81. |
D. -81. |
Câu 2.Biểu thức \(\sqrt {1 - 2x} \) xác định khi:
|
A. \(x > \frac{1}{2}\) |
B. \(x \ge \frac{1}{2}\) |
C. \(x < \frac{1}{2}\) |
D. \(x \le \frac{1}{2}\) |
Câu 3: Hàm số y =(2m+6)x + 5 là hàm số bậc nhất khi
A. x > -3 ; B. m \(\ne \) 3; C. m \(\ne \) - 3; D. x < 3.
Câu 4: Hàm số y =(-m+3)x -15 là hàm số đồng biến khi
A. m > -3 ; B. m \(\ne \) 3; C. m \(\ge \) 3; D. m < 3
Câu 5.Biểu thức \(\sqrt {{{\left( {3 - 2x} \right)}^2}}\) bằng
|
A. 3 – 2x. |
B. 2x – 3. |
C. \(\left| {2x - 3} \right|\) |
D. 3 – 2x và 2x – 3. |
Câu 6.Giá trị của biểu thức \(c{\rm{o}}{{\rm{s}}^{\rm{2}}}{20^0} + c{\rm{o}}{{\rm{s}}^{\rm{2}}}{40^0} + c{\rm{o}}{{\rm{s}}^{\rm{2}}}{50^0} + c{\rm{o}}{{\rm{s}}^{\rm{2}}}{70^0}\) bằng
|
A. 1. |
B. 2. |
C. 3. |
D. 0. |
Câu 7.Giá trị của biểu thức \(\frac{1}{{2 + \sqrt 3 }} + \frac{1}{{2 - \sqrt 3 }}\) bằng
|
A. \(\frac{1}{2}\) |
B. 1. |
C. -4. |
D. 4. |
Câu 8.Cho tam giác ABC vuông tại A có AB = 18; AC = 24. Bán kính đường tròn ngoại tiếp tam giác đó bằng
|
A. 30. |
B. 20. |
C. 15. |
D. 15 . |
Câu 9.Trong các hàm số sau, hàm số nào là hàm số bậc nhất ?
|
A. \(y = \sqrt {\frac{x}{2}} + 4\) |
B. \(y = \frac{{\sqrt 2 x}}{2} - 3\) |
C. \(y = \frac{{ - 2}}{x} + 1\) |
D. \(y = - \frac{{3\sqrt x }}{5} + 2\) |
Câu 10.Trong các hàm số sau, hàm số nào đồng biến ?
A. y = 2 – x B. \(y = - \frac{1}{2}x + 1\) C. \(y = \sqrt 3 - \sqrt 2 \left( {1 - x} \right)\) D. y = 6 – 3(x – 1).
-----Còn tiếp-----
2.6. Đề thi giữa HK1 môn Toán 9 – Số 6
TRƯỜNG TRƯỜNG THCS VÕ THỊ SÁU
ĐỀ THI GIỮA HK1
NĂM HỌC: 2021-2022
MÔN: TOÁN 9
Phần I. Trắc nghiệm
Câu 1: \(\sqrt {21 - 7x}\)có nghĩa khi
A. x \(\ge \)- 3;
B. x \(\le \) 3 ;
C. x > -3 ;
D. x <3.
Câu 2: Rút gọn biểu thức \(\sqrt {(5 - \sqrt {13} ){}^2} \) được
A. 5 - \(\sqrt {13}\)
B. -5 - \(\sqrt {13}\)
C. \(\sqrt {13}\)- 5
D. \(\sqrt {13}\) + 5.
Câu 3: Rút gọn các biểu thức \(3\sqrt {3a} + 4\sqrt {12a} - 5\sqrt {27a}\) (a \(\ge \) 0) được
A. \(4\sqrt {3a}\)
B. \(26\sqrt {3a}\)
C. \(-26\sqrt {3a}\)
D. \(-4\sqrt {3a}\)
Câu 4: Giá trị biểu thức \(\sqrt {16} \cdot \sqrt {25} + \frac{{\sqrt {196} }}{{\sqrt {49} }}\) bằng
A. 28
B. 22
C.18
D. \(\sqrt 2\)
Câu 5: Tìm x biết \(\sqrt[3]{x} = - 1,5\). Kết quả
A. x = -1,5
B. -3,375
C. 3,375
D. -2,25
Câu 6: Rút gọn biểu thức \(\sqrt[3]{27{{x}^{3}}}-\sqrt[3]{8{{x}^{3}}}+4x\) được
A. 23\(\sqrt[3]{x}\)
B. 23x
C. 15x
D. 5x
Câu 7: Rút gọn biểu thức \(\sqrt{x+4\sqrt{x-4}}+\sqrt{x-4\sqrt{x-4}}\) (điều kiện \(4\le x<8\)) bằng
A. \(2\sqrt{x-4}\)
B. – 4
C. \(2\sqrt{x+4}\)
D. 4
Câu 8: Khử mẫu của biểu thức \(\sqrt{\frac{2}{5{{a}^{3}}}}\) với a>0 được
A. \(\frac{\sqrt{10a}}{5{{a}^{2}}}\)
B. \(\frac{\sqrt{10a}}{5{{a}^{3}}}\)
C. \(\frac{\sqrt{2}}{5{{a}^{2}}}\)
D. \(\frac{2}{5{{a}^{2}}}\)
Câu 9: Rút gọn biểu thức \(\frac{2}{\sqrt{7}-3}-\frac{2}{\sqrt{7}+3}\) được
A. \(\sqrt{7}+3\)
B. \(\sqrt{7}-3\)
C.-6
D. 0
Câu 10: \(\sqrt{9{{x}^{2}}}=12\)
A. x = \(\pm 2\)
B. \(\pm 4\)
C. 2
D. -2
-----Còn tiếp-----
7. Đề thi giữa học kì 1 môn Toán 9 – Số 7
Trường THCS Cẩm Bình
Số câu: 3 câu tự luận
Thời gian làm bài: 45 phút
Năm học: 2021 -2022
8. Đề thi giữa học kì 1 môn Toán 9 – Số 8
Trường THCS Long Điền
Số câu: 10 câu trắc nghiệm, 3 câu tự luận
Thời gian làm bài: 60 phút
Năm học: 2021 -2022
9. Đề thi giữa học kì 1 môn Toán 9 – Số 9
Trường THCS Phan Huy Chú
Số câu: 25 câu trắc nghiệm
Thời gian làm bài: 45 phút
Năm học: 2021 -2022
10. Đề thi giữa học kì 1 môn Toán 9 – Số 10
Trường THCS Phan Bội Châu
Số câu: 4 câu tự luận
Thời gian làm bài: 45 phút
Năm học: 2021 -2022
---Bấm TẢI VỀ hoặc XEM ONLINE để xem đầy đủ nội dung các Đề thi 1-10---