Bài 4: Phương pháp tính các tham số đặc trưng của mẫu
Mời các bạn cùng tham khảo nội dung bài giảng Bài 4: Phương pháp tính các tham số đặc trưng của mẫu sau đây để tìm hiểu về trường hợp số liệu của mẫu cho dưới dạng gồm đủ n giá trị quan sát, trường hợp số liệu của mẫu cho dưới dạng có tấn số ni (nói chung ni > 1).
Mục lục nội dung

Bài 4: Phương pháp tính các tham số đặc trưng của mẫu
Giả sử có mẫu cụ thể WX = (X1, X2,. . . ,Xn), thì trung bình mẫu ¯X và phương sai mẫu (s2) là hai giá trị cơ bản nhất đối với mẫu cụ thể này, s có thể suy ra từ s2; còn f thì tính rất đơn giản. Do đó phần này chúng ta chỉ nêu ra công thức tính ¯x và s2 tương ứng với từng trường hợp số liệu hiện có như sau:
1. Trường hợp số liệu của mẫu cho dưới dạng gồm đủ n giá trị quan sát
Trường hợp này, để tính ¯x ta sử dụng công thức định nghĩa:
¯x=1nn∑i=1xi
Để tính s2 ta dùng công thức:
s2=1n−1[n∑i=1x2i−n(¯x)2]
Chứng minh:
Theo công thức định nghĩa của S2 ta có:
s2=1n−1n∑i=1(xi−¯x)2
Ta có:
(xi−¯x)2=(xi)2−2xi¯x+(¯x)2
Vậy:
n∑i=1(xi−¯x)2=n∑i=1[(xi)2−2¯x.xi+(¯x)2]
=n∑i=1x2i−2¯x.xi+n.(¯x)2=n∑i=1x2i−n.(¯x)2
Suy ra:
S2=1n−1[n∑i=1x2i−n(¯x)2]
Thí dụ 3: Quan sát điểm thi môn Toán cao cấp của 10 sinh viên được chọn ngẫu nhiên từ một lớp ta thu được các số liệu sau:
5; 6; 7; 4; 6; 9; 4; 5; 5; 7
Tính ¯x và s của mẫu này.
Giải
Ta có: 10∑i=1xi=58 vậy: ¯x=5810=5,8
10∑i=1x2i=358 vậy: s2=19[358−10.(5,8)2]=2,4
⇒s=√s2=√2,4=1,549193
Chú ý:
Để tính ¯x ta có thể dùng hàm AVERAGE trong Excel: ¯x=AVERAGE{xi}
Để tính s2 ta có thể dùng hàm VAR trong Excel: s2 =VAR{Xi}
Để tính s ta có thể dùng hàm STDEV trong Excel: s = STDEV{Xi}
Cách thức thực hiện các lệnh này cũng tương tự như lệnh AVERAGE (xem phụ lục 1).
Thí dụ 4: Có các số liệu về doanh số bán (Y) và chi phí chào hàng (X) của 12 công ty thương mại tư nhân cho ỏ bảng dưới đây. Hãy tính trung bình mẫu và độ lệch chuẩn mẫu của X và Y.
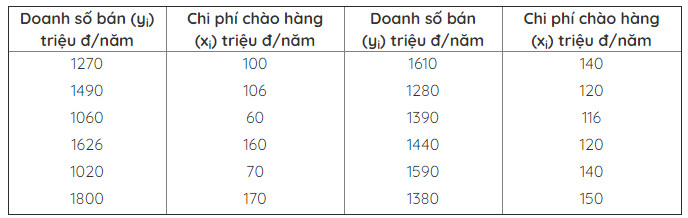
Tính trung bình mẫu và độ lệch chuẩn mẫu của X và Y.
Từ các số liệu cho ở bảng trên, ta tính được:
12∑i=1xi=1452 Vậy: ¯x=145212=121
12∑i=1yi=16956 Vậy: ¯y=1695612=1413
n∑i=1x2i=188192. Vậy: s2X=111[188192−12(121)2]=1136,363636
⇒sX=√1136,363636=33,71
n∑i=1y2i=24549576. Vậy: s2Y=111[24549576−12(1413)2]=53704,36364
⇒sY=√53704,36364=231,742
2. Trường hợp số liệu của mẫu cho dưới dạng có tấn số ni (nói chung ni > 1).
Trường hợp này, để tính ¯x và s2 ta áp dụng công thức:
¯x=1nk∑i=1nixi
s2=1n−1[k∑i=1nix2i−n(¯x)2]
Chú ý: k∑k=1nixi trong công thức (6.30) cũng chính là n∑i=1xi trong công thức (6.27); Tương tự k∑k=1nix2i trong công thức (6.31) cũng chính là n∑k=1x2i trong công thức (6.28).
Với các số liệu cho ở thí dụ 3, ta có thể trình bày số liệu quan sát của mẫu này dưới dạng có tần số như sau:

Từ số liệu ở bảng trên, ta tính được:
k∑i=1nixi=58;k∑i=1nix2i=358
So sánh với kết quả tính ở thí dụ 3 ta có thể minh chứng cho nhận xét nêu trên.
Thí dụ 5: Tính trung bình và phương sai của mẫu cho ở bảng sau:

Giải:
Từ số liệu của mẫu đã cho ta tính được: ∑inixi=314. Vậy: ¯x=31450=6,28
∑inix2i=2144. Vậy: s2=149[2144−50.(6,28)2]=3,5118
Thí dụ 6: Số liệu cho ở cột 1 và cột 3 của bảng dưới đây (bảng 6.33) là số liệu quan sát về lượng hàng bán được (kg/ngày) của một đại lý. Hãy tính trung bình mẫu và phương sai mẫu.
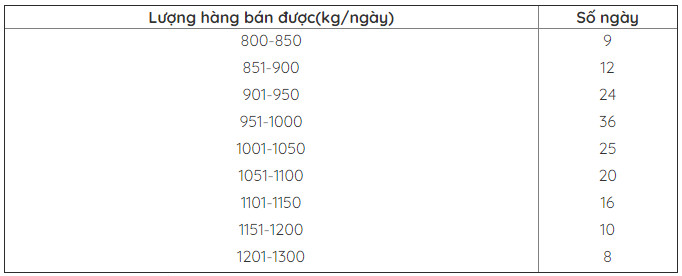
Ta thay mỗi khoảng bằng giá trị trung tâm khoảng, từ đó ta có bảng sau: (bảng 6.34)

Từ số liệu của bảng trên, ta tính được: ∑inixi=162175,5
Vậy:
¯x=162175,5160=1013,596875
n∑i=1nix2i=166159712,75
Vậy
s2=1159[166159712,75−160.(1013,125)2]=11189,51384
Trên đây là nội dung bài giảng Bài 4: Phương pháp tính các tham số đặc trưng của mẫu mà eLib.VN muốn chia sẻ đến các bạn sinh viên. Hy vọng đây sẽ là tư liệu hữu ích giúp các bạn nắm được nội dung bài học tốt hơn. Chúc các bạn học tốt.
Tham khảo thêm
- doc Bài 1: Tổng thể và mẫu
- doc Bài 2: Mô hình xác suất của tổng thể và mẫu
- doc Bài 3: Các tham số đặc trưng của mẫu
- doc Bài 5: Mẫu ngẫu nhiên hai chiều




