Bài 2: Doanh lợi, rủi ro và đường thị trường chứng khoán
Cùng tìm hiểu Doanh lợi dự kiến; Tính toán phương sai của doanh lợi dự kiến; Danh mục đầu tư; Rủi ro, doanh lợi có hệ thống và không có hệ thống; Đa dạng hoá và rủi ro của danh mục đầu tư; Rủi ro có hệ thống và hệ số bêta thông qua nội dung bài giảng Bài 2: Doanh lợi, rủi ro và đường thị trường chứng khoán dưới đây nhé!
Mục lục nội dung
3.1 Trong số của danh mục đầu tư
3.2 Doanh lợi dự kiến của danh mục đầu tư
3.3 Phương sai của danh mục đầu tư
4. Rủi ro, doanh lợi có hệ thống
4.1 Rủi ro có hệ thống và không có hệ thống
4.2 Thành phần doanh lợi có hệ thống
5. Đa dạng hoá và rủi ro danh mục đầu tư
5.3 Đa dạng hoá và rủi ro không có hệ thống
5.4 Đa dạng hoá và rủi ro có hệ thống
6. Rủi ro có hệ thống và hệ số bêta
6.1 Nguyên lý của rủi ro có hệ thống
6.2 Đo lường rủi ro có hệ thống
7. Đường thị trường chứng khoán

Bài 2: Doanh lợi, rủi ro và đường thị trường chứng khoán
Phần trên chúng ta đã trình bày vế doanh lợi, doanh lợi bình quân, cách tính phương sai và độ lệch tiêu chuẩn của doanh lợi. Trong phần này sẽ tập trung nghiên cứu làm thế nào để phân tích doanh lợi và phương sai khi có được thông tin hên quan đến doanh lợi dự kiến và xác suất để đạt được doanh lợi dự kiến đó.
1. Doanh lợi dự kiến
Giả sử: Xem xét hai cổ phần L và U cho thời kỳ là một năm. Dự kiến doanh lợi của cổ phần L cho năm tới là: 25%, dự kiến doanh lợi của cổ phần U cho cùng thời kỳ là: 20%.
Khi các nhà đầu tư đều đồng ý vể doanh lợi dự kiến cho hai loại cổ phần trên thì tại sao vẫn có người muốn chọn cổ phần Ư? Rõ ràng là khi lựa chọn đầu tư vào đâu, các nhà đầu tư có tính đến mức độ rủi ro của nó.
Trong nền kinh tế thị trường, người ta thường quan tâm tới hai tình trạng kinh tế đối lập nhau, đó là: Nền kinh tế ỏ trạng thái hưng thịnh và nền kinh tế suy thoái. Trong năm tới có thể nền kinh tế ỏ trạng thái hưng thịnh trong suốt cả năm, cũng có thế bị suy thoái trong suốt cả năm hoặc cũng có thể một phần của năm sẽ là hưng thịnh và phần còn lại của năm sẽ là suy thoái. Tóm lại, các tình trạng khác nhau của nền kinh tế được xem như là những đại lượng ngẫu nhiên.
Ví dụ 4:
Người ta dự kiến rằng: Ở tình trạng kinh tế hưng thịnh, cổ phần L sẽ có doanh lợi là: 70% và cổ phần U sẽ có doanh lợi là: 10%. Nếu nển kinh tế ở tình trạng suy thoái, cổ phần L sẽ có doanh lợi là: -20% và cổ phần U sẽ có doanh lợi là: 30%.
Giả sử xác suất cho mỗi tình trạng kinh tế kể trên đều là: 0,5. Chúng ta có thể tổng kết bằng bảng sau:
|
Tình trạng của nền kinh tế |
Xác suất xảy ra cho mỗi tình trạng kinh tế |
Doanh lợi dự kiến (%) cho từng tình trạng kinh tế |
|
|
Cổ phần L |
Cổ phần U |
||
|
Suy thoái |
0,5 |
-20 |
30 |
|
Hưng thịnh |
0,5 |
70 |
10 |
|
|
1.0 |
|
|
Nếu ta mua cổ phần u, một nửa thời gian sẽ cho ta doanh lợi là: 30% và nửa thời gian còn lại sẽ cho ta doanh lợi là: 10%. Như vậy, doanh lợi dự kiến cho cổ phần u ký hiệu E (RJ sẽ là:
E (RU) = 0,50 x 30% + 0,50 x 10% = 20%
Nói một cách khác, chúng ta chờ đợi một khoản doanh lợi bình quân là 20% cho suốt thời kỹ xem xét.
Tương tự, doanh lợi dự kiến bình quân cho cổ phần L ký hiệu là: E(RU) sẽ được tính như sau:
E(RJ = 0,50 x (-20%) + 0,50 x 70% = 25%
Đến đây có thế biết rõ: Vì sao cổ phần L có thu nhập dự kiến cao hơn so với cồ phần u mà vẫn có người thích mua cổ phần Ư? Cổ phần L mặc dù có doanh lợi dự kiến cao hơn nhưng độ rủi ro cao hơn. Nếu như sự suy thoái kinh tế xảy ra và kéo dài trong suốt thời kỳ thì cổ phần L bị lỗ 20%, trong khi đó, dù nền kinh tế ở tình trạng nào đi nữa thì cổ phần U vẫn có lãi.
Trong phần trước đã định nghĩa mức bù đắp rủi ro là phần chênh lệch giữa doanh lợi của tài sản rủi ro và doanh lợi của tài sản không có rủi ro. Người ta có thế áp dụng định nghĩa này để tính toán mức bù đắp rủi ro dự kiến như là sự chênh lệch giữa doanh lợi dự kiến của khoản đầu tư có rủi ro và doanh lợi chắc chắn của khoản đầu tư không có rủi ro.
Ví dụ 5:
Doanh lợi của khoản đầu tư không có rủi ro là: 8%; ta gọi 8% là tỷ suất không có rủi ro và ký hiệu là: Rf. Ta có thể' viết công thức tính mức bù đắp rủi ro dự kiến như sau:
Mức bù đắp rủi ro dự kiến = Doanh lợi dự kiến - Tỷ suất không có rủi ro
= E (R) - Rf (5.8)
Sử dụng công thức này, có thể tính mức bù đắp rủi ro dự kiến cho cổ phần L và cổ phần U:
Mức bù đắp rủi ro dự kiến cho cổ phần u = E(Ru) - Rf
= 20% - 8% = 12%
Mức bù đắp rủi ro dự kiến cho cổ phần L = E(Rl) - Rf
= 25% - 8% = 17%
Việc tính toán doanh lợi dự kiến cho cổ phần U và cổ phần L trong trường hợp xác suất xảy ra cho từng tình trạng kinh tế là bằng nhau được tổng kết ở bảng sau:
|
|
|
Cổ phần L |
Cổ phần U |
||
|
(1) |
(2) |
(3) |
(4) |
(5) |
(6) |
|
Tình trạng kinh tế |
Xác suất xảy ra của mỗi tinh trạng kinh tế |
Doanh lợi dự kiến cho từng tinh trạng kinh tế |
Tích số (2) x (3) |
Doanh lợi dự kiến cho từng tinh trạng kinh tế |
Tích số (2) x (5) |
|
Suy thoái |
0,50 |
-0,20 |
-0,10 |
0,30 |
0,15 |
|
Hưng thịnh |
0,50 |
0,70 |
0,35 |
0,10 |
0,05 |
|
|
1,00 |
|
E(RL) = 25% |
|
E(RU) = 20% |
Hãy nghiên cứu một ví dụ khác để hiểu rõ hơn về cách tính doanh lợi dự kiến.
Ví dụ 6
Giả sử người ta tính toán được rằng: Xác suất để xảy tình trạng kinh tế hưng thịnh sẽ kéo dài 20% thời gian xem xét. Hãy xác định doanh lợi dự kiến cho cổ phần u và cổ phần L... Nếu tỷ lệ không có rủi ro là: 10%, hãy tính mức bù đắp rủi ro dự kiến cho từng cổ phần.
Việc tính toán thể hiện ở bảng sau:
|
|
|
Cổ phần L |
Cổ phần U |
||
|
(1) |
(2) |
(3) |
(4) |
(5) |
(6) |
|
Tình trạng kinh tế |
Xác suất xảy ra của mỗi tình trạng kinh tế |
Doanh lợi dự kiến cho từng tình trạng kinh tế |
Tích số (2) x (3) |
Doanh lợi dự kiến cho từng tình trạng kinh tế |
Tích sổ (2) x (5) |
|
Suy thoái |
0.8 |
-0,20 |
-0,16 |
0,30 |
0,24 |
|
Hưng thịnh |
0.2 |
0.70 |
0,14 |
0,10 |
0,02 |
|
|
1,0 |
|
E(RL) = -2% |
|
E(RU) = 26% |
Vì chỉ có hai khả năng có thể xảy ra là: Hưng thịnh và suy thoái. Do vậy, khi biết xác suất xảy ra của tình trạng hưng thịnh là 0,2 thì ta có thể tính được xác suất xảy ra tình trạng suy thoái là: (1 - 0,2 = 0,8).
Mức bù đắp rủi ro của cổ phần u = 26% - 10% = 16%
Mức bù đắp rủi ro của cổ phần L = -2% - 10% = -12%
2. Tính toán phương sai của doanh lợi dự kiến
Để tính toán phương sai của doanh lợi dự kiến cho các khoản đầu tư khác nhau, trước hết ta cần phải xác định các chênh lệch bình phương giữa doanh lợi dự kiến cho từng khoản đầu tư ở mỗi tình trạng kinh tế và doanh lợi dự kiên binh quân. Sau đó ta nhân từng kết quả chênh lệch bình phương đó với xác suất tương ứng của nó. Tổng của các tích số sẽ là phương sai của doanh lợi dự kiến cho khoản đầu tư mà ta đang xem xét. Độ lệch tiêu chuẩn được tính bằng căn bậc hai của phương sai.
Ví dụ 7:
Để minh họa rõ hơn điều vừa nói ở trên, ta tiếp tục lấy cổ phần L và cổ phần u làm ví dụ. Trong trường hợp xác suất xảy ra tình trạng hưng thịnh và suy thoái đều là 0,5. Phương sai của cổ phần u và cổ phần L sẽ là bao nhiêu?
Ta biết, E(RƯ) = 20% và E(Rl) = 25%. Việc tính toán phương sai của hai cổ phần này thể hiện trong bảng sau:
|
(1) |
(2) |
(3) |
(4) |
(5) |
|
Tình trạng kinh tế |
Xác suất xảy ra cùa mỗi tình trạng kinh tế |
Chênh lệch vé doanh lợi của mỗi tinh trạng kinh tế so với doanh lợi bình quân dự kiến |
Bình phương các chênh lệch |
Tích sổ (2) x (4) |
|
Cổ phần L Suy thoái |
0.5 |
-0.20-0,25 = -0.45 |
(-0.45)2 = 0,2025 |
0,10125 |
|
Hưng thịnh |
0.5 |
0,70-0.25 = 0,45 |
(0,45)2 = 0,2025 |
0,10125 |
|
|
|
|
|
σ2L=0,2025 |
|
Cổ phần u Suy thoái |
0.5 |
0,30-0,20= 0,10 |
(0.10)2 = 0.01 |
0,005 |
|
Hưng thịnh |
0,5 |
0,10-0,20 = -0,10 |
(4,10)2 = 0,01 |
0,005 |
|
|
|
|
|
σ2U =0,010 |
Người thấy rằng: Cổ phần L có thu nhập dự kiến bình quân cao hơn cổ phần U, nhưng cổ phần U có độ rủi ro thấp hơn cổ phần L. Nếu chọn cổ phần L có thể đạt được mức doanh lợi là 70% trong điều kiện của nền kinh tế hưng thịnh, tuy nhiên cũng có thể bị lỗ 20% trong điều kiện nền kinh tế lâm vào tình trạng suy thoái. Ngược lại, trong mọi điều kiện thì cổ phần U đều có doanh lợi ít nhất là 10%. Vậy nên mua cổ phần nào? Rất khó trả lời, việc mua cổ phần nào là do sở thích của người mua. Một số người thích đương đầu với rủi ro để hy vọng có được doanh lợi cao hơn nên họ thích mua cổ phần L. Một số người khác không thích liều lĩnh nên họ sẽ chọn mua cổ phần U.
3. Danh mục đầu tư
Danh mục đầu tư là một nhóm các tài sản như là cổ phiếu và trái phiếu do một người đầu tư nắm giữ. Nói chung, các nhà đầu tư thường đầu tư vào nhiều nơi thể hiện bằng nhiều loại cổ phiếu và nhiều loại trái phiếu khác nhau. Trong phần trên đã nghiên cứu rủi ro và doanh lợi của từng tài sản riêng biệt. Trong phần này sẽ tập trung nghiên cứu doanh lợi dự kiến và phương sai của danh mục đầu tư.
3.1 Trong số của danh mục đầu tư
Có nhiều cách khác nhau để diễn tả một danh mục đầu tư, tuy nhiên, cách thuận tiện nhất là hệt kế danh sách của từng khoản đầu tư với giá trị của nó được tính theo tỷ lệ phần tràm so với tổng số tiến đầu tư của một người đầu tư nào đó. Người ta gọi những tỷ lệ phần trăm này là những trọng sô của danh mục đầu tư.
Ví dụ 8
Tổng số tiền đầu tư của một người đầu tư nào đó là 200 đv, anh ta đầu tư vào một loại tài sản với số tiền là ÕO đv, còn lại 150 đv anh ta đầu tư vào một tài sản khác. Vậy, trọng số danh mục đầu tư cho tài sản thứ nhất là: 50/200 = 0,25. Trọng số danh mục đầu tư cho tài sản thứ hai là: 150/200 = 0,75. Nếu danh mục đầu tư bao gồm một trảm loại tài sản khác nhau sẽ có một trăm trọng số cho danh mục đầu tư đó. Tuy nhiên, cần lưu ý rằng: Tổng của tất cả các trọng số của danh mục đầu tư bao giờ cũng bằng 1.
3.2 Doanh lợi dự kiến của danh mục đầu tư
Ví dụ 9
Trở lại cổ phần u và cổ phần L, nếu dùng một nửa số tiền đầu tư vào cổ phần U và một nửa số tiền còn lại đầu tư vào cổ phần L, trong điều kiện xác suất xảy ra cho tình trạng kinh tế hưng thịnh và suy thoái là như nhau và bằng 0,5. Vậy, doanh lợi dự kiến cho danh mục đầu tư là bao nhiêu?
Giả sử, nền kinh tế lâm vào tình trạng suy thoái suốt thời kỳ xem xét, một nửa số tiền đầu tư vào cổ phần L sẽ bị lỗ 20%, một nửa số tiền còn lại đầu tư vào cổ phần U sẽ có lãi là 30%. Như vậy, doanh lợi của danh mục đầu tư (ký hiệu là Rp) sẽ được tính như sau:
Rp = 0,5 x (-20%) + 0,5 x 30% = 5%
Nếu nển kinh tế hoàn toàn hưng thịnh trong suốt thời gian xem xét, ta có:
Rp = 0,5 x 70% + 0,5 x 10% = 40%
Nhưng xác suất xảy ra tình trạng kinh tế suy thoái và hưng thịnh là như nhau và bằng 0,5. Do đó, doanh lợi dự kiến cho danh mục đầu tư của ta (được ký hiệu là E(Rp) sẽ là:
E(Rp) = 0,5 x 5% + 0,5 x 40% = 22,5%
Trong phần trước đã nghiên cứu cách tính doanh lợi dự kiến cho từng loại tài sản riêng biệt như là cho cổ phần U cho ta E(RU) và cổ phần L cho ta E(RU). Để tính doanh lợi dự kiến cho danh mục đầu tư một cách nhanh chóng hơn và trực tiếp hơn, ta có thể lấy trọng số của từng loại tài sản riềng biệt trong danh mục đầu tư nhân (x) với doanh lợi dự kiến của tài sản đó. Cộng tất cả các tích số đó lại với nhau ta sẽ có doanh lợi dự kiến của danh mục đầu tư.
Ở ví dụ 4, ta đã tính được doanh lợi dự kiến của cổ phần U là: E(RU) = 20% và doanh lợi dự kiến của cổ phần L là: E(RL) = 25%, theo điều kiện nêu ra ở ví dụ 9, trọng số của cổ phần U và cổ phần L đều là 0,5. Ta tính được doanh lợi dự kiến cho danh mục đầu tư như sau:
E(Rp) = 0,5 x E(RL) + 0,5 x E(RU)
= 0,5 x 25% + 0,5 x20% = 22,5%
Cách tính toán này không phụ thuộc vào việc có bao nhiêu loại tài sản trong danh mục đầu tư. Giả sử danh mục đầu tư của ta có n tài sản, X| là trọng số của tài sản i. Vậy, công thức chung để tính doanh lợi dự kiến cho danh mục đầu tư sẽ được viết như sau:
E(Rp) = X1 x E(R1) + X2 x E(R2) + ... + Xn x E(Rn) = ∑XiE(Ri) (5.9)
Với: i = 1, 2, 3,... n
3.3 Phương sai của danh mục đầu tư
Ví dụ 10
Để trình bày một cách ngắn gọn, tiêp tục lấy cồ phần U và cổ phần L làm ví dụ. Trên đây, ta đã tính được rằng: nêu nền kmh tế hoàn toàn rơi vào tình trạng suy thoái trong suốt thời kỳ nghiên cứu thì doanh lợi dự kiến cho danh mục đầu tư là: 5%, nếu nền kinh tế hưng thịnh trong suốt thời kỳ nghiên cứu thi doanh lợi dự kiến cho danh mục đầu tư sẽ là: 40%. Trong điều kiện xác suất xảy ra cho cả hưng thịnh và suy thoái đều là 0,5 ta đã tính được E(Rp) = 0,225. Vậy, phương sai và độ lệch tiêu chuẩn của danh mục đầu tư là bao nhiêu?
Việc tính toán phương sai và độ lệch tiêu chuẩn của danh mục đầu tư được tổng kết ở bảng sau:
|
(1) |
(2) |
(3) |
(4) |
(5) |
|
Tình trạng kinh tế |
Xác suất xảy ra của mỗi tình trạng kinh tế |
Doanh lợi của danh mục dầu tư cho mỗi tình trạng kinh tế |
Bình phương các chênh lệch giữa doanh lợi theo từng tinh trạng kinh tế và doanh lợi dự kiến binh quân của danh mục đầu tư |
Tích sổ (2) x (4) |
|
Suy thoải |
0,5 |
5% |
(0,05 - 0.225)2 = 0,30625 |
0,0153125 |
|
Hưng thịnh |
0,5 |
40% |
(0,40 - 0,225)2 = 0,30625 |
0,0153125 |
|
|
|
|
|
σ2P=0,030625 |
|
σP=√0,030625=17,5% |
||||
Ví dụ 11
Giả sử thay đối các trọng số của danh mục đầu tư 2/11 số tiền dùng để đầu tư vào cổ phần L và số tiền còn lại 9/11 dùng để đầu tư vào cổ phần U. Trong điều kiện nền kinh tế suy thoái trong suốt thời kỳ nghiên cứu, doanh lợi dự kiến cua danh mục đầu tư được xác dinh như sau:
Rp = (2/11) x (-20%) + (9/11) x (30%) = 20,91%
Trong điều kiện nền kinh tế hưng thịnh suốt thời kỳ xem xét, doanh lợi dự kiến của danh mục đầu tư được xác định như sau:
Rp = (2/11) x (70%) + (9/11) x (10%) = 20,91%
Như vậy, nếu bổ trí danh mục đầu tư theo các trọng số như trên thì dù nền kinh tế ở trạng thái nào đi nữa, vẫn có doanh lợi dự kiến là 20,91%. Không cần phải tính toán, ta có thể thấy là: trong trường hợp này phương sai của danh mục đầu tư bằng 0. Điều này rất quan trọng cho việc bố trí một danh mục đầu tư sao cho có thể loại bỏ được một số rủi ro nhất định. Vấn đề này sẽ được bàn kỹ ở những phần sau.
4. Rủi ro, doanh lợi có hệ thống và không có hệ thống
4.1 Rủi ro có hệ thống và không có hệ thống
Rủi ro có hệ thông là loại rủi ro tác động đến toàn bộ hoặc hầu hết các tài sản. Vì thế người ta còn gọi nó là rủi ro của thị trường. Như đã thấy, sự bấp bênh của các điều kiện kinh tế chung như việc giảm GDP, tăng lãi suất tiền vay, tăng tốc độ lạm phát... là những ví dụ cho rủi ro có hệ thông. Những điều kiện này tác động đến hầu hết các doanh nghiệp.
Rủi ro không có hệ thống là loại rủi ro chỉ tác động đến một tài sản hoặc một nhóm nhỏ các tài sản, nghĩa là loại rủi ro này chỉ liên quan tới từng doanh nghiệp cụ thể nào đó. Vì thể ngưòi ta còn gọi là rủi ro đơn nhất hay rủi ro cho một tài sản cụ thế. Chẳng hạn, sự bãi công cùa công nhân thuộc doanh nghiệp A sẽ chỉ ảnh hưởng đến sản suất kinh doanh của doanh nghiệp A, đối khi nó cũng có ảnh hương chủt ít đến một vài doanh nghiệp khác đang có một số hợp đồng mua bán với doanh nghiệp này. Các doanh nghiệp không có liên quan tói doanh nghiệp A thì hoàn toàn không bị tác động.
4.2 Các thành phần doanh lợi có hệ thống và không có hệ thống
Khi ta dự kiến doanh lợi cho một khoản đầu tư nào đó, có những khoản không dự kiến được. Trong quá trình thực hiện, doanh lợi có thể tăng lên hoặc giảm đi so với dự kiến. Nếu ta ký hiệu phần tăng lên hoặc giảm đi đó là U, ta có thể viết công thức tính doanh lợi như sau:
R = E(R) + U
Trong đó:
R - Doanh lợi đạt được
E(R) - Doanh lợi dự kiến
U - Doanh lợi không dự kiến được.
Như ở phần trên, ta thấy: Có hai loại rủi ro, rủi ro có hệ thống và rủi ro không có hệ thống. Phần doanh lợi không dự kiến được là do hai loại rủi ro này gây ra. Ta cũng có thể chia bộ phận doanh lợi không dự kiến được thành hai phần, phần thứ nhất là phần không có hệ thống và do rủi ro không có hệ thống gây ra, ta ký hiệu phần này là ε. Phần thứ hai là phần có hệ thông do rủi ro có hệ thốhg gây ra và được ký hiệu là m. Đến đầy, ta có thể viêt công thức tính doanh lợi đạt được là:
R=E(R)+m+ε (5.11)
Việc phân chia bộ phận doanh lợi không dự kiến được thành hai phần là rất quan trọng. Để thây được tại sao nó quan trọng, chúng ta sẽ nghiên cứu ỏ phần sau đây nói vể rủi ro của danh mục đầu tư.
5. Đa dạng hoá và rủi ro của danh mục đầu tư
5.1 Tác động của đa đạng hoá
Khi ta có một lượng tiền nào đó, nếu ta dùng toàn bộ số tiền để đầu tư vào một loại tài sản thì mức độ rủi ro cao hơn là việc đầu tư sô tiền này vào nhiều tài sàn khác nhau.
Để thấy được mối quan hệ giữa cách bổ' trí một danh mục đầu tư và rủi ro của danh mục đầu tư, chúng ta hãy nghiên cứu bảng trang 143.
Qua bảng ta thấy rằng: Độ lệch tiêu chuẩn cho danh mục đầu tư có một cổ phần là 49,24%. Điều này có nghĩa là nếu ta lựa chọn một cách ngẫu nhiên một loại cổ phần của một doanh nghiệp nào đó và đầu tư toàn bộ số tiền của ta vào đó thì độ lệch tiêu chuẩn của doanh lợi sẽ là 49,24% cho một năm. Nếu ta lựa chọn một cách ngẫu nhiên hai loại cổ phần và đầu tư vào mỗi loại một nửa số tiền thì độ lệch tiêu chuẩn bình quân sẽ là 37,36% v.v...
Điều quan trọng rút ra ở đây là: độ lệch tiêu chuẩn giảm khi mà số lượng các loại cổ phần tăng lên. Nếu ta lựa chọn một cách ngẫu nhiên 100 loại cổ phần khác nhau thì độ lệch tiêu chuẩn bình quân của danh mục đầu tư sẽ giảm xuống 19,69%. Nêu ta lựa chọn một cách ngẫu nhiên 500 cổ phần khác nhau thì độ lệch tiêu chuẩn bình quân sẽ là 19,27%. Nếu ta tiếp tục tăng thểm số lượng cổ phần cho danh mục đầu tư của ta thì ta thấy kết quả giảm của độ lệch tiêu chuẩn rất nhỏ hoặc không thay đối.
|
(1) Số lượng các cổ phần khác nhau của một danh mục đầu tư |
(2) Độ lệch tiêu chuẩn bình quân của doanh lợi hàng năm cửa danh mục đầu tư |
(3) Tỷ lệ giữa độ lệch tiêu chuẩn của danh mục đầu tư so với độ lệch tiêu chuẩn của việc dầu tư vào một cổ phần |
|
1 |
49,24% |
1,00 |
|
2 |
37,36 |
0,76 |
|
4 |
29,69 |
0,60 |
|
6 |
26,64 |
0,54 |
|
8 |
24,98 |
0,51 |
|
10 |
23,93 |
0,49 |
|
20 |
21,68 |
0,44 |
|
30 |
20,87 |
0,42 |
|
40 |
20,46 |
0,42 |
|
50 |
20,20 |
0,41 |
|
100 |
19,69 |
0,40 |
|
200 |
19,42 |
0,39 |
|
300 |
19,34 |
0,39 |
|
400 |
19,29 |
0,39 |
|
500 |
19,27 |
0,39 |
|
1000 |
19,21 |
0,39 |
Nguồn: Tạp chí phân tích lượng và tài chính 22/9/1987, số: 353-64 Nhan đề: "Bao nhiêu cổ phần sẽ tạo nên một danh mục đấu tư đa dạng hóa"
5.2 Nguyên lý của da dạng hoá
Từ bảng trên có thể vẽ được đồ thị sau đây:
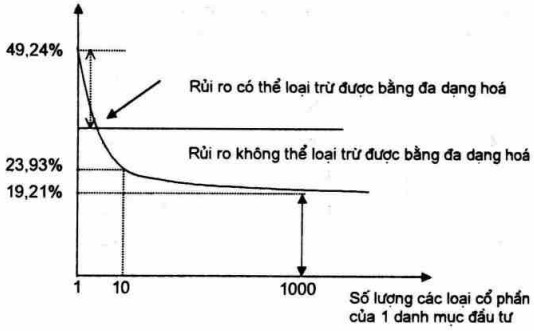
Nhìn vào đồ thị, ta thấy có hai điểm cần lưu ý:
Thứ nhất, một số rủi ro có liên quan đến từng loại tài sản có thể bị loại trừ bằng cách bố trí danh mục đầu tư. Quá trình bố trí danh mục đầu tư được tiến hành bằng cách dàn trải việc đầu tư vào nhiều loại tài sản khác nhau được gọi là đa dạng hoá.
Nguyên lý của đa dạng hoá cho thấy rằng: Dàn trải việc đầu tư vào nhiều tài sản khác nhau sẽ loại trừ được một số rủi ro. Phần diện tích trên hình vẽ ký hiệu "rủi ro có thể loại trừ bằng đa dạng hoá" chính là bộ phận rủi ro có thể loại trừ thông qua đa dạng hoá.
Thứ hai, cùng rất quan trọng,là sẽ có một mức tới thiểu của rủi ro mà không thế loại trừ nó bằng việc đa dạng hoá.
Mức tới thiểu này được thể hiện trên hình vẽ với ký hiệu: "rủi ro không thể loại trừ bằng đa dạng hoá". Hai điếm này cho ta kết luận rằng: Đa dạng hoá có thể làm giảm rủi ro, nhưng việc giảm này chỉ có thể đạt đến một điểm nhát định chứ không thể giảm mãi.
5.3 Đa dạng hoá và rủi ro không có hê thống
Trên đây người ta đã khang định: Một số rủi ro có thể loại trừ bằng đa dạng hoá, một số rủi ro khác thì không thể loại trừ được theo cách này. Sẽ có một câu hỏi là: tại sao lại như vậy? Cần nhố lại phần trước đây nói về rủi ro có hệ thông và rủi ro không có hệ thổng. Theo định nghĩa, rủi ro không có hệ thống là rủi ro chỉ liên quan đến một hoặc một vài tài sản. Chẳng hạn, nếu xem xét một loại cổ phần của một doanh nghiệp nào đó, dự án về chế tạo sản phẩm mới hoặc sự tiết kiệm do cải tiến quy trình công nghệ có thể mang lại giá trị thuần tuý dương và do đó có thể làm tăng giá trị cổ phần của doanh nghiệp. Ngược lại, nếu doanh nghiệp phạm pháp và phải đền bù bằng một lượng tiền đáng kể, hoặc do sự cổ bất ngờ gây thiệt hại cho doanh nghiệp, hoặc do bãi công của công nhân trong doanh nghiệp v.v... có thể dẫn đến giảm giá trị cổ phần của doanh nghiệp.
Đến đây có thể nhận thấy rằng: nếu chỉ đầu tư vào một loại cổ phần của một doanh nghiệp nào đó thì nghĩa là kết quả đầu tư bị phụ thuộc rất nhiều vào những sự kiện xảy ra đối với doanh nghiệp. Nếu đầu tư vào nhiều loại tài sản ở nhiều doanh nghiệp khác nhau thì sự phụ thuộc này giảm đi nhiều, bởi vì nêu chẳng may bị lỗ ở doanh nghiệp này thì vẫn có lãi ở doanh nghiệp khác. Việc bù trừ đó sẽ làm cho rủi ro của danh mục đầu tư giảm đi.
Như vậy, rủi ro không có hệ thông sẽ bị loại trừ thông qua việc đa dạng hoá. Vì vậy, một danh mục đầu tư với số lượng lớn các tài sản khác nhau có thế dẫn đến một điều là: rủi ro không có hệ thống của nó bằng 0. Trên thực tế, khái niệm "có thế đa dạng hoá" và khái niệm "rủi ro không có hệ thông" có thể sử dụng thay thế cho nhau.
5.4 Đa dạng hoá và rủi ro có hệ thống
Rủi ro có hệ thốhg không thể loại trừ bằng cách đa dạng hoá, bởi vì theo định nghĩa, rủi ro có hệ thổng tác động đến tất cả các loại tài sản khác nhau. Vì lẽ đó, cho dù ta có tới bao nhiêu loại tài sản khác nhau trong một danh mục đầu tư đi nữa thì cũng không loại trừ được rủi ro có hệ thống. Vì vậy trên thực tế, khái niệm "không thể đa dạng hoá" và khái niệm "rủi ro có hệ thống" có thể sử dụng thay thế cho nhau.
6. Rủi ro có hệ thống và hệ số bêta
Trong mục này sẽ nghiên cứu để trả lời câu hỏi: cái gì quyết định mức bù đắp rủi ro cho một tài sản có rủi ro? Hay nói một cách khác: Tại sao mức bù đắp rủi ro của tài sản này lại cao hơn mức bù đắp rủi ro của tài sản khác? Việc trả lời câu hỏi này chủ yếu dựa vào sự khác biệt giữa rủi ro có hệ thông và rủi ro không có hệ thống.
6.1 Nguyên lý của rủi ro có hệ thống
Đến đây đã nhận thấy rằng: Tổng số rủi ro liên quan đến một tài sản bao gồm hai bộ phận: Rủi ro có hệ thông và rủi ro không có hệ thốhg. Chúng ta cũng đã nhận thức được là: Rủi ro không có hệ thông có thể bị loại trừ thông qua việc đa dạng hoá. Ngược lại, chúng ta không thể loại trừ được rủi ro có hệ thông bằng cách đa dạng hoá.
Dựa trên cơ sở nghiên cứu trên, chúng ta thấy: cần phải xác định chính xác rủi ro nghĩa là gì? Nguyên lý của rủi ro có hệ thống đã chỉ ra rằng: Phần thướng trao cho việc chịu đựng rủi ro chỉ phụ thuộc vào rủi ro có hệ thông của khoản đầu tư. Rủi ro không có hệ thông có thể loại trừ thông qua việc đa dạng hoá mà không cần có chi phí, vì vậy sẽ không có phần thưởng cho loại rủi ro này. Hay nói một cách khác, thị trường sẽ không đền bù cho loại rủi ro không cần thiết phải sinh ra.
Nguyên lý của rủi ro có hệ thông khẳng định: Doanh lợi dự kiến cho một tài sản chỉ phụ thuộc vào rủi ro có hệ thông. Nghĩa là, chì riêng rủi ro có hệ thống là loại rủi ro có liên quan đến việc quyết định mức doanh lợi dự kiến và mức bù đắp rủi ro của một tài sản.
6.2 Đo lường rủi ro có hệ thống
Rủi ro có hệ thông là một trong những yếu tố quyết định mức doanh lợi dự kiến của một tài sản, vi thế cần biết cách đo mức độ rủi ro có hệ thông cho các khoản đầu tư khác nhau. Thước đo mà chúng ta sẽ sử dụng là hệ số bêta ß.
Hệ số ß cho ta biêt mức rủi ro có hệ thống của một tài sản cụ thể so với mức rủi ro có hệ thông bình quân của một tài sản là bao nhiêu? Theo định nghĩa này, một tài sản nào đó có ß = 0,5 thì có nghĩa là: mức rủi ro có hệ thống của tài sản này bằng một nửa so với mức rủi ro bình quân cho một tài sản, nếu một tài sản có ß = 2 thì có nghĩa là: mức rủi ro có hệ thống của tài sản này bằng hai lần so với mức rủi ro bình quân cho một tài sản v.v...
6.3 Bêta của danh mục đầu tư
Ví dụ 12:
Giả sử ta có thông tin về một số chứng khoán của các doanh nghiệp khác nhau với các hệ số bêta thể hiện ở bảng sau đây:
|
(1) cổ phần của các doanh nghiệp |
(2) Hệ số p |
|
Doanh nghiệp K |
0,75 |
|
Doanh nghiệp M |
0,70 |
|
Doanh nghiệp L |
1,05 |
|
Doanh nghiệp o |
0,99 |
|
Doanh nghiệp p |
1,01 |
|
Doanh nghiệp Q |
0,64 |
|
Doanh nghiệp R |
1,16 |
|
Doanh nghiệp s |
1,42 |
Bêta của danh mục đầu tư có thể’ được tính toán giống như tính toán doanh lợi dự kiến của danh mục đầu tư. Theo sô liệu ở bảng trén, giả sử có một số tiền nào đó, người ta đầu tư một nửa sô tiền vào cổ phần của doanh nghiệp o và một nửa còn lại được đầu tư vào doanh nghiệp R. Vậy p của danh mục đầu tư là bao nhiêu?
βP=0,50×βo+0,50×βR=0,50×0,99+0,55×1,16=1,075
Nói chung, để tính ß cho một danh mục đầu tư, ta lấy từng trọng số của danh mục đầu tư nhân với ß tương ứng với tài sản đó. Sau cùng ta cộng tất cả các tích sô đó lại, sẽ có ß của danh mục đầu tư.
7. Đường thị trường chứng khoán
Trong phần này chúng ta hãy xem rủi ro sẽ được đền bù trên thị trường như thế nào?
7.1 Bêta và mức bù đắp rủi ro
Ví dụ 13:
Giả sử rằng: Tài sản A có thu nhập dự kiên E(RA) = 20% và ßA = 1,6. Tỷ suất không có rủi ro là Rf = 8%. Lưu ý rằng tài sản không có rủi ro là tài sản không có rủi ro có hệ thông (thậm chí không có cả rủi ro không có hệ thống), vì vậy tài sản không có rủi ro sẽ có ß = 0.
Nếu ta bổ' trí một danh mục đầu tư gồm có tài sản A và tài sản không có rủi ro, ta có thể tính toán được một vài phương án doanh lợi dự kiến khác nhau và các hệ số ß khác nhau. Chẳng hạn nếu ta đầu tư 25% vào tài sản A thì thu nhập dự kiến sẽ là:
E(RP) = 0,25 x E(RA) + (1 - 0,25) x Rf
= 0,25 x 20% + 0,75 x 8% = 11%
Tương tự, ß của danh mục đầu tư sẽ là:
βP=0,25×βA+(1−0,25)×0=0,25×1,6=0,4
Lưu ý rằng: Tổng các trọng số của một danh mục đầu tư bao giờ cũng bằng 1. Do vậy, trong danh mục đầu tư này, 25% đầu tư vào tài sản A thì có nghĩa là 75% sẽ được đầu tư vào tài sản không có rủi ro.
Có một điều phân vân là: Liệu tỷ lệ đầu tư vào tài sản A có khả năng vượt quá 100% hay không? Câu trả lời ở đây là có. Điều này có thể xảy ra với nhà đầu tư khi mà anh ta đi vay tiền tại tỷ suất không có rủi ro. Ví dụ, nhà đầu tư có 100 đv, anh ta đi vay thểm 50 đv nữa tại lãi suất 8% là tỷ suất không có rủi ro. Như vậy, tổng số đầu tư vào tài sản A là 150 đv. Hay có thể nói nhà đầu tư này đã đầu tư 150% vốn so với vốn của riêng anh ta. Trong trường hợp này thu nhập dự kiến sẽ là:
E(RP) = 1,50 x E(RA) + (1 - 1,50) x Rf
= 1,50 x 20% - 0,50 x 8% = 26%
Hệ số p của danh mục đầu tư sẽ là:
βP=1,50×βA+(1−1,50)×0=1,50×1,6=2,4
Tương tự như vậy, có thế tính toán được một số phương án khác và liệt kế ở bảng sau đây:
|
Trọng sô của tài sản A trong danh mục đầu tư |
Doanh lại dư kiến của danh mục đầu tư E(RP) |
Bêta của danh mục đầu tư (βP) |
|
0% |
8% |
0,0 |
|
25% |
11% |
0.4 |
|
50% |
14% |
0,8 |
|
75% |
17% |
1.2 |
|
100% |
20% |
1.6 |
|
125% |
23% |
2,0 |
|
150% |
26% |
2.4 |
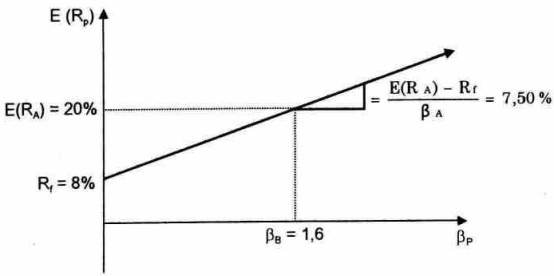
Nhìn vào đồ thị trên ta thấy: nếu di chuyển từ điểm mà tài sản A không có rủi ro với PA = 0 tới điểm mà tại đó βA = 1,6 thì đồng thời với việc tăng bêta, doanh lợi dự kiến cho danh mục đầu tư cũng tăng từ 8% lên 20%.
Nhưng ta biết, E(RA) - Rf = 20% - 8% = 12% được gọi là mức bù đắp rủi ro của tài sản A. Có thể tính được độ dốc của đường thẳng này bằng cách lấy mức bù đắp rủi ro của tài sản A chia cho hệ số bêta của nó.
Độ dốc tài sản A = E(RA)−R1βA=20%−8%1,6=7,50% (5.12)
Độ dốc của tài sản nói lên rằng: Tài sản A đề nghị được đền bù rủi ro với tỷ suất 7,5%. Nói cách khác, tài sản A có mức bù đắp rủi ro là 7,50% cho một đơn vị rủi ro có hệ thống.
Ví dụ 14:
Giả định là có một tài sản khác, tài sản B. Tài sản này có bêta = 1,2 và doanh lợi dự kiến là 16%. Vậy đầu tư vào tài sản nào thì tôt hơn? Tài sản A hay tài sản B? Thực sự là rất khó trả lời. Một số người thích đầu tư vào tài sản A, còn một sở người khác lại thích đầu tư vào tài sản B. Tuy nhiên, để có thế trả lời được rằng: nên đầu tư vào tài sản nào thì cần xác định thểm một số thông tin về tài sản B thông qua việc tính toán sau đây: Cùng làm giông như đối với tài sản A ỏ trên. Ta tính toán một số phương án thích hợp giữa thu nhập dự kiến và bêta của danh mục đầu tư bao gồm tài sản B và tài sản không có rủi ro. Chẳng hạn, nêu ta đầu tư 25% sô tiền vào tài sản B thì nghĩa là 75% số tiền còn lại sẽ được đầu tư vào tài sản không có rủi ro. Doanh lợi dự kiến của danh mục đầu tư sẽ là:
0,25 x E(RB) + 0,75 x Rf = 0,25 x 16% + 0,75 x 8% = 10%
Tương tự, bêta của danh mục đầu tư ßp sẽ là:
βP=0,25×βB+0,75×0=0,25×1,2=0,30
Tương tự làm như vậy ta sẽ có bảng sau đây:
|
Trong số của tài sản B trong danh mục đẩu tư |
Doanh lợi dư kiến của danh muc dầu tư E (RP) |
Bê ta của danh mục đầu tư (βP) |
|
0% |
8% |
0,0 |
|
25% |
10% |
0,3 |
|
50% |
12% |
0.6 |
|
75% |
14% |
0,9 |
|
100% |
16% |
1.2 |
|
125% |
18% |
15 |
|
150% |
20% |
1,8 |
Độ dốc = E(RB)−R1βB=16%−8%1,2=6,67%
Từ bảng trên có thể vẽ được đồ thị sau đây:
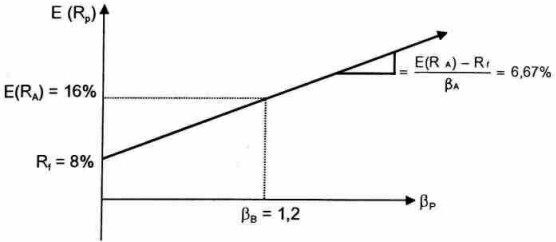
Dựa trên các thông tin trên đây có thể nói rằng: Đầu tư vào tài sản A tốt hơn là đầu tư vào tài sản B, bởi vì tài sản B để nghị mức bù đắp rủi ro không đủ cho mức rủi ro có hệ thống của nó nếu so với tài sản A. Để thây rõ hơn, hãy so sảnh tài sản A và tài sản B trên cùng một đồ thị sau đây:
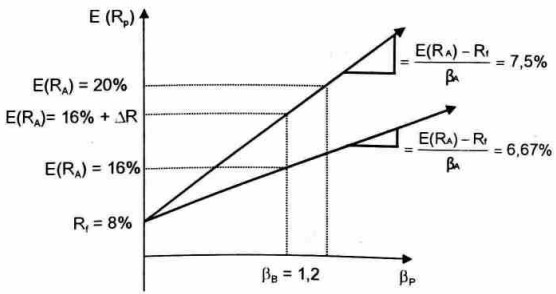
Đồ thị trên cho thấy: Đường thẳng biểu thị sự kết hợp giữa doanh lợi dự kiến và p của tài sản A nằm cao hơn so với đường thẳng biểu thị doanh lợi dự kiến và p của tài sản B. Điều này có thể nhận biết dễ dàng ngay cả trong trường hợp không có đồ thị thông qua sự khác biệt về độ dốc của hai đường thẳng này (7,50% > 6,67%). Sự khác biệt cho biết: Với bất kỳ mức rủi ro có hệ thống nào cho trước (được đo bằng P) thì tài sản A cũng có mức doanh lợi cao hơn so với tài sản B. Nhìn vào đồ thị, giả sử p = 1,2 ta có: E(Rß) = 16% trong khi đó E(Ra) = 16% + AR.
Với nhận xét như trên, có thế gợi ý cho nhà đầu tư rằng anh ta nên đầu tư vào tài sản A.
Tuy nhiên tình trạng của tài sản A và tài sản B như đâ miêu tả trên đây không thể kéo dài mải trên thị trường vốn, bởi vì các nhà đầu tư đổ xô đầu tư vào tài sản A và hầu như không có ai đầu tư vào tài sản B nên sẽ xảy ra tình trạng: Giá của tài sản A sẽ tàng lên và giá của tài sản B sẽ bị hạ thấp. Như đã biết, giá của tài sản và doanh lợi dự kiến của nó vận động ngược chiểu nhau, do vậy doanh lợi của tài sản A sẽ giảm đi và doanh lợi của tài sản B sẽ tăng lên. Việc mua và bán hai loại tài sản này tiếp tục diễn ra cho đến khi cả hai tài sản này cùng nằm trên một đường thẳng. Điều đó có nghĩa là: cả hai loại tài sản này cùng để nghị một mức đền bù về sự chịu đựng rủi ro. Nói cách khác, trên thị trường cạnh tranh ta có:
E(RA)−RfβA=E(RB)−RfβB
Đây là môi quan hệ cơ bản giữa rủi ro và doanh lợi. Trên đây lấy hai tài sản làm ví dụ, cách lập luận trên có thể mở rộng cho nhiều loại tài sản khác nhau tương tự như cách làm trên. Trên thực tế, dù có bao nhiêu tài sản đi nữa thì các tài sản này cũng phải vận động theo hưống là có cùng một tỷ suất bù đắp rủi ro. Giả sử tài sản này có mức rủi ro có hệ thông gấp đối tài sản khác thì mức bù đắp rủi ro cho tài sản này nhất định phải gấp đối so với tài sản khác. Do các tài sản trên thị trường phải có cùng tỷ suất bù đắp rủi ro nên chúng phải được vẽ trên cùng một đường thẳng. Điều này có thể được minh hoạ bằng đồ thị sau:
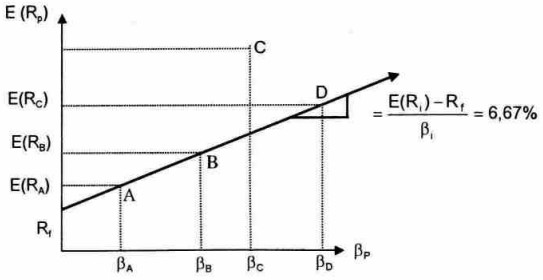
Như đã chỉ ra trên đồ thị, tài sản A và tài sản B được vẽ trực tiếp trên đường thẳng, vì vậy chúng có tỳ suất đền bù rủi ro như nhau. Nếu có một tài sản nào đó nằm phía trên đường thẳng này, ví dụ như tài sản c thì giá trị của tài sản c nhất định sẽ tăng lên và doanh lợi dự kiến của nó sẽ giảm cho đến khi nằm vào đưòng thẳng. Tương tư như vậy, nếu có một tài sản nào đó nằm phía dưới đường thẳng này, ví dụ như tài sản D thì giá của nó nhất định sẽ giảm đi và doanh lợi dự kiến của nó sẽ tăng lên cho đến khi nằm vào đường thẳng. Trên thị trường vốn, hiện tượng như tài sản c thi được gọi là giá cả cao hơn giá trị của nó. Còn hiện tượng như tài sản D thì được gọi là giá cả thấp hơn giá trị của nó. Đây là quan điểm rất quan trọng để kiểm nghiệm các thị trường tài chính.
7.2 Đường thị trường chứng khoán
Đường thẳng được vẽ như trên cho mọi tài sản trên thị trường tài chính là rất quan trọng. Đường thắng thể hiện mối quan hệ giữa rủi ro có hệ thống và doanh lợi dự kiến được gọi là đường thị trường chứng khoán (SML). Trong tài chính doanh nghiệp, quan điểm về giá trị hiện tại thuần tuý (NPV) được coi là quan trọng nhất, kế theo đó là đường SML.
Do SML có tầm quan trọng như vậy, nên cần tìm cách để biết được phương trình của nó. Giả sử bố trí một danh mục đầu tư với toàn bộ các loại tài sản của thị trường. Một danh mục đầu tư như vậy được gọi là danh mục dầu tư của thị trường. Doanh lợi dự kiến của nó được viết là E(RM).
Do tất cả các tài sản trên thị trường phải được vẽ trên đường SML, vì thể danh mục đầu tư của thị trường phải bao gồm tất cả các tài sản đó. Đế xác định xem có thể vẽ đường SML như thể nào, trước hết cần phải xác định cho được hệ sô p cho danh mục đầu tư của thị trường (βM). Do danh mục đầu tư này đại diện cho tất cả các tài sản trên thị trường, nên chắc chắn rằng danh mục đầu tư này có mức rủi ro bình quân có hệ thông, hay nói một cách khác, βM=1. Đến đây có thể biết được độ dốc của đường SML như sau:
Độ dốc của SML = E(RM)−RfβM=E(RM)−Rf1=E(RM)−Rf
E(RM) - Rf được gọi là mức bù đắp rủi ro của thị trường bởi vì nó là mức bù đắp rủi ro cho danh mục đầu tư của thị trường.
Gọi E(R¡) và βi là doanh lợi dự kiến và bêta của một danh mục đầu tư bất kỳ nào đó trên thị trường. Ta biết rằng danh mục đầu tư này phải được vẽ trên đường SML vì nó phải có cùng tỷ suất đền bù rủi ro giông như các tài sản khác trên thị trường. Vậy ta có thể biết:
E(Ri)−Rfβi=E(RM)−Rf
Nếu viết lại, ta sẽ có: E(Ri)=Rf+βi[E(RM)−Rf] (5.14)
Công thức trên được gọi là mô hình định giá tài sản viết tắt là: CAPM.
CAPM chỉ ra rằng: Doanh lợi dự kiến của một tài sản cụ thể nào đó phụ thuộc vào ba yếu tố:
Yếu tố thứ nhất, đó là giá trị thời gian thuần tuý của tiền được đo bằng tỷ suất không có rủi ro Rf. Tỷ suất này đơn thuần chỉ đền bù cho sự chờ đợi tiền của nhà đầu tư và không hể có rủi ro
Yếu tố thứ hai, là sự đền bù cho rủi ro có hệ thống được đo bằng mức rủi ro của thị trường [E(RM) - Rf].
Yếu tố thứ ba, là mức rủi ro có hệ thống được đo bằng ß;, đây là mức rủi ro có hệ thông cho từng tài sản cụ thể.
7.3 Mối liên hệ giữa đường thị trường chứng khoán và chi phí của vốn
Đường thị trường chứng khoán chỉ cho thấy mức đền bù rủi ro trên thị trường tài chính. Bất kỳ một khoản đầu tư mới nào cũng đòi hỏi một mức doanh lợi dự kiến ít nhất là bằng mức đền bù của thị trường. Nếu không đạt đến mức đó thì người ta sẽ không đầu tư. Các nhà đầu tư chỉ thực sự có lợi nếu họ tìm được các khoản đầu tư mà mức doanh lợi dự kiến của chúng cao hơn mức đề nghị của thị trường, bởi vì những khoản đầu tư như vậy sẽ có giá trị hiện tại thuần tuý dương. Trên cơ sở nhận thức như vậy, nếu đặt câu hỏi: tỷ suất chiết khấu để xác định giá trị hiện tại là gì? thì câu trả lời sẽ là: Nên chọn doanh lợi dự kiến mà thị trường để nghị cho khoản đầu tư với cùng một múc rủi ro có hệ thống. Nói một cách khác, để xác định xem khoản đầu tư của ta có giá trị hiện tại dương hay không thì cần phải so sánh thu nhập dự kiến về khoản đầu tư mới và mức doanh lợi dự kiến mà thị trường đề nghị cho khoản đầu tư có cùng mức rủi ro có hệ thống (tức là có cùng hệ số ß).
Tỷ suất chiết khấu biểu thị bằng mức doanh lợi tôi thiêu cần đạt dược thường được gọi là chi phí của vốn cho một khoản đầu tư nhất định. Ở đây gọi là chi phí vốn bởi vì nêu đạt được mức doanh lợi tới thiểu này thì mối đạt đến điểm hoà vốn. Chi phí của vốn còn được coi như là chi phí cơ hội cho khoản đầu tư của doanh nghiệp.
Khi nói rằng khoản đầu tư mới có doanh lợi dự kiến lớn hơn mức doanh lợi mà thị trường đến bù cho khoản đầu tư có cùng mức độ rủi ro có hệ thống thì có nghĩa là đang sử dụng một cách có hiệu quả vốn đầu tư.
Nhằm giúp các bạn sinh viên có thêm tư liệu tham khảo, eLib đã tổng hợp nội dung bài giảng Bài 2: Doanh lợi, rủi ro và đường thị trường chứng khoán trên đây. Hy vọng tư liệu này giúp các bạn nắm bắt nội dung bài học dễ dàng hơn.
Tham khảo thêm
- doc Bài 1: Khái quát chung về doanh lợi và rủi ro




