Bài 1: Ứng dụng vào kinh tế - Kí hiệu, khái niệm, ví dụ
Nội dung bài giảng Bài 1: Ứng dụng vào kinh tế sau đây sẽ giúp các bạn tìm hiểu về Ký hiệu, các khái niệm cơ bản, bài toán cực đại, cực tiểu hóa, các ví dụ về kinh tế. Mời các bạn cùng tham khảo.
Mục lục nội dung

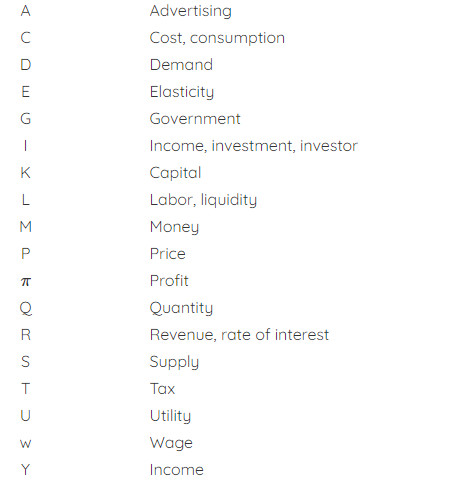
1. Ký hiệu
2. Các khái niệm cơ bản
Biên tế (biên) (marginal): Trong kinh tế, khái niệm biên tế dùng để chỉ sự thay đổi của một biến kinh tế này được gây ra bởi sự thay đổi của một biến kinh tế khác.Cho y = f(x) .và f là hàm khả vi, ta có biên tế của y tại x là \(My(x) = f'(x)\)
Ví dụ: Gọi x là lượng sản phẩm của một xí nghiệpt y là tổng chi phí sản xuất. Giả sử y phụ thuộc vào x như sau:
\(y=f(x)=ax^2+bx+c\) (a, b, c: hằng số dương)
Khi đó, ta có chi phí biên tế của xí nghiệp là: \(MC = f'(x) = 2ax + b\)
Chú ý: Khi \(y = f(x) = ax + b\) thì My = a. Như vậy, trong trường hợp hàm số là bậc nhất, giá trị biên tế chính là độ thay đổi của hàm số khi biến số tăng thêm 1 đơn vị.
Ví dụ: Giả sử tổng chi phí của một nhà máy tính theo công thức
\(C = WL+rK_o\)
Trong đó L chỉ số lượng lao động, W chỉ tiền lương cho mỗi lao động, Ko chỉ tiền vốn, r là lãi suất của vốn.
Ta có chi phí biên tế theo lao đông là: \(\frac{{\partial C}}{{\partial L}} = W\). Đây là chi phí tăng thêm khi thêm một lao động.
Độ co dãn (Elasticity): Trong nhiều ứng dụng kinh tế, tốc độ thay đổi của một hàm số thường phụ thuộc vào đơn vị tính của biến độc lập x và biến phụ thuộc y. Để tránh điều này, các nhà kinh tế sử dụng khái niệm độ co dãn. Độ co dãn của biến y theo biến x được định nghĩa như sau:
\({\varepsilon _{yx}}(x) = \frac{{dy/y}}{{dx/x}} = \frac{{dy}}{{dx}}.\frac{x}{y} = y'(x)\frac{x}{y}\)
Ví dụ: Tìm độ co dãn của y theo x, nếu:
a) \(y = {e^x};\varepsilon = y'(x).\frac{x}{y} = {e^x}.\frac{x}{y}\)
Khi x = 100 thì \(y=e^{100}\)
Khi x = 101 thì \(y=e^{101}\)
Ta có: \(\Delta y/y = \left( {{e^{101}} - {e^{100}}} \right)/{e^{100}} = e - 1 \approx 1,7 = 170\)
Mặt khác: \({e_{yx}}(100) = {e^{100}}.\frac{{100}}{{{e^{100}}}} = 100 \ne \Delta y/y\)
b) \(y = 3x + 5;\varepsilon = y'(x).\frac{x}{y} = \frac{{3x}}{{3x + 5}}\)
Khi x = 100 thì y =305
Khi x = 101 thì y = 308
Ta có \(\Delta y/y = (308 - 305)/305 = 3/305 = \frac{{300}}{{305}}\)
Mặt khác \(\varepsilon = 3.100/(3.100 + 5) = \frac{{300}}{{305}} = \Delta y/y\)
3. Bài toán cực đại, cực tiểu hóa
Hàm lồi, hàm lõi:
i) Tập lồi: Cho \(D \subset {R^n}\). D được gọi là tập lồi nếu \(\forall x,x' \in D,\forall \lambda \in (0,1) \Rightarrow \lambda x + (1 - \lambda )x' \in D\)
ii) Hàm số f gọi là lồi ngặt trên tập lồi \(D \subset {R^n}\) nếu \(f(\lambda x + (1 - \lambda )x') < \lambda f(x) + (1 - \lambda )f(x'),\forall x,x' \in D,\forall \lambda \in (0,1)\)
iii) Hàm số f gọi là lõm ngặt trên tập lồi \(D \subset {R^n}\) nếu \(f(\lambda x + (1 - \lambda )x') > \lambda f(x) + (1 - \lambda )f(x'),\forall x,x' \in D,\forall \lambda \in (0,1)\)
iv) Hàm số f gọi là lồi trên tập lồi \(D \subset {R^n}\) nếu \(f(\lambda x + (1 - \lambda )x') \le \lambda f(x) + (1 - \lambda )f(x'),\forall x,x' \in D,\forall \lambda \in (0,1)\)
v) Hàm số f gọi là lõm trên tập lồi \(D \subset {R^n}\) nếu \(f(\lambda x + (1 - \lambda )x') \ge \lambda f(x) + (1 - \lambda )f(x'),\forall x,x' \in D,\forall \lambda \in (0,1)\)
Cực trị địa phương, cực trị toàn cục của hàm số thực theo một biến số thực
Xét hàm số: \(y = f(x),x \in D \subset R\)
- Hàm số f gọi là đạt cực đại địa phương tại \(x_0 \in D\) nếu \(\exists \varepsilon > 0:\forall x \in \left( {{x_0} - \varepsilon ,{x_0} + \varepsilon } \right) \cap D\)ta có \(f(x) \le f({x_0})\)
- Hàm số f gọi là đạt cực đại địa phương tại \(x_0\) nếu \(\exists \varepsilon > 0:\forall x \in \left( {{x_0} - \varepsilon ,{x_0} + \varepsilon } \right) \cap D\)ta có \(f(x) \ge f({x_0})\)
- Hàm số f gọi là đạt cực đại địa phương tại \(x_0 \) nếu \(f(x) \le f({x_0}), \forall x \in D \) Hàm số f gọi là đạt cực đại địa phương tại \(x_0\) nếu \(f(x) \ge f({x_0}), \forall x \in D \)
Cực trị địa phương, cực trị toàn cục của hàm số thực theo hai biến số thực
Xét hàm số \(z=f(x,y)\) xác định trên \(D \subset {R^2}\)
Đặt \(B\left( {({x_0},{y_0}),\varepsilon } \right) = \left\{ {(x,y)/{{\left[ {{{(x - {x_0})}^2} + {{(y - {y_0})}^2}} \right]}^{\frac{1}{2}}} < \varepsilon } \right\},\varepsilon > 0\)
- Hàm số f gọi là đạt cực đại địa phương tại \((x_0,y_0) \in D\) nếu \(\exists \varepsilon > 0:\forall (x,y) \in B\left( {({x_0},{y_0}),\varepsilon } \right) \cap D\) ta có \(f(x,y) \le f({x_0},{y_0})\)
- Hàm số f gọi là đạt cực đại địa phương tại \((x_0,y_0) \) nếu \(\exists \varepsilon > 0:\forall (x,y) \in B\left( {({x_0},{y_0}),\varepsilon } \right) \cap D\) ta có \(f(x,y) \ge f({x_0},{y_0})\)
- Hàm số f gọi là đạt cực đại địa phương tại \((x_0,y_0) \in D\) nếu \(\forall (x,y) \in D,f(x,y) \le f({x_0},{y_0})\) Hàm số f gọi là đạt cực đại địa phương tại \((x_0,y_0) \in D\) nếu \(\forall (x,y) \in D,f(x,y) \ge f({x_0},{y_0})\)
Các chú ý ở trường hợp hàm một biến vẫn đúng cho trường hợp hai biến
Điều kiện của cực trị địa phương
Nhắc lại: Cho \(z=f(x,y)\) có các đạo hàm riêng cấp 2 liên tục, ta có vi phân cấp 1 và vi phân cấp 2 của f lần lượt như sau:
\(dz = f{'_x}dx + f{'_y}dy\)
\({d^2}z = f'{'_x}d{x^2} + 2f'{'_{xy}}dxdy + f'{'_{yy}}d{y^2}\)
Ta có: \({d^2}z = f'{'_{xx}}{\left[ {dx + \frac{{f'{'_{xy}}dy}}{{f'{'_{xx}}}}} \right]^2} + \left[ {\frac{{f'{'_{xx}}f'{'_{yy}} - f_{xy}^2}}{{f'{'_{xx}}}}} \right]d{y^2} \)
Suy ra:
- Nếu \({f'{'_{xx}}}<0\) và \({f'{'_{xx}}}{f'{'_{yy}}}-{f'{'_{xy}}}>0\) thì \(d^2z<0\) Nếu \({f'{'_{xx}}}>0\) và \({f'{'_{xx}}}{f'{'_{yy}}}-{f'{'_{xy}}}>0\) thì \(d^2z>0\)
Bây giờ, ta có điều kiện đủ của cực trị địa phương như sau:
- Nếu \(df({x_0},{y_0}) = 0\) và \({d^2}f({x_0},{y_0}) < 0\) thì f đạt cực đại địa phương tại \((x_0,y_0)\) Nếu \(df({x_0},{y_0}) = 0\) và \({d^2}f({x_0},{y_0}) > 0\) thì f đạt cực đại địa phương tại \((x_0,y_0)\)
Ta đặt :
\(H = \left[ {\begin{array}{*{20}{c}} {f'{'_{xx}}}&{f'{'_{xy}}}\\ {f'{'_{yx}}}&{f'{'_{yy}}} \end{array}} \right] \) (H gọi là ma trận Hesse)
\({H_1} = f'{'_{xx}},\,\,{H_2} = \left| H \right|\)
Ta có:
i) \({H_1} < 0,\,\,{H_2} > 0\) thì \(d^2f<0\) (cực đại địa phương)
ii) \({H_1} > 0,\,\,{H_2} > 0\) thì \(d^2f<0\) (cực tiểu địa phương)
+ Nếu \({d^2}z(x,y) > 0,\forall (x,y) \in D\)thì f lồi ngặt toàn cục trên D. Khi đó, một điểm cực tiểu địa phương cũng là cực tiểu toàn cục trên D.
+ Nếu \({d^2}z(x,y) < 0,\forall (x,y) \in D\)thì f lồi ngặt toàn cục trên D. Khi đó, một điểm cực tiểu địa phương cũng là cực đại toàn cục trên D.
Định lý: Cho \(z=f(x,y)\) có các đạo hàm riêng cấp 2 liên tục trên tập mở và lồi \(D \subset {R^2}\). Giả sử, tại \(({x_0},{y_0}) \in D\) ta có \(f{'_x}({x_0},{y_0}) = f{'_y}({x_0},{y_0}) = 0\)
Khi đó:
+ Nếu \({{\rm{H}}_1}{\rm{(x,y) > 0,}}{{\rm{H}}_2}{\rm{(x,y) > 0,}}\forall {\rm{(x,y)}} \in {\rm{D}}\)thì f đạt cực tiểu toàn cục trên D tại \((x_0,y_0)\)
+ Nếu \({{\rm{H}}_1}{\rm{(x,y) < 0,}}{{\rm{H}}_2}{\rm{(x,y) > 0,}}\forall {\rm{(x,y)}} \in {\rm{D}}\)thì f đạt cực đại toàn cục trên D tại \((x_0,y_0)\)
4. Các ví dụ về kinh tế
Ví dụ:
Giả sử hàm lợi nhuận của một xí nghiệp đối với một loại sản phẩm có dạng: \(\pi=R-C-T=PQ-cQ-tQ-f\)
trong đó \(\pi\) là lợi nhuận, R là doanh thu, c là chi phí gồm định phí f (độc lập với sản lượng) và biến phí cQ (c : biến phí đơn vị trên 1 sản phẩm, Q : sản lượng), t là thuế trên một đơn vị sản phẩm, T là tổng thuế.
Giả sử: \(P = a-bQ (a, b>0)\)
Khi đó, ta có: \(\pi=aQ-bQ^2-(c-t)Q-f\)
Để đơn giản, ta giả sử: \(a=10, b=1,c=2,f=1.\)Ta có: \(\pi=10Q-Q^2-(2+t)Q-1\)
Bài toán đạt ra là xí nghiệp muốn xác định mức sản lượng Q để lợi nhuận đạt cực đại. Đồng thời nhà nước cũng muốn xác định mức thuế t trên một đơn vị sản phẩm để tổng thuế T đạt cực đại.
Trước tiên, ta đứng trên cương vị của xí nghiệp, xem t như là tham số thì \(\pi\) là hàm số thực theo một biến số thực Q.
Điều kiện cần: \(\pi {'_Q} = - 2Q + 8 - t = 0 \Leftrightarrow Q = \frac{{8 - t}}{2}(0 < t < 8)\)
Điều kiện đủ: \(\pi '{'_{QQ}} = - 2 < 0,\forall Q\)
Vậy hàm \(\pi\) lõm ngặt toàn cục nên đạt cục đại toàn cục khi: \(Q = Q* = \frac{{8 - t}}{2}(0 < t < 8)\)
Với Q = Q*, ta có:
\(\begin{array}{l} T = tQ* = \frac{{8t - {t^2}}}{2}\\ \\ T{'_t} = \frac{{8 - t}}{2} = 0 \Leftrightarrow t = 4\\ \\ T'{'_{tt}} = - 1 < 0,\forall t \end{array} \)
Vậy hàm T lõm ngặt toàn cục nên đạt cực đại toàn cục khi: t = t* = 4 (thỏa điều kiện 0 < t < 8)
Khi đó, ta có: Q = Q * = 2
\(P = P^* = a - bQ^* = 10 - 2 = 8\) và \(\pi=\pi * = 20-4-6.2-1=3\)
Ví dụ: Giả sử hàm lợi nhuận của một công ty đối với một sản phẩm là: \(\Pi = R - C = PQ - wL - rK\)
trong đó \(\Pi\) là lợi nhuận, R là doanh thu, c là chi phí, L là lượng lao động, w là tiền lương của một lao động, K là tiền vốn, r là lãi suất của tiền vốn, p là đơn giá bán.
Giả sử Q là hàm sản xuất Cobb-Douglas dạng \(Q = {L^{1/3}}{K^{1/3}}\)
Giả sử w = 1, r = 0,02, P = 3
Khi đó, ta có: \(\Pi = 3{L^{1/3}}{K^{1/3}} - L - 0,02K\)
\(\Pi {'_L} = {L^{ - 2/3}}{K^{1/3}} - 1;\,\Pi {'_K} = {L^{1/3}}{K^{ - 2/3}} - 0,02\)
Ta có điều kiện cần để \(\Pi\) đạt cực trị tại (L, K) là:
\(\left\{ \begin{array}{l} \Pi {'_L} = {L^{ - 2/3}}{K^{1/3}} - 1 = 0\,\\ \Pi {'_K} = {L^{1/3}}{K^{ - 2/3}} - 0,02 = 0 \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} \frac{K}{{{L^2}}} = 1\\ \frac{L}{{{K^2}}} = {(0,02)^3} \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} K = {L^2}\\ L = {(0,02)^2}{K^2} = {(0,02)^3}{L^4} \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} K = 2500\\ L = 50 \end{array} \right. \)
Ta có ma trận Hesse:
\(H = \left[ {\begin{array}{*{20}{c}} {\Pi '{'_{LL}}}&{\Pi '{'_{LK}}}\\ {\Pi '{'_{KL}}}&{\Pi '{'_{KK}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} { - \frac{2}{3}{L^{ - 5/3}}{K^{1/3}}}&{\frac{1}{3}{L^{ - 2/3}}{K^{ - 2/3}}}\\ {\frac{1}{3}{L^{ - 2/3}}{K^{ - 2/3}}}&{ - \frac{2}{3}{L^{1/3}}{K^{ - 5/3}}} \end{array}} \right]\)
\(\begin{array}{l} {H_1} = - \frac{2}{3}{L^{ - 5/3}}{K^{1/3}} < 0\\ \\ {H_2} = \frac{4}{9}{L^{ - 4/3}}{K^{ - 4/3}} - \frac{1}{9}{L^{ - 4/3}}{K^{ - 4/3}} = \frac{1}{3}{L^{ - 4/3}}{K^{ - 4/3}} > 0\,\,\,(L,K > 0) \end{array} \)
Suy ra \(\Pi\) lõm ngặt toàn cục. Do đó, \(\Pi\) đạt cực đại toàn cục tại K = 2500, L = 50.
Ví dụ: Một công ty sản xuất độc quyền một loại sản phẩm và tiêu thụ 2 thị trường riêng biệt. Giả sử các hàm cầu trên 2 thị trường 1 và 2 lần lượt là \({Q_{{D_1}}} = 80 - \frac{{{P_1}}}{3},\,{Q_{{D_2}}} = 80 - \frac{{{P_2}}}{4}\), hàm tổng chi phí là: \(C({Q_1},{Q_2}) = {Q^2} + 30Q + 10\)
Trong đó Pi là đơn giá trên thị truon gừ thứ i, i = 1, 2; Q = Q1 + Q2 là tổng sản lượng. Tìm khối lượng sản phẩm công ty cung cấp cho các thị trường để lợi nhuận cao nhất?
Giải: Giả sử công ty cung cấp cho thị trường i là Qi. Ta có:
\({Q_1} = 80 - \frac{{{P_1}}}{3},{Q_2} = 80 - \frac{{{P_2}}}{4}\)và \(Q = Q_1 + Q_2\)
\(\begin{array}{l} \Rightarrow {P_1} = 240 - 3{Q_1},{P_2} = 320 - 4{Q_2}\\ \\ \Rightarrow {R_1} = (240 - 3{Q_1}){Q_1},\,{R_2} = (320 - 4{Q_2}){Q_2} \end{array} \)
Với Ri là doanh thu trên thị trường thứ i, i = 1, 2
Điều kiện cần để \(\pi=R_1+R_2-Q^2-30Q-10\)đạt cực trị là
\(\frac{{\partial \pi }}{{\partial {Q_1}}} = \frac{{\partial \pi }}{{\partial {Q_2}}} = 0 \Leftrightarrow \left\{ \begin{array}{l} 240 - 6{Q_1} = 30 + 2({Q_1} + {Q_2})\\ 320 - 8{Q_2} = 30 + 2({Q_1} + {Q_2}) \end{array} \right. \)
\( \Leftrightarrow \left\{ \begin{array}{l} 4{Q_1} + {Q_2} = 105\\ {Q_1} + 5{Q_2} = 145 \end{array} \right. \Leftrightarrow \left( {{Q_1},{Q_2}} \right) = (20,25) \)
Ta có:
\(\frac{{{\partial ^2}\pi }}{{\partial Q_1^2}} = - 8;\,\frac{{{\partial ^2}\pi }}{{\partial Q_2^2}} = - 10;\,\frac{{{\partial ^2}\pi }}{{\partial {Q_1}\partial {Q_2}}} = - 2\)
Đặt
\(\begin{array}{l} H = \left( {\begin{array}{*{20}{c}} { - 8}&{ - 2}\\ { - 2}&{ - 10} \end{array}} \right)\,\\ \\ {H_2} = \left| {\begin{array}{*{20}{c}} { - 8}&{ - 2}\\ { - 2}&{ - 10} \end{array}} \right| > 0,\,\,{H_1} = - 8 < 0,\,\forall ({Q_1},{Q_2}) \end{array} \)
⇒ \(\pi\) đạt cực đại toàn cục tại \(\left( {\overline {{Q_1}} ,\overline {{Q_2}} } \right) = (20,25)\)
Vậy công ty cung cấp cho:
- Thị trường thứ 1 là Q1 = 20 với đơn giá là P1 = 204 - 3Q1 = 180 Thị trường thứ 1 là Q2 = 25 với đơn giá là P2 = 320 - 4Q2 = 220
Ví dụ: Một xí nghiệp độc quyền sản xuất 2 loại sản phẩm. Biết hàm cầu của 2 loại sản phẩm lần lượt là \({Q_{D1}} = {\rm{ }}50{\rm{ }} - {\rm{ }}2{P_1}{\rm{ }} + {\rm{ }}{P_2},{\rm{ }}{Q_{D2}}{\rm{ }} = {\rm{ }}30{\rm{ }} + {\rm{ }}{P_1}{\rm{ }} - {\rm{ }}{P_2}\) và hàm tổng chi là \({\rm{C }} = {\rm{ }}2Q_1^2{\rm{ }} + {\rm{ }}{Q_1}{Q_2}{\rm{ }} + {\rm{ }}Q_2^2\) . Tìm mức sản lượng để lợi nhuận lớn nhất.
Giải
\(\left\{ \begin{array}{l} {Q_1} = {\rm{ }}50{\rm{ }} - {\rm{ }}2{P_1}{\rm{ }} + {\rm{ }}{P_2}{\rm{ }}\\ {Q_2}{\rm{ }} = {\rm{ }}30{\rm{ }} + {\rm{ }}{P_1}{\rm{ }} - {\rm{ }}{P_2} \end{array} \right. \Rightarrow \left\{ \begin{array}{l} {P_1} = 80 - {Q_1} - {Q_2}\\ {P_2} = 110 - {Q_1} - 2{Q_2} \end{array} \right. \)
Doanh thu \(R=P_1Q_1+P_2Q_2, \pi=R-C\)
\(\pi = (80 - {Q_1} - {Q_2}){Q_1} + (110 - {Q_1} - 2{Q_2}) - 2Q_1^2 + {Q_1}{Q_2} - Q_2^2\)
\(\left\{ \begin{array}{l} \frac{{\partial \pi }}{{\partial {Q_1}}} = - 6{Q_1} - 3{Q_2} + 80 = 0\\ \frac{{\partial \pi }}{{\partial {Q_2}}} = - 3{Q_1} - 6{Q_2} + 110 = 0 \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} 6{Q_1} + 3{Q_2} = 80\\ 3{Q_1} + 6{Q_2} = 110 \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} {Q_1} = \frac{{50}}{9}\\ {Q_2} = \frac{{140}}{9} \end{array} \right. \)
\(\frac{{{\partial ^2}\pi }}{{\partial {Q_1}}} = - 6\) và \(\frac{{{\partial ^2}\pi }}{{\partial {Q_2}}} = - 6\), \(\frac{{{\partial ^2}\pi }}{{\partial {Q_1}\partial {Q_2}}} = - 3\)
\({H_1} = 6 < 0,\,\,{H_2} = \left| {\begin{array}{*{20}{c}} { - 6}&{ - 3}\\ { - 3}&{ - 6} \end{array}} \right| = 27 > 0,\forall \left( {{Q_1},{Q_2}} \right) \)
\(\Rightarrow \pi\) đạt cực đại toàn cục tại \(\left( {{Q_1},{Q_2}} \right) = \left( {\frac{{50}}{9},\frac{{140}}{9}} \right) \)
Trên đây là nội dung bài giảng Bài 1: Ứng dụng vào kinh tế - Kí hiệu, khái niệm, ví dụ được eLib tổng hợp lại nhằm giúp các bạn sinh viên có thêm tư liệu tham khảo. Hy vọng đây sẽ là tư liệu giúp các bạn nắm bắt nội dung bài học dễ dàng hơn.
Tham khảo thêm
- doc Bài 2: Ứng dụng vào kinh tế - Cực trị ràng buộc



