Lý thuyết xác suất thống kê
Lý thuyết xác suất thống kê là môn học trang bị cho sinh viên các kiến thức về xác suất, môn học tập nghiên cứu các hiện tượng ngẫu nhiên và xử lý số liệu kinh tế - xã hội trong điều kiện bất định. Nhằm hỗ trợ cho quá trình học tập và ôn thi môn Lý thuyết xác suất thống kê, eLib giới thiệu đến bạn sinh viên chuyên ngành kinh tế chuyên mục Lý thuyết xác suất thống kê với các bài học, bài tập, bài luyện thi bám sát chương trình học trong giáo trình Xác suất thống kê. Hi vọng đây sẽ là những tư liệu hữu ích giúp bạn xây dựng phương hướng học tập và ôn tập hiệu quả chuẩn bị cho kì thi sắp tới. Mời các bạn cùng tham khảo.Mục lục nội dung
1. Lý thuyết xác suất thống kê là gì?
Lý thuyết xác suất thống kê là một bộ phận của toán học, nghiên cứu các hiện tượng ngẫu nhiên và ứng dụng chúng vào thực tế.
Lý thuyết xác suất cũng là cơ sở để nghiên cứu Thống kê môn học nghiên cứu các các phương pháp thu thập thông tin chọn mẫu, xử lý thông tin, nhằm rút ra các kết luận hoặc quyết định cần thiết. Ngày nay, với sự hỗ trợ tích cực của máy tính điện tử và công nghệ thông tin, lý thuyết xác suất thống kê ngày càng được ứng dụng rộng rãi và hiệu quả trong mọi lĩnh vực khoa học tự nhiên và xã hội. Chính vì vậy lý thuyết xác suất thống kê được giảng dạy cho hầu hết các nhóm ngành ở đại học.
2. Mục tiêu nghiên cứu môn Xác suất thống kê
Phần thứ nhất nghiên cứu việc xác lập tính quy luật của các hiện tượng ngẫu nhiên và xem xét các điều kiện để các quy luật đó được bộc lộ trên các hiện tượng cụ thể. Việc nắm bắt các quy luật này sẽ cho phép dự báo các hiện tượng ngẫu nhiên đó sẽ xảy ra như thế nào.
Phần thứ 2 nghiên cứu việc xây dựng các phương pháp thu thập và xử lý các số liệu thống kê nhằm rút ra các kết luận khoa học và thực tiễn.
3. Nội dung nghiên cứu môn Xác suất thống kê
Lý thuyết xác suất giới thiệu những nội dung cơ bản về biến cố ngẫu nhiên, xác suất; biến ngẫu nhiên và quy luật phân bố xác suất; các định lý giới hạn; vectơ ngẫu nhiên, kì vọng có điều kiện, hiệp phương sai và hệ số tương quan.
Thống kê toán bao gồm những nội dung cơ bản về lý thuyết mẫu, thống kê mô tả; các phương pháp ước lượng các tham số của biến ngẫu nhiên.
Chuyên đề Triết học Xác suất thống kê mà eLib tổng hợp dưới đây sẽ giới thiệu đến các bạn sinh viên bao gồm 3 phần:
4. Bài giảng Xác suất thống kê
Chương trình học môn Xác suất thống kê bao gồm 8 chương, nội dung giới thiệu cho người học các: khái niệm, quy luật, các đại lượng trong Xác suất. Mỗi chương gồm nội dung bài giảng chi tiết được tổng hợp và biên soạn từ cuốn giáo trình Xác suất thống kê do Bộ Giáo dục và Đào tạo ban hành. Cụ thể:
Chương 1: Xác suất của biến cố và công thức tính xác suất
Chương 2: Đại lượng ngẫu nhiên và phân phối xác suất
Chương 3: Một số quy luật phân phối xác suất thông dụng
Chương 4: Đại lượng ngẫu nhiên hai chiều - Hàm của các đại lượng ngẫu nhiên
Chương 5: Hàm của các đại lượng ngẫu nhiên và luật số lớn
Chương 6: Mẫu ngẫu nhiên
Chương 7: Ước lượng các số đặc trưng của tổng thể
Chương 8: Kiểm định giả thiết thống kê
5. Đề thi kết thúc môn Xác suất thống kê
Sau khi kết thúc nội dung bài học, để tiện cho các bạn sinh viên ôn tập, kiểm tra kiến thức, eLib đã tổng hợp bộ đề cương ôn tập môn Triết học, bộ trắc nghiệm ôn thi gồm những câu hỏi có gợi ý đáp án. Dưới đây là một số câu hỏi tự luận và trắc nghiệm mẫu.
5.1 Câu hỏi tự luận ôn tập Xác suất thống kê
Bài 1: Có 30 đề thi trong đó có 10 đề khó, 20 đề trung bình. Tìm xác suất để:
a. Một Học sinh bắt một đề gặp được đề trung bình.
b. Một Học sinh bắt hai đề, được ít nhất một đề trung bình.
Giải
a. Gọi A là biến cố Học sinh bắt được đề trung bình:
b. Gọi B là biến cố học sinh bắt được 1 đề trung bình và một đề khó
Gọi C là biến cố học sinh bắt được 2 đề trung bình.
Gọi D là biến cố học sinh bắt hai đề, được ít nhất một đề trung bình.
Khi đó:
Bài 2: Có hai lớp 10A và 10 B mỗi lớp có 45 học sinh, số học sinh giỏi văn và số học sinh giỏi toán được cho trong bảng sau. Có một đoàn thanh tra. Hiệu trưởng nên mời vào lớp nào để khả năng gặp được một em giỏi ít nhất một môn là cao nhất?
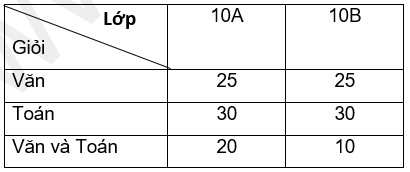
Giải
Gọi V là biến cố học sinh giỏi Văn, T là biến cố học sinh giỏi Toán.
Ta có: Lớp 10A
Lớp 10B:
Vậy nên chọn lớp 10B.
Bài 3: Lớp có 100 Sinh viên, trong đó có 50 SV giỏi Anh Văn, 45 SV giỏi Pháp Văn, 10 SV giỏi cả hai ngoại ngữ. Chọn ngẫu nhiên một sinh viên trong lớp. Tính xác suất:
a. Sinh viên này giỏi ít nhất một ngoại ngữ.
b. Sinh viên này không giỏi ngoại ngữ nào hết.
c. Sinh viên này chỉ giỏi đúng một ngoại ngữ.
d. Sinh viên này chỉ giỏi duy nhất môn Anh Văn.
Giải
a) Gọi A là biến cố Sinh viên giỏi Anh Văn.
Gọi B là biến cố Sinh viên giỏi Pháp Văn.
Gọi C là biến cố Sinh viên giỏi ít nhất một ngoại ngữ.
b) Gọi D là biến cố Sinh viên này không giỏi ngoại ngữ nào hết.
c)
d)
Bài 4: Trong một hộp có 12 bóng đèn, trong đó có 3 bóng hỏng. Lấy ngẫu nhiên không hoàn lại ba bóng để dùng. Tính xác suất để:
a. Cả ba bóng đều hỏng.
b. Cả ba bóng đều không hỏng?
c. Có ít nhất một bóng không hỏng?
d. Chỉ có bóng thứ hai hỏng?
Giải
Gọi F là biến cố mà xác suất cần tìm và Ai là biến cố bóng thứ i hỏng
a.
b.
c.
d.
5.2 Câu hỏi trắc nghiệm môn Xác suất thống kê
Câu 1. Tổ 1 có 5 sinh viên nữ và 6 sinh viên nam. Chọn ngẫu nhiên 1 sinh viên đi dự đại hội. Hỏi có bao nhiêu cách chọn?
A. 5
B. 6
C. 30
D. 11
Câu 2. Công thức tính số hoán vị của n phần tử là:
A. n!
B. (n-1)!
C. (n+1)!
D. n+2
Câu 3. Sắp xếp 5 sinh viên vào một bàn dài có 5 chỗ ngồi. Hỏi có bao nhiêu cách sắp xếp?
A. 60
B. 80
C. 100
D. 120
Câu 4. Hoán vị của n phần tử là:
A. Hoán đổi vị trí của n phần tử.
B. Sắp xếp n phần tử vào n vị trí.
C. Sắp xếp n phần tử vào n vị trí trên một vòng tròn
D. Sắp xếp n phần tử vào n vị trí theo hàng dọc hoặc hàng ngang
Câu 5. Hỏi có bao nhiêu cách xếp 1 hàng dọc cho 5 sinh viên nam và 3 sinh viên nữ sao cho sinh viên nam đứng gần nhau và sinh viên nữ đứng gần nhau?
A. 8!
B. 1440
C. 5!3!
D. Số khác
Câu 6. Đội văn nghệ của lớp có 4 nữ và 6 nam. Hỏi có bao nhiêu cách chọn 1 đôi hát song ca nam - nữ?
A. 10!
B. 4!6!
C. 24
D. 45
Câu 7. Từ các số 2, 3, 4, 5, 6. Có thể lập được bao nhiêu số tự nhiên có 3 chữ số đôi một khác nhau?
A. 60
B. 10
C. 6
D. Số khác
Câu 8. Có bao nhiêu số tự nhiên có 3 chữ số đôi một khác nhau ?
A. 720
B. 648
C. 640
D. 900
6. Tài liệu tham khảo môn Xác suất thống kê
Trên đây là một số thông tin về môn Lý thuyết xác suất thống kê mà eLib muốn chia sẻ đến các bạn sinh viên. Ngoài ra, eLib còn tổng hợp các dạng bài tập khác nhau, giáo trình môn Xác suất thống kê, cuốn sách nhập môn Xác suất thống kêhay nhất hay những bài giảng chi tiết môn Xác suất thống kê. Chúc các bạn ôn tập và học tập thật tốt.
Để củng cố kiến thức và nắm vững nội dung bài học mời các bạn cùng làm Bộ câu hỏi trắc nghiệm môn Lý thuyết xác suất thống kê có đáp án dưới đây.
Tham khảo thêm
- Bài 1: Phép thử và các loại biến cố
- Bài 2: Mối quan hệ giữa các biến cố
- Bài 3: Xác suất của biến cố và các tính xác suất (phần 1)
- Bài 3: Xác suất của biến cố và cách tính xác suất (phần 2)
- Bài 4: Công thức cộng xác suất
- Bài 5: Công thức nhân xác suất
- Bài 6: Công thức Bernoulli
- Bài 7: Công thức xác suất đầy đủ và Bayes
- Bài 1: Định nghĩa, phân loại và phân phối xác suất của đại lượng ngẫu nhiên
- Bài 2: Các tham số đặc trưng của đại lượng ngẫu nhiên (phần 1)




