Toán 8 Ôn tập Chương 2: Đa Giác. Diện Tích Đa Giác

Định nghĩa:

Chú ý:

- Đa giác $n$ đỉnh $\left( {n \ge 3} \right)$  được gọi là hình $n$ giác hay hình $n$-cạnh.

- Tổng các góc của đa giác $n$ cạnh bằng $\left( {n - 2} \right).180^\circ$ .

- Mỗi góc của đa giác đều $n$ cạnh bằng $\dfrac{{\left( {n - 2} \right).180^\circ }}{n}$.

- Số các đường chéo của đa giác lồi $n$ cạnh bằng $\dfrac{{n\left( {n - 3} \right)}}{2}$  .

Diện tích hình thang

Diện tích hình thang bằng nửa tích của tổng hai đáy với chiều cao: $S = \dfrac{{\left( {a + b} \right)h}}{2}$

Diện tích hình bình hành

Diện tích hình bình hành bằng tích một cạnh với chiều cao ứng với cạnh đó: $S = a.h$ .

Diện tích tứ giác có hai đường chéo vuông góc

Diện tích tứ giác có hai đường chéo vuông góc bằng nửa tích hai đường chéo

Diện tích hình thoi

Diện tích hình thoi bằng nửa tích hai đường chéo: $S = \dfrac{1}{2}{d_1}.{d_2}$

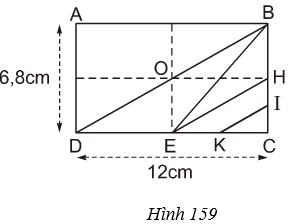
Cho hình chữ nhật ABCD. Gọi H, I, E, K lần lượt là các trung điểm của BC, HC, DC, EC (h.159). Tính

a) Diện tích tam giác DBE

b) Diện tích tứ giác EHIK

Hướng dẫn giải

a) Ta có: $DE = \dfrac{1}{2}DC = \dfrac{1}{2}.12 = 6\left( {cm} \right)$ (tính chất trung điểm)

${S_{DBE}} = \dfrac{1}{2}.DE.BC = \dfrac{1}{2}.6.6,8$$\, = 20,4$ $\left( {c{m^2}} \right)$

b) Ta có :  $HC = \dfrac{1}{2}BC = \dfrac{1}{2}.6,8 = 3,4\,\left( {cm} \right)$ (tính chất trung điểm)

 $HI = \dfrac{1}{2}HC = \dfrac{1}{2}.3,4 = 1,7\left( {cm} \right)$ (tính chất trung điểm)

$EC = DE = 6cm$ (tính chất trung điểm)

$EK = KC = \dfrac{1}{2}EC = \dfrac{1}{2}.6 = 3\,\left( {cm} \right)$ (tính chất trung điểm)

Do đó

${S_{EHIK}} = {S_{EHK}} + {S_{HKI}}$

$= \dfrac{1}{2}EK.HC + \dfrac{1}{2}HI.KC$

$= \dfrac{1}{2}EK.HC + \dfrac{1}{2}EK.HI$

$= \dfrac{1}{2}EK\left( {HC + HI} \right)$

${S_{EHIK}} = \dfrac{1}{2}.3.\left( {3,4 + 1,7} \right)$$\,= \dfrac{1}{2}.3.5,1 = 7,65\,(c{m^2})$

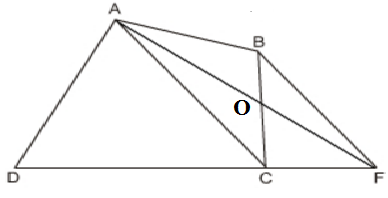
Trên hình 160 (AC // BF), hãy tìm tam giác có diện tích bằng diện tích tứ giác ABCD.

Hướng dẫn giải

Gọi $O$ là giao điểm của $AF$ và $BC$.

Ta có $\Delta A{\rm{D}}F$ có diện tích bằng diện tích tứ giác $ABCD$.

Thật vậy, do $AC// BF$ nên  ${S_{ABC}} = {S_{AFC}}$ vì có cùng đáy $AC$ và cùng chiều cao là khoảng cách giữa hai đường thẳng song song $AC, BF.$

Ta có:  ${S_{ABC}} = {S_{AFC}}$ (chứng minh trên)

$\Rightarrow {S_{ABO}} + {S_{ACO}} = {S_{CF{\rm{O}}}} + {S_{AC{\rm{O}}}}$

$\Rightarrow {S_{ABO}} = {S_{CFO}}$.

Do đó  ${S_{ADF}} = {S_{AOCD}} + {S_{CFO}}$$= {S_{AOCD}} + {S_{ABO}}= {S_{ABCD}}$

Vậy  ${S_{ADF}} = {S_{ABCD}}$

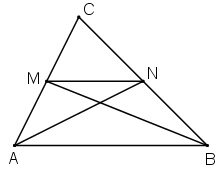
Cho tam giác $ABC.$ Gọi $M, N$ là các trung điểm tương ứng của $AC, BC.$ Chứng minh rằng diện tích của hình thang $ABNM$ bằng $\dfrac{3}{4}$ diện tích của tam giác $ABC.$

Hướng dẫn giải

Vẽ hai trung tuyến $AN, BM$ của $∆ABC.$ Ta có:

 ${S_{MNA}} =\dfrac{1}{2}{S_{ACN}}$

(có cùng đường cao từ đỉnh $N$, đáy  $AM = \dfrac{1}{2}AC)$

 ${S_{ACN}} =\dfrac{1}{2}{S_{ABC}}$

(có cùng đường cao từ đỉnh $A$, đáy  $CN = \dfrac{1}{2}BC)$

 ${S_{ABN}} =\dfrac{1}{2}{S_{ABC}}$

(có cùng đường cao từ đỉnh $A$, đáy  $BN = \dfrac{1}{2}BC)$

Suy ra  ${S_{AMN}}= \dfrac{1}{2}{S_{ACN}} =\dfrac{1}{2}.\dfrac{1}{2}{S_{ABC}}$$=\dfrac{1}{4}{S_{ABC}}$

Vậy  ${S_{ABN}} + {S_{AMN}} = \dfrac{1}{2}{S_{ABC}} +\dfrac{1}{4}{S_{ABC}}$$=\dfrac{3}{4}S_{ABC}$

Tức là  ${S_{ABNM}} = \dfrac{3}{4}{S_{ABC}}$

Câu 1: Cho tam giác $ABC$ với ba đường cao $AA’,\, BB’,\ CC’.$ Gọi $H$ là trực tâm của tam giác đó.

Chứng minh rằng: \(\eqalign{{HA'} 

Câu 2: Cho tam giác $ABC$

a) Tính tỉ số các đường cao $BB’$ và $CC’$ xuất phát từ các đỉnh $B$ và $C$

b) Tại sao nếu $AB < AC$ thì $BB’ < CC’ ?$

Câu 3: Qua tâm $O$ của hình vuông $ABCD$ cạnh $a,$ kẻ đường thẳng $l$ cắt cạnh $AB$ và $CD$ lần lượt tại $M$ và $N.$ Biết $MN = b.$ Hãy tính tổng các khoảng cách từ các đỉnh của hình vuông đến đường thẳng $l$ theo $a$ và $b$ ($a$ và $b$ có cùng đơn vị đo)

Câu 4: Tam giác $ABC$ có hai trung tuyến $AM$ và $BN$ vuông góc với nhau. Hãy tính diện tích tam giác đó theo $AM$ và $BN$

Câu 5: Cho hình bình hành $ABCD.$ Gọi $K$ và $L$ là hai điểm thuộc cạnh $BC$ sao cho $BK = KL = LC.$ Tính tỉ số diện tích của :

a) Các tam giác $DAC$ và $DCK$

b) Tam giác $DAC$ và tứ giác $ADLB$

c) Các tứ giác $ABKD$ và $ABLD$

Câu 1: Một đa giác lồi 10 cạnh thì có số đường chéo là:

A. 35                                     

B. 30                                       

C. 70                                       

D. 27

Câu 2: Cho đa giác cạnh, số đường chéo của đa giác đó là:

A. 36

B. 27

C. 20

D. 18

Câu 3: Cho hình chữ nhật ABCD có AD = 8cm, AB = 9cm. Các điểm M, N trên đường chéo BD sao cho BM = MN = ND. Tính diện tích tam giác CMN.

A. 12 $cm^{2}$

B. 24 $cm^{2}$

C. 36 $cm^{2}$

D. 6 $cm^{2}$

Câu 4: Một hình thang có đáy nhỏ là 9 cm , chiều cao là 4 cm , diện tích là 50 $cm^{2}$. Đáy lớn là: 

A. 25 cm                           

B. 18 cm                          

C. 16 cm                         

D. 15 cm

Câu 5: Hình thoi có độ dài hai đường chéo là 15 cm và 20 cm. Tính độ dài đường cao của hình thoi.

A. 12 cm

B. 7, 5 cm

C. 15 cm

D. 24 cm

Qua bài học này, các em nắm được một số nội dung chính như sau:

• Nắm vững công thức tính diện tích các đa giác đơn giản, đặc biệt là các cách tính diện tích tam giác và hình thang
• Biết chia một cách hợp lý đa giác cần tìm diện tích thành những đa giác đơn giản mà có thể tính được diện tích
• Biết thực hiện các phép vẽ và đo cần thiết .