Giải bài tập SGK Toán 9 Bài: Luyện tập

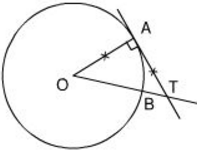
Xem hình 7. Tính số đo của góc ở tâm AOB và số đo cung lớn AB.

Phương pháp giải

- Tam giác vuông có hai cạnh góc vuông bằng nhau là tam giác vuông cân. 

- Tam giác vuông cân có hai góc nhọn bằng \(45^o\)

Hướng dẫn giải

Tam giác AOT có: \(\widehat A=90^o; AO=AT\)

Suy ra, tam giác AOT vuông cân tại A

 \(\Rightarrow\widehat{AOB}=\widehat{ATO}=45^o\)

Vậy số đo cung nhỏ AB bằng số đo góc \(\widehat{AOB}\) bằng \(45^o\)

Do vậy số đo cung lớn AB bằng \(360^o-45^o=315^o\)

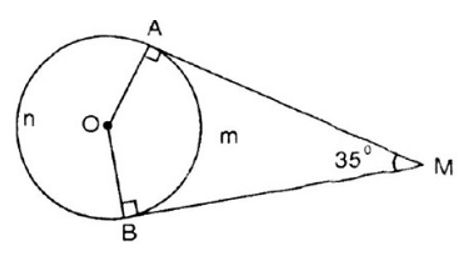
Hai tiếp tuyến của đường tròn (O) tại A và B cắt nhau tại M. Biết góc \(AMB = 35^o\).

a) Tính số đo của góc ở tâm tạo bởi bán kính OA, OB.

b) Tính số đo mỗi cung AB (cung lớn và cung nhỏ).

Phương pháp giải

a) Theo định lý tổng bốn góc trong một tứ giác ta có:

\(\widehat{OAM}+\widehat{OBM}+\widehat{AOB}+\widehat M=360^o\),  từ đó suy ra \(\widehat{AOB}\)

b) Sử dụng:

Số đo cung nhỏ bằng số đo góc ở tâm chắn cung đó

Số đo cung lớn bằng \(360^\circ \) trừ số đo cung nhỏ (có chung hai mút với cung lớn).

Hướng dẫn giải

a) Xét tứ giác AOBM:

Vì AM và BM là các tiếp tuyến nên ta có: \(\widehat{OAM}=\widehat{OBM}=90^o\)

Theo định lý tổng bốn góc trong một tứ giác ta có:

\(\widehat{OAM}+\widehat{OBM}+\widehat{AOB}+\widehat M=360^o\\\Rightarrow 90^o+90^o+\widehat{AOB}+35^o=360^o\\ \Rightarrow \widehat{AOB}=180^o-35^o=145^o\)

b) Gọi cung nhỏ AB là \(\overset\frown{{AmB}} \) và cung lớn AB là \( \overset\frown{{AnB}} \)

Ta có: \(sđ \overset\frown{{AmB}}=\widehat{AOB}=145^o \)

Suy ra \(\text{sđ} \overset\frown{{AnB}}=360^o- \text{sđ} \overset\frown{{AmB}}=360^o-145^o=215^o\)

Cho tam giác đều ABC. Gọi O là tâm của đường tròn đi qua ba đỉnh A, B, C.

a) Tính số đo các góc ở tâm tạo bởi hai trong ba bán kính OA, OB, OC.

b) Tính số đo các cung tạo bởi hai trong ba điểm A, B, C.

Phương pháp giải

a) Ta có góc ở tâm tạo bởi hai trong ba bán kính OA, OB và OC là góc \(\widehat{AOB}\), \(\widehat{AOC}\), \(\widehat{BOC}\).

Chứng minh: 

\(\Delta ABO=\Delta CAO=\Delta BCO\) (g.c.g)

Vậy \(\widehat{AOB}=\widehat{AOC}=\widehat{BOC}\)

b) Chỉ ra  \(\text{sđ}\overset\frown{{AB}} =\text{sđ}\overset\frown{{AC}}=\text{sđ}\overset\frown{{BC}}=120^o\)

Từ đó, ta có:

+) \(\text{sđ}\overset\frown{{ACB}}=360^o-\text{sđ}\overset\frown{{AB}}\)

+) \(\text{sđ}\overset\frown{{ABC}}=360^o-\text{sđ}\overset\frown{{AC}}\)

+) \(\text{sđ}\overset\frown{{BAC}}=360^o-\text{sđ}\overset\frown{{BC}}\)

Hướng dẫn giải

a) Góc ở tâm tạo bởi hai trong ba bán kính OA, OB và OC là góc \(\widehat{AOB}\), \(\widehat{AOC}\), \(\widehat{BOC}\).

Vì ABC là tam giác đều nên O là giao điểm ba đường trung trực đồng thời là giao điểm của ba đường phân giác.

Suy ra \(\widehat{ABO}=\widehat{BAO}=\widehat{ACO}=\widehat{CAO}=\widehat{CBO}=\widehat{BCO}=\dfrac{60^o}{2}=30^o\)

Xét ba tam giác AOB, AOC và BOC có 

+) \(AB=AC=BC\)

+) \(\widehat{BAO}=\widehat{ACO}=\widehat{CBO}=30^o\)

+) \(\widehat{ABO}=\widehat{CAO}=\widehat{BCO}=30^o\)

Suy ra \(\Delta ABO=\Delta CAO=\Delta BCO\) (g.c.g)

Vậy \(\widehat{AOB}=\widehat{AOC}=\widehat{BOC}=180^o-30^o.2=120^o\)

b) Các điểm A, B, C chia đường tròn O thành 3 cung nhỏ \(\overset\frown{{AB}},\overset\frown{{BC}}, \overset\frown{{CA}}\) có số đo lần lượt bằng số đo các góc ở tâm  \(\widehat{AOB}\), \(\widehat{AOC}\), \(\widehat{BOC}\).

Suy ra: \(\text{sđ}\overset\frown{{AB}} =\text{sđ}\overset\frown{{AC}}=\text{sđ}\overset\frown{{BC}}=120^o\)

Từ đó, ta có:

+) \(\text{sđ}\overset\frown{{ACB}}=360^o-\text{sđ}\overset\frown{{AB}}=240^o\)

+) \(\text{sđ}\overset\frown{{ABC}}=360^o-\text{sđ}\overset\frown{{AC}}=240^o\)

+) \(\text{sđ}\overset\frown{{BAC}}=360^o-\text{sđ}\overset\frown{{BC}}=240^o\)

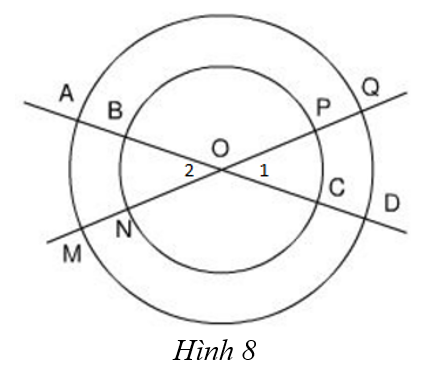
Cho hai đường tròn cùng tâm O với bán kính khác nhau. Hai đường thẳng đi qua O cắt hai đường tròn đó tại các điểm A, B, C, D, M, N, P, Q (hình 8).

a) Em có nhận xét gì về số đo của các cung nhỏ AM, CP, BN, DQ?

b) Hãy nêu tên các cung nhỏ bằng nhau.

c) Hãy nêu tên hai cung lớn bằng nhau.

Phương pháp giải

Số đo của cung nhỏ bằng số đo của góc ở tâm chắn cung đó.

Số đo của cung lớn bằng hiệu giữa \({360^o}\) và số đo của cung nhỏ (có chung hai mút với cung lớn)

Hai cung bằng nhau có số đo bằng nhau.

Hướng dẫn giải

a) Ta có:

 \(sđ\overset\frown{{AM}}=\widehat{AOM};\\ sđ\overset\frown{{BN}}=\widehat{BON}\)

mà \(\widehat{AOM}=\widehat{BON}\) nên \(sđ\overset\frown{{AM}}=sđ\overset\frown{{BN}}\)

Tương tự, ta cũng chứng minh được: \(sđ\overset\frown{{PC}}=sđ\overset\frown{{QP}}\,\,(=\widehat{QOD})\)

b) Hai cung nhỏ bằng nhau:

- Trên đường tròn \((O;OB)\) có:

+) \(sđ\overset\frown{{BN}}=sđ\overset\frown{{PC}}\Rightarrow \overset\frown{{BN}}=\overset\frown{{PC}} \)

+) \(sđ\overset\frown{{BP}}=sđ\overset\frown{{NC}}\Rightarrow \overset\frown{{BP}}=\overset\frown{{NC}} \)

- Trên đường tròn \((O;OA)\) có:

+) \(sđ\overset\frown{{AM}}=sđ\overset\frown{{QD}}\Rightarrow\overset\frown{{AM}}=\overset\frown{{QD}}\)

+) \(sđ\overset\frown{{QA}}=sđ\overset\frown{{MD}}\Rightarrow\overset\frown{{QA}}=\overset\frown{{MD}}\)

c) Hai cung lớn bằng nhau:

- Trên đường tròn \((O;OB)\) có:

+) \(sđ\overset\frown{{BN}}+sđ\overset\frown{{BP}}+sđ\overset\frown{{PC}}=sđ\overset\frown{{BN}}+sđ\overset\frown{{NC}}+sđ\overset\frown{{PC}}\\ \Rightarrow\overset\frown{{NBC}}=\overset\frown{{BNP}}\)

- Trên đường tròn \((O;OA)\) có:

+) \(sđ\overset\frown{{AM}}+sđ\overset\frown{{AQ}}+sđ\overset\frown{{QD}}=sđ\overset\frown{{AM}}+sđ\overset\frown{{MD}}+sđ\overset\frown{{QD}}\\ \Rightarrow\overset\frown{{MAD}}=\overset\frown{{AMQ}}\)

Mỗi khẳng định sau đây đúng hay sai? Vì sao?

a) Hai cung bằng nhau thì có số đo bằng nhau

b) Hai cung có số đo bằng nhau thì bằng nhau.

c) Trong hai cung, cung nào có số đo lớn hơn là cung lớn hơn.

d) Trong hai cung trên một đường tròn, cung nào có số đo nhỏ hơn thì nhỏ hơn.

Phương pháp giải

So sánh hai cung:

Ta chỉ so sánh hai cung trong một đường tròn hay trong hai đường tròn bẳng nhau: Khi đó:

- Hai cung được gọi là bằng nhau nếu chúng có số đo bằng nhau.

- Trong hai cung, cung nào có số đo lớn hơn được gọi là cung lớn hơn.

Hướng dẫn giải

a) Đúng

Chú ý: Khi ta nói hai cung bằng nhau, nghĩa là hai cung này so sánh được (tức chúng cùng nằm trong một đường tròn hoặc trong hai đường tròn bằng nhau). Do đó, theo cách so sánh hai cung đã biết thì hai cung bằng nhau thì số đo bằng nhau. 

b) Sai. Không rõ hai cung nằm trên một đường tròn hay trên hai đường tròn bằng nhau không.

c) Sai. Không rõ hai cung nằm trên một đường tròn hay trên hai đường tròn bằng nhau không.

d) Đúng

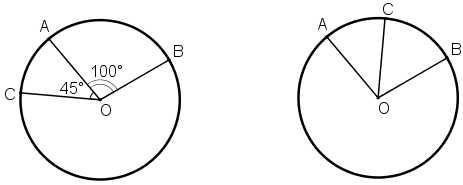
Trên đường tròn tâm O lấy ba điểm A, B, C sao cho \(\widehat{AOB} = 100^o\),  \(sđ\overset\frown{AC} = 45^o\). Tính số đo của cung nhỏ BC và cung lớn BC. (Xét cả hai trường hợp: điểm C nằm trên cung nhỏ AB, điểm C nằm trên cung lớn AB).

Phương pháp giải

Trên đường tròn (O), nếu điểm C nằm giữa hai điểm A và B thì \(\text{sđ}\overset\frown{AB}=\text{sđ}\overset\frown{AC}+\text{sđ}\overset\frown{BC} \)

Hướng dẫn giải

TH1: Điểm C thuộc cung nhỏ AB.

Vì C thuộc cung nhỏ AB nên ta có:

\(\begin{align} & \text{sđ}\overset\frown{AB}=\text{sđ}\overset\frown{AC}+\text{sđ}\overset\frown{BC} \\ & \Rightarrow {{100}^{o}}={{45}^{o}}+\text{sđ}\overset\frown{BC} \\ & \Rightarrow \text{sđ}\overset\frown{BC}={{100}^{o}}-{{45}^{o}}={{55}^{o}} \\ \end{align}\)

Số đo cung lớn BC là \(360^o-55^o=305^o\)

TH2: Điểm C thuộc cung lớn AB.

Suy ra A thuộc cung nhỏ BC.

Ta có: 

\(\begin{align} & \text{sđ}\overset\frown{BC}=\text{sđ}\overset\frown{AB}+\text{sđ}\overset\frown{AC} \\ & \Rightarrow \text{sđ}\overset\frown{BC}={{100}^{o}}+{{45}^{o}}={{145}^{o}} \\ \end{align}\)

Số đo cung lớn BC là \(360^o-145^o=215^o\)