Giải bài tập SGK Vật lý 12 nâng cao Bài 47: Mẫu nguyên tử Bo và quang phổ vạch của nguyên tử Hiđrô

Trạng thái dừng của một nguyên tử là

A. trạng thái đứng yên của nguyên tử.

B. trạng thái chuyển động đều của nguyên tử.

C. trạng thái trong đó mọi êlectron của nguyên tử đều không chuyển động đối với hạt nhân.

D. một trong số các trạng thái có năng lượng xác định, mà nguyên tử có thể tồn tại.

Phương pháp giải

Để trả lời câu hỏi này cần nắm được định nghĩa về trạng thái dừng của nguyên tử

Hướng dẫn giải

- Trạng thái dừng của một nguyên tử là một trong số các trạng thái có năng lượng xác định mà nguyên tử có thể tồn tại.

- Chọn đáp án D.

Ở trạng thái dừng, nguyên tử

A. không bức xạ và không hấp thụ năng lượng.

B. không bức xa, nhưng có thể hấp thụ năng lượng.

C. không hấp thụ, nhưng có thể bức xạ năng lượng.

D. vẫn có thể hấp thụ và bức xạ năng lượng.

Phương pháp giải

Nguyên tử khi ở trạng thái dừng không bức xạ và cũng không hấp thụ năng lượng

Hướng dẫn giải

- Ở trạng thái dừng nguyên tử không bức xạ và không hấp thụ năng lượng.

- Chọn đáp án A.

Dãy Ban-me ứng với sự chuyển êlectron từ quỹ đạo ở xa hạt nhân về quỹ đạo nào sau đây?

A. Quỹ đạo K.                                     B. Quỹ đạo L.

C. Quỹ đạo M.                                    D. Quỹ đạo N.

Phương pháp giải

Đối với sự phát xạ của nguyên tử Bo, các bức xạ dịch chuyển về quỹ đạo dừng L tạo thành dãy Ban - me

Hướng dẫn giải

- Dãy Ban-me ứng với sự dịch chuyển các quỹ đạo dừng bên ngoài về quỹ đạo L.

- Chọn đáp án B.

Bước sóng của vạch quang phổ thứ nhất trong dãy Lai-man là λ₀=122 nm, của hai vạch H_α,H_β lần lượt là λ₁=0,656μm và λ₂=0,486μm. Hãy tính bước sóng hai vạch tiếp theo trong dãy Lai-man và vạch đầu tiên trong dãy Pa-sen.

Phương pháp giải

Áp dụng công thức tiên đề Bo:

\({\varepsilon _{21}} = {E_2} - {E_1}\)

và công thức: \(\varepsilon = \frac{{hc}}{\lambda }\)

để tính lần lượt các bước sóng theo công thức sau:

a)  \(\frac{{hc}}{{{\lambda _{MK}}}} = \frac{{hc}}{{{\lambda _{ML}}}} + \frac{{hc}}{{{\lambda _{LK}}}} \Rightarrow {\lambda _{MK}}\) ;

\(\frac{{hc}}{{{\lambda _{NK}}}} = \frac{{hc}}{{{\lambda _{NL}}}} + \frac{{hc}}{{{\lambda _{LK}}}} \Rightarrow {\lambda _{NK}}\)

để tính bước sóng hai vạch tiếp theo trong dãy Lai-man

b) \(\frac{{hc}}{{{\lambda _{NM}}}} = \frac{{hc}}{{{\lambda _{NK}}}} + \frac{{hc}}{{{\lambda _{MK}}}} \Rightarrow {\lambda _{NM}}\)

để tính bước sóng vạch đầu tiên trong dãy Pa-sen

Hướng dẫn giải

- Để giải bài toán nguyên tử Hidrô, ta lưu ý sử dụng tốt sơ đồ chuyển mức năng lượng như sau:

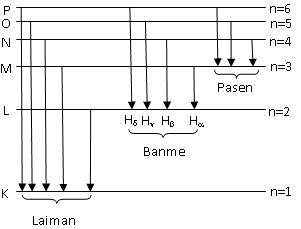
Theo giả thiết: 

+ Vạch thứ nhất trong dãy Lai-man là λ₀=λ_LK=122(nm)

+ Vạch thứ nhất và vạch thứ hai trong dãy Ban-me là:

λ₁=λ_ML=0,656(μm) và λ₂=λ_NL=0,486(μm)

a) Bước sóng của hai vạch tiếp theo trong dãy Lai-man là: λ_MK và λ_NK

Theo tiên đề Bo:           

\(\begin{array}{l} {\varepsilon _{MK}} = {E_M} - {E_K}\\ = {E_M} - {E_L} + {E_L} - {E_K}\\ \Rightarrow {\varepsilon _{MK}} = {\varepsilon _{ML}} + {\varepsilon _{LK}}\\ \Leftrightarrow \frac{{hc}}{{{\lambda _{MK}}}} = \frac{{hc}}{{{\lambda _{ML}}}} + \frac{{hc}}{{{\lambda _{LK}}}}\\ \Leftrightarrow \frac{1}{{{\lambda _{MK}}}} = \frac{1}{{{\lambda _{ML}}}} + \frac{1}{{{\lambda _{LK}}}} = \frac{1}{{0,656}} + \frac{1}{{0,122}}\\ \Rightarrow {\lambda _{MK}} = 0,1029(\mu m) \end{array}\)                                                             

Tương tự :                  

\(\begin{array}{l} {\varepsilon _{NK}} = {E_N} - {E_K}\\ = {E_N} - {E_L} + {E_L} - {E_K} = {\varepsilon _{NL}} + {\varepsilon _{LK}}\\ \Leftrightarrow \frac{1}{{{\lambda _{NK}}}} = \frac{1}{{{\lambda _{NL}}}} + \frac{1}{{{\lambda _{LK}}}} = \frac{1}{{0,486}} + \frac{1}{{0,122}}\\ \Rightarrow {\lambda _{NK}} = 0,0975\left( {\mu m} \right) \end{array}\)                               

b) Bước sóng của vạch đầu tiên trong dãy Pasen: λ_NM

Ta có :

\(\begin{array}{l} {\varepsilon _{NM}} = {E_N} - {E_M}\\ = \left( {{E_N} - {E_K}} \right) - \left( {{E_M} - {E_K}} \right) = {\varepsilon _{NK}} - {\varepsilon _{MK}}\\ \Rightarrow \frac{1}{{{\lambda _{NM}}}} = \frac{1}{{{\lambda _{NK}}}} - \frac{1}{{{\lambda _{MK}}}} = \frac{1}{{0,0975}} - \frac{1}{{0,1029}}\\ \Rightarrow {\lambda _{NM}} = 1,858(\mu m) \end{array}\)