Giải bài tập SGK Vật lý 12 nâng cao Bài 21: Dao động điện từ

Trong bảng phân tích dao động theo từng thời điểm trên Hình 21.3, ta có:

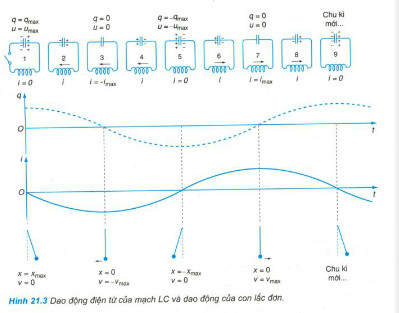
A. Năng lượng điện trường cực đại tại thời điểm số 2.

B. Năng lượng từ trường cực đại tại thời điểm số 4.

C. Năng lượng điện trường cực đại tại thời điểm số 6.

D. Năng lượng từ trường cực đại tại thời điểm số 7.

Phương pháp giải

- Vận dụng biểu thức tính năng lượng từ trường: 

W_t=1/2Li²

- Vận dụng biểu thức tính năng lượng điện trường: 

W_d=1/2Cu²

Hướng dẫn giải

- Ta có:

+ Năng lượng từ trường: Wt=1/2Li²

=> Năng lượng từ trường cực đại khi i=i_max

+ Năng lượng điện trường: W_d=1/2Cu²

=> Năng lượng điện trường cực đại khi u=u_max

- Ta suy ra:

+ Năng lượng từ trường cực đại tại thời điểm số 3 và số 7 vì lúc này i=i_max

\(\Rightarrow {W_{L\max }} = \frac{1}{2}Li_{\max }^2.\)

+ Năng lượng điện trường cực đại tại thời điểm số 1 và số 5 vì lúc này u=u_max

=> Chọn đáp án D

Dao động điện từ trong mạch dao động dao động LC là quá trình

A. Biến đổi không tuần hoàn của điện tích trên tụ điện.

B. Biến đổi theo hàm mũ của cường độ dòng điện.

C. Chuyển hoá tuần hoàn giữa năng lượng từ trường và năng lượng điện trường.

D. Bảo toàn hiệu điện thế giữa hai cực tụ điện.

Phương pháp giải

Để trả lời câu hỏi này cần nắm được lý thuyết dao động điện từ

Hướng dẫn giải

A, B, D - sai vì: điện tích, dòng điện và điện áp biến thiên điều hòa theo quy luật dạng sin

C - đúng: Dao động điện từ trong mạch dao động LC là quá trình chuyển hoá tuần hoàn giữa năng lượng từ trường và năng lượng điện trường.

⇒ Chọn đáp án C.

Trong một mạch dao động LC, tụ điện có điện dung là 5μF cường độ tức thời của dòng điện là i=0,05sin2000t(A).Tìm độ tự cảm và biểu thức cho điện tích của tụ. 

Phương pháp giải

- Tính tần số góc theo công thức: ω=1√LC

- Cường độ dòng điện được tính theo công thức: I₀=ωq₀

- Vận dụng tính chất: điện tích trên bản tụ chậm pha so với dòng điện một góc π/2 để tìm pha ban đầu

Hướng dẫn giải

- Mạch dao động có C=5(μF)

- Dòng điện có biểu thức: i=0,05sin2000t

Với:

\(\begin{array}{l} \omega = 2000(rad/s)\\ \Rightarrow {q_0} = \frac{{{I_0}}}{\omega } = \frac{{0,05}}{{2000}} = {2,5.10^{ - 5}}(C) \end{array}\)

- Ta có:

\(\begin{array}{l} \omega = \frac{1}{{\sqrt {LC} }} \Rightarrow {\omega ^2} = \frac{1}{{LC}}\\ \Rightarrow L = \frac{1}{{{\omega ^2}C}} = \frac{1}{{{{(2000)}^2}{{.5.10}^{ - 6}}}} \Rightarrow L = 0,05(H). \end{array}\)

- Điện tích của tụ có biểu thức: (Vì q chậm pha so với ii một góc π/2)

\(\begin{array}{l} q = {q_0}\sin (2000t - \frac{\pi }{2})\\ \Rightarrow q = {2,5.10^{ - 5}}\sin (2000t - \frac{\pi }{2})(C) \end{array}\)

Một mạch dao động LC có năng lượng là 36.10⁻⁶J và điện dung của tụ điện C là 2,5μF. Tìm năng lượng tập trung tại cuộn cảm khi hiệu điện thế giữa hai bản cực của tụ điện là 3 V. 

Phương pháp giải

- Tính năng lượng điện từ theo công thức: W=W_L+W_C

- Công thức tăng lượng điện trường: W_C=Cu²/2

- Tính năng lượng từ trường theo công thức: W_L=Li²/2

Hướng dẫn giải

- Mạch dao động có năng lượng điện từ W=36.10⁻⁶J

- Tụ điện C=2,5(μF) có hiệu điện thế giữa hai cực của bản tụ là U=3 (V)

- Năng lượng điện trường tập trung tại tụ điện là:

\(\begin{array}{l} {W_C} = \frac{{C{U^2}}}{2}\\ = \frac{{{{2,5.10}^{ - 6}}{{.3}^2}}}{2} = {1,125.10^{ - 5}}(J)\\ = {11,25.10^{ - 6}}(J) \end{array}\)

- Năng lượng từ trường tập trung tại cuộn cảm là:

\(\begin{array}{l} {W_L} = W - {W_C}\\ = {36.10^{ - 6}} - {11,25.10^{ - 6}}\\ = {24,75.10^{ - 6}}(J). \end{array}\)