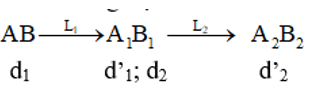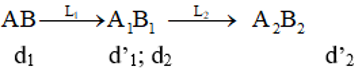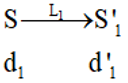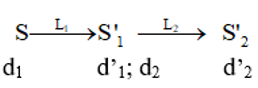Giải bài tập SGK Vật lý 11 Bài 30: Giải bài toán về hệ thấu kính

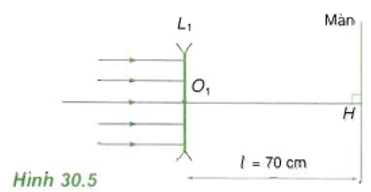
Một học sinh bố trí thí nghiệm theo sơ đồ hình 30.5. Thấu kính phân kỳ L₁ có tiêu cự là f₁ = -10cm Khoảng cách từ ảnh S’₁ tạo bởi L₁ đến màn có giá trị nào?

A. 60cm

B. 80cm

C. Một giá trị khác A,B

D. Không xác định được, vì không có vật nên L₁ không tạo được ảnh.

Phương pháp giải

- Chùm tia tới là chùm song song

⇒ d = ∞ ⇒ d' = f₁ = -10cm < 0

- Áp dụng công thức:

S₁H = S₁O + OH = |d'| + l để tính khoảng cách từ ảnh đến màn

Hướng dẫn giải

- Chùm tia tới là chùm song song:

⇒ d = ∞ ⇒ d' = f₁ = -10cm < 0

- S’₁ là ảnh ảo nằm tại tiêu điểm ảnh F’, trước thấu kính và cách thấu kính 10cm

- Khoảng cách từ ảnh S’₁ tạo bởi L₁ đến màn:

S₁H = S₁O + OH = |d'| + l = 10 + 70 = 80cm

- Chọn đáp án B.

Tiếp theo các giả thiết cho ở bài tập 1.

Đặt giữa L₁ và H một thấu kính hội tụ L₂. Khi xê dịch L₂ học sinh này nhận thấy chỉ có một vị trí duy nhất của L₂ tạo được điểm sáng tại H. Tiêu cự của (L₂) là bao nhiêu?

A. 10cm

B. 15cm

C. 20cm

D. Một giá trị khác A,B,C.

Phương pháp giải

- Dựa vào sơ đồ tạo ảnh, ta có:

+  d1 = ∞ ⇒ d'₁ = f₁ = -10 cm

+ d'₂ = d₂ = 40 cm

- Áp dụng công thức:

\(f = \frac{{{d_2}.d{'_2}}}{{{d_{}} + d{'_2}}}\) để tính tiêu cự của L₂

Hướng dẫn giải

- Sơ đồ tạo ảnh của hệ hai thấu kính đồng trục:

- Trong đó: d₁ = ∞

⇒ d'₁ = f₁ = -10 cm

⇒ d₂ + d'₂ = 70 – (-10) = 80 cm

- Điều kiện để chỉ có một vị trí duy nhất của (O₂) tạo được điểm sáng tại H là:

d'₂ = d₂ và d₂ + d'₂ = S₁H = 80 cm

- Khoảng cách d'2 là:

d'₂ = d₂ = 40 cm

- Tiêu cự của L₂ là:

 \(f = \frac{{{d_2}.d{'_2}}}{{{d_{}} + d{'_2}}} = 20cm\)

- Chọn đáp án C.

Hai thấu kính, một hội tụ (f₁ =20 cm), một phân kỳ (f₂ = -10cm), có cùng trục chính. Khoảng cách hai quang tâm là l = 30cm. Vật AB vuông góc với trục chính được đặt bên trái (L₁ )và cách (L₁ ) một đoạn d₁.

a) Cho d₁ = 20cm, hãy xác định vị trí và tính số phóng đại ảnh cuối cùng cho bởi hệ hai thấu kính. Vẽ ảnh.

b) Tìm d₁ để ảnh sau cùng là ảnh ảo và bằng hai lần vật.

Phương pháp giải

- Áp dụng các quy tắc vẽ đường truyền của tia sáng để vẽ ảnh:

+ Tia đi qua quang tâm O thì truyền thẳng

+ Tia tới đi qua tiêu điểm F của thấu kính thì tia ló song song với trục ∆

+ Tia tới song song với trục ∆ thì tia ló đi qua tiêu điểm F’

- Áp dụng công thức:

k = A’B’/AB = d'₁d'₂/d₁d₂ để tính độ phóng đại

- Áp dụng công thức:

\(d{'_1} = \frac{{{d_1}.{f_1}}}{{{d_1} - {f_1}}}\) để tính d’₁

- Giải phương trình và nhận nghiệm d₁ = 35cm

Hướng dẫn giải

a) Vẽ ảnh:

- Sơ đồ tạo ảnh của hệ hai thấu kính đồng trục:

- Ta có: d₁ = 20cm; f₁ = 20cm; l = 30cm 

- Khoảng cách d’₁ là:

 \(d{'_1} = \frac{{{f_1}.{d_1}}}{{{d_1} - {f_1}}} = \infty \)

- Khoảng cách d’₂ là:

d₂ = l - d'₁ = -∞ ⇒ d'₂ = f₂ = -10cm

- Độ phóng đại là: 

\(k = \frac{{{d'_1}.{d'_2}}}{{{d_1}.{d_2}}} = \frac{{d{'_2}}}{{{d_1}}}.\frac{{d{'_1}}}{{l - d{'_1}}} = \frac{{d{'_2}}}{{{d_1}}}.\frac{1}{{\frac{l}{{d{'_1}}} - 1}} = 0,5\)

b) Ảnh A’₂B’₂ là ảnh ảo và bằng hai lần vật:

- Độ phóng đại là:

 \(k = \frac{{A{'_2}B{'_2}}}{{AB}} = \frac{{A{'_2}{O_2}}}{{A{O_1}}} = \frac{{\left| {{d_2}} \right|}}{{{d_1}}} = \frac{{\left| { - 10} \right|}}{{20}} = \frac{1}{2}\)

- Khoảng cách d’₁ là:

 \(d{'_1} = \frac{{{d_1}.{f_1}}}{{{d_1} - {f_1}}} = 20.\frac{{{d_1}}}{{{d_1} - 20}}\)

- Khoảng cách d₂ là: 

\(\begin{array}{l} {d_2} = 1 - {d_1}\\ \Rightarrow {d_2} = 30 = 20.\frac{{{d_1}}}{{{d_1} - 20}} = \frac{{10({d_1} - 60)}}{{{d_1} - 20}} \end{array}\)

- Ta có:

 \(\frac{{5.(60 - {d_1})}}{{{d_1} - 40}} < 0 \Rightarrow {d_1} < 40cm;{d_1} > 60cm\)

- Giải phương trình ta được:

+ d₁ = 35cm (thỏa mãn)

+ d₁ = 45 cm (không thỏa mãn)

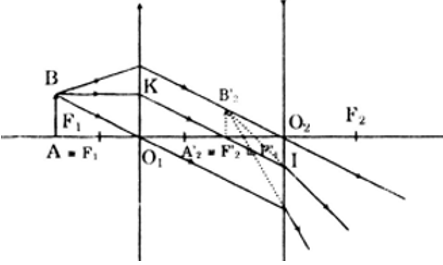
Một hệ bao gồm hai thấu kính (L1 )và (L₂) đồng trục có tiêu điểm ảnh chính của (L₁) trùng với tiểu điểm chính của (L₂). Chiếu một chùm tia sáng song song tới (L₁) theo bất kì.

a) Chứng minh chùm tia ló ra khỏi (L₂) cũng là chùm tia ló song song.

b) Vẽ đường đi của chùm tia sáng ứng với các trườn hợp:

- (L₁) và (L₂) đều là thấu kính hội tụ.

- (L₁) là thấu kính hội tụ; (L₂) là thấu kính phân kì.

- (L₁) là thấu kính phân kì; (L₂) là thấu kính hội tụ.

Phương pháp giải

- Áp dụng công thức:

l = O₁O₂ = f₁ + f₂     

- d'₂ = ∞ ⇒ chùm tia ló ra khỏi (L₂) là song song

- Áp dụng các quy tắc vẽ đường truyền của tia sáng để vẽ ảnh:

+ Tia đi qua quang tâm O thì truyền thẳng

+ Tia tới đi qua tiêu điểm F của thấu kính thì tia ló song song với trục ∆

+ Tia tới song song với trục ∆ thì tia ló đi qua tiêu điểm F’

Hướng dẫn giải

a) Chứng minh:

Sơ đồ tạo ảnh của hệ hai thấu kính đồng trục:

- Hệ gồm hai thấu kính L₁ và L₂ đồng trục có tiêu điểm ảnh chính của (L₁) trùng với tiêu điểm vật chính của L₂

⇒ l = O₁O₂ = f₁ + f₂

- Chùm tia sáng tới song song:

d₁ = ∞ ⇒ d'₁ = f₁

- Khoảng cách d₂ là:

  d₂ = l - d'₁ = f₂ ⇒ d'₂ = ∞

⇒ chùm tia ló ra khỏi (L₂) là chùm tia song song.

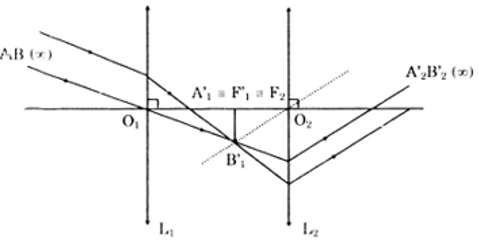
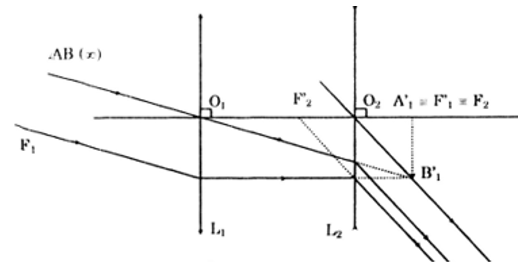
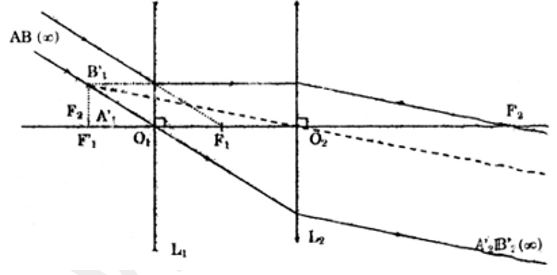
b) Vẽ đường đi của chùm tia sáng ứng với các trường hợp:

- (L₁) và (L₂) đều là thấu kính hội tụ: 

- L₁ là thấu kính hội tụ; L₂ là thấu kính phân kì:

- L₁ là thấu kính phân kì; L₂ là thấu kính hội tụ:

Một thấu kính mỏng phẳng – lồi L₁ có tiêu cự f₁ = 60 cm được ghép sát đồng trục với một thâu kính mỏng phẳng – lồi khác L₂ có tiêu cự f₂ = 30 cm. Mặt phẳng có hai thấu kính sát nhau.

Thấu kính (L₁) có đường kình rìa gấp đôi đường kính rìa của thấu kính (L₂ ). Một điểm sáng S nằm trên trục chính của hệ, trước( L₁)

a) Chứng tỏ có hai ảnh của S được tạo bởi hệ.

b) Tìm điều kiện về vị trí của S để hai ảnh đều thật và hai ảnh đều ảo.

Phương pháp giải

a) Chứng minh

- Áp dụng các công thức:

+  \(\frac{1}{{{d_1}}} + \frac{1}{{d{'_1}}} = \frac{1}{{{f_1}}}\)

+ \(\frac{1}{{{d_1}}} + \frac{1}{{d{'_2}}} = \frac{1}{{{f_{12}}}}\)

+ D₁₂ = D₁ + D₂

+ Suy ra f₁ ≠ f₁₂ 

⇒ Hai hình ảnh S’₁ và S’₂ không trùng nhau

⇒ Luôn tồn tại hai ảnh.

b) Tìm điều kiện

- Điều kiện để hai ảnh S’₁ và S’₂ đều thật:

d₁ > f₁ 

- Điều kiện để hai ảnh S’₁ và S’₂ đều ảo:

d₁ > f₁₂ 

Hướng dẫn giải

a) Chứng minh

- Khi chùm tia sáng từ S tới các điểm tới từ miền vành ngoài của thấu kính L₂ trở ra

⇒ Chỉ đi qua thấu kính L₁ và chùm tia ló sẽ tạo ảnh S₁

- Chùm tia sáng từ S tới các điểm tới trong trong khoảng từ tâm thấu kính tới miền vành của thấu kính L₂ 

⇒ Đi qua cả hai thấu kính L₁ và L₂ và chùm tia ló sẽ tạo ảnh S’₂

- Như vậy sẽ có hai ảnh đồng thời được tạo thành như hình vẽ:

+ Sơ đồ tạo ảnh qua thấu kính L₁:

+ Sơ đồ tạo ảnh của hệ hai thấu kính đồng trục:

- Trong đó:

+ \(\frac{1}{{{d_1}}} + \frac{1}{{d{'_1}}} = \frac{1}{{{f_1}}}\)

+ \(\frac{1}{{{d_1}}} + \frac{1}{{d{'_2}}} = \frac{1}{{{f_{12}}}}\)

+ D₁₂ = D₁ + D₂

- Vì f₁ ≠ f₁₂ ⇒ d'₁ ≠ d'₂ 

⇒ Hai hình ảnh S’₁ và S’₂ không trùng nhau

⇒ Luôn tồn tại hai ảnh.

b) Tìm điều kiện

Vì f₁ > f₁₂ nên:

- Điều kiện để hai ảnh S’₁ và S’₂ đều thật là:

d₁ > f₁ = 60cm

- Điều kiện để hai ảnh S’1 và S’2 đều ảo:

d₁ > f₁₂ = 20cm