Giải bài tập SGK Vật lý 11 Bài 27: Phản xạ toàn phần

Thế nào là phản xạ toàn phần? Nêu điều kiện để phản xạ toàn phần.

Phương pháp giải

- Phản xạ toàn phần: tia sáng chỉ bị phản xạ mà không bị khúc xạ tại mặt phân cách giữa hai môi trường

- Điều kiện xảy ra: Góc tới i lớn hơn hoặc bằng góc giới hạn

Hướng dẫn giải

Định nghĩa:

Hiện tượng ánh sáng truyền từ môi trường có chiết suất lớn đến mặt giới hạn với môi trường có chiết suất nhỏ hơn, chỉ bị phản xạ mà không bị khúc xạ gọi là hiện tượng phản xạ toàn phần.

Điều kiện phản xạ toàn phần:

- Ánh sáng truyền từ môi trường chiết quang hơn sang môi trường chiết quang kém

- Góc tới i phải lớn hơn hoặc bằng góc giới hạn

- Góc giới hạn:

sin_igh = n₂/n₁, với n₂ < n₁

- Nếu ánh sáng đi từ môi trường có chiết suất n ra không khí thì:

sin_igh = 1/n

So sánh phản xạ toàn phần với phản xạ thông thường.

Phương pháp giải

So sánh về cường độ sáng, điều kiện xảy ra và nguyên tắc truyền tia sáng của hai loại phản xạ.

Hướng dẫn giải

Giống nhau:

- Tia phản xạ đều truyền ngược lại được môi trường đầu

- Đều tuân theo định luật phản xạ

Khác nhau:

- Cường độ của tia phản xạ toàn phần lớn bằng cường độ tia tới; Còn cường độ của tia sáng phản xạ thông thường nhỏ hơn cường độ tia tới

- Điều kiện xảy ra:

+ Tia phản xạ thông thường xảy ra khi gặp mặt phẳng nhẵn dưới mọi góc

+ Phản xạ toàn phần chỉ xảy ra khi tia sáng đi từ môi trường chiết quang hơn sang môi trường chiết quang kém và góc tới i > i_gh.

Cáp quang là gì? Cấu tạo của cáp quang. Nêu một vài ứng dụng.

Phương pháp giải

- Cáp quang là bó sợ quang

- Cấu tạo: gồm phần lõi và phần vỏ

- Ứng dụng: truyền tín hiệu, y học, ...

Hướng dẫn giải

- Cáp quang là bó sợ quang. Mỗi sợi là một dây trong suốt có tính dẫn sáng nhờ phản xạ toàn phần

- Cấu tạo: gồm 2 phần

+ Phần lõi trong suốt, bằng thủy tinh có chiết suất lớn n₁

+ Phần võ cũng trong suốt, bằng thủy tinh có chiết suất n₂ nhỏ hơn phần lõi

- Phản xạ toàn phần xảy ra ở mặt phân cách giữa lõi và vỏ làm cho ánh sáng truyền đi theo sợi quang

- Ứng dụng:

+ Truyền tín hiệu thông tin trong việc liên lạc

+ Nội soi trong y học.

Giải thích tại sao kim cương và pha lên sáng lóng lánh? Người ta tạo ra nhiều mặt kim cương hay các vật pha lê để làm gì?

Phương pháp giải

Để trả lời câu hỏi này cần nắm được định nghĩa hiện tượng phản xạ toàn phần và các ứng dụng của nó.

Hướng dẫn giải

- Kim cương và pha lê sáng lóng lánh vì nó có thể phản xạ toàn phần ánh sáng mặt trời chiếu vào nó.

- Người ta tạo ra nhiều mặt cho kim cương hay các vậy bằng pha lê để làm cho chùm tia tới có nhiều khả năng phản xạ toàn phần dưới các góc tới khác nhau ứng với các mặt khác nhau, làm cho kim cương và pha lê lóng lánh hơn.

Một chùm tia sáng hẹp truyền từ môi trường (1) chiết suất n₁ tới mặt phẳng phân cách với môi trường (2) chiết suất n₂. Cho biết n₁ < n₂ và i có giá trị thay đổi.

Trường hợp nào sau đây có hiện tượng phản xạ toàn phần?

A. Chùm tia sáng gần như sát mặt phẳng phân cách

B. Góc tới i thỏa mãn điều kiện sini > n₁/n₂ 

C. Góc tói i thỏa mãn điều kiện sini < n₁/n₂ 

D. Không trường hợp nào đã nêu

Phương pháp giải

- Điều kiện phản xạ toàn phần tại là: 

\(i \ge {i_{gh}} \Rightarrow \sin i \ge \sin {i_{gh}} = \frac{{{n_2}}}{{{n_1}}}\)

- Suy ra n₁ > n₂

Hướng dẫn giải

- Điều kiện có phản xạ toàn phần là n₁ > n₂

- Chọn đáp án D.

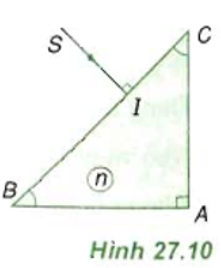
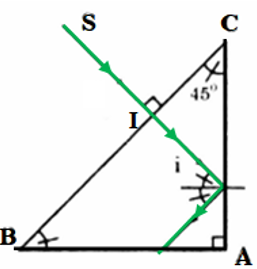
Một chùm tia sáng hẹp SI truyền trong mặt phẳng tiết diện vuông góc của khối trong suốt như hình 27.1. Tia sáng phản xạ toàn phần ở mặt AC. Trong điều kiện đó, chiết n của khối trong suốt có giá trị như thế nào?

A. n ≥ √2

B. n < √2

C. 1 < n < √2

D. Không xác định được.

Phương pháp giải

- Tia SI truyền thẳng vào môi trường trong suốt ABC

- Không bị khúc xạ

⇒ sini = sin45^o = 1/√2

- Áp dụng công thức:

sin_igh = 1/n để  tính chiết suất n

Hướng dẫn giải

- ΔABC vuông cân tại A

⇒ ∠B = ∠C = 45^o

- Ta có: SI ⊥BC

⇒ Tia SI truyền thẳng mà không bị khúc xạ

- Góc tới i ở mặt AC là:

i = ∠B = ∠C = 45^o 

- Sin góc i là: 

sini = sin45^o = 1/√2

- Tia sáng phản xạ toàn phần ở mặt AC

⇒ i ≥ i_gh 

- Chiết suất là:

sini ≥ sin_igh = 1/n ⇒ n ≥ √2

- Chọn đáp án A.

Có ba môi trường trong suốt với cùng góc tới:

- Nếu tia sáng truyền từ (1) vào (2) thì góc khúc xạ là 30^o.

- Nếu tia sáng truyền từ (1) vào (3) thì góc khúc xạ là 45^o.

Góc giới hạn toàn phần ở mặt phân cách (2) và (3) có giá trị như thế nào ( tính tròn số)?

A. 30^o

B. 42^o

C. 45^o

D. Không xác định được.

Phương pháp giải

- Áp dụng định luật khúc xạ cho cả hai môi trường

- Rút ra tỉ số: 

⇒ Môi trường (2) chiết quang hơn môi trường (3)

- Áp dụng công thức:

sini_gh23 = n₃/n₂ để  tính góc giới hạn

Hướng dẫn giải

- Khi truyền từ môi trường từ (1) vào môi trường (2)

n₁.sini = n₂sinr12 (∗)

- Khi truyền từ môi trường từ (1) vào môi trường (3)

n₁.sini = n₃.sinr₁₃ (∗∗)

- Trong đó: r₁₂ = 30^o; r₁₃ = 45^o

- Từ (∗) và (∗∗) suy ra:

n₂sinr₁₂ = n₃sinr₁₃ 

⇒ Môi trường (2) chiết quang hơn môi trường (3)

- Góc giới hạn phản xạ toàn phần ở mặt phân cách (2) và (3) được tính khi truyền từ môi trường (2) vào môi trường (3)

- Chọn đáp án C.

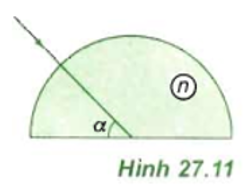
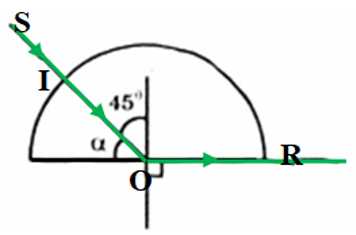
Một khối bán trụ trong suốt có chiết suất n = 1,41 ≈ √2. Một chùm tia sáng hẹp nằm trong mặt phẳng của tiết diện vuông góc, chiếu tới khối bám trụ như hình 27.11. Xác định đường đi của chùm tia với các giá trí sau đây của góc α.

A. α = 60^o

B. α = 45^o

C. α = 30^o

Phương pháp giải

- Tìm góc tới: i = 90^o – α

- Áp dụng công thức:

sin_igh = 1/n để  tính góc giới hạn

- Áp dụng định luật khúc xạ ch từng trường hợp

a) r = 45^o

b) r = 90^o 

c) Không có tia khúc xạ

Hướng dẫn giải

- Tia sáng tới có đường kéo dài qua O

- Tia tới SI vuông góc mặt phẳng trụ: i = 0

⇒ Tia sáng sẽ truyền thẳng vào khối trong suốt tới O

- Tia sáng SO tạo với pháp tuyến ON của mặt phân cách phẳng một góc tới i

- Ta có: i = 90^o - α

- Góc giới hạn khi ánh sáng truyền từ khối bán trụ ra không khí:

\(\sin {i_{gh}} = \frac{1}{n} = \frac{1}{{\sqrt 2 }} \Rightarrow {i_{gh}} = {45^o}\)

a) α = 60^o

- Góc tới là: i = 90^o – α = 30^o ⇒ i < i_gh

- Áp dụng định luật khúc xạ: 

\({\mathop{\rm s}\nolimits} {\rm{inr}} = n.\sin i = \sqrt 2 \sin {30^o} = \frac{{\sqrt 2 }}{2}\)

- Góc khúc xạ là: r = 45^o 

⇒ Tia khúc xạ hợp với pháp tuyến của mặt phẳng phân cách của khối bán trụ góc khúc xạ 45^o 

- Hình vẽ:

b) α = 45^o

- Góc tới là: i = 90^o – α = 45^o ⇒ i = i_gh

- Góc khúc xạ là: r = 90^o

- Tia khúc xạ đi sát mặt phân cách của khối tròn

- Hình vẽ:

c) α = 30^o

- Góc tới là:  i = 90^o – α = 60^o ⇒ i > i_gh

- Xảy ra phản xạ toàn phần

⇒ Không có tia khúc xạ ra ngoài không khí.

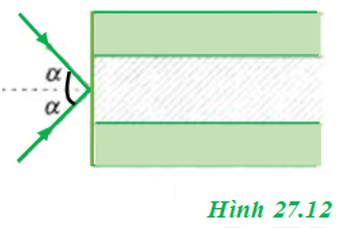
Một sợi quang hình trụ lõi có chiết suất n₁ = 1,50. Phần vỏ bõ cõ chiết suất n₂ = 1,41 ≈ √2. Chùm tia tới hội tụ ở mặt trước của sợi với góc tới 2α như hình 27.12. Xác định α để các tia sáng của các tia sáng của chùm truyền đi được trong ống.

Phương pháp giải

- Điều kiện phản xạ toàn phần tại J là:

 \({i_1} \ge {i_{gh}} \Rightarrow \sin {i_1} \ge \sin {i_{gh}} = \frac{{{n_2}}}{{{n_1}}}\)

- Áp dụng định luật khúc xạ:

\(\sin \alpha = {n_1}.{\mathop{\rm s}\nolimits} {\rm{inr}}\) để tìm góc tới

- Rút ra được góc tới \(\alpha \le {30^o}\) thì thỏa điều kiện

Hướng dẫn giải

- Mọi tia sáng trong chùm đều thỏa mãn điều kiện phản xạ toàn phần.

- Điều kiện phản xạ toàn phần tại J là:

\({i_1} \ge {i_{gh}} \Rightarrow \sin {i_1} \ge \sin {i_{gh}} = \frac{{{n_2}}}{{{n_1}}}\)

- Góc khúc xạ là: 

\(r = {90^o} - {i_1} \Rightarrow \cos r = \sin {i_1} \ge \frac{{{n_2}}}{{{n_1}}}\)

- Áp dụng định luật khúc xạ tại mặt trước của ống quang ta được:

\(\sin \alpha = {n_1}.{\mathop{\rm s}\nolimits} {\rm{inr}} = {n_1}\sqrt {1 - {{\cos }^2}r} \le {n_1}\sqrt {1 - {{\left( {\frac{{{n_2}}}{{{n_1}}}} \right)}^2}} \)

- Góc tới là:

 \(\sin \alpha \le 1,5.\sqrt {1 - {{\left( {\frac{{\sqrt 2 }}{{1,5}}} \right)}^2}} = 0,5 \Rightarrow \alpha \le {30^o}\)