Giải bài tập SGK Toán 6 Bài 15: Phân tích một số ra thừa số nguyên tố

 Phân tích các số sau ra thừa số nguyên tố
a) \(60\)                      b) \(84\);                    c) \(285\);
d) \(1035\);                 e) \(400\);                  g) \(1000000\).

Phương pháp giải

Phân tích một số tự nhiên lớn hơn 1 ra thừa số nguyên tố là viết số đó dưới dạng một tích các thừa số nguyên tố.

Hướng dẫn giải

Câu a

\(60 = 2^2 . 3 . 5\)

Câu b

\(64 = 2^6\)

Câu c

\(285 = 3 . 5 . 19\)

Câu d

\(1035 = 3^2 . 5 . 23\)

Câu e

\(400 = 2^4 . 5^2\)

Câu f

\(1000000 = 2^6 . 5^6\)

An phân tích các số \(120, 306, 567\) ra thừa số nguyên tố như sau

\(120 = 2 . 3 . 4 . 5\)

\(306 = 2 . 3 . 51\)

\(567 = 9^2. 7\)

An làm như trên có đúng không ? Hãy sửa lại trong trường hợp An làm không đúng.

Phương pháp giải

Phân tích một số tự nhiên lớn hơn 1 ra thừa số nguyên tố là viết số đó dưới dạng một tích các thừa số nguyên tố.

Số nguyên tố là số tự nhiên lớn hơn 1 chỉ có 2 ước là 1 và chính nó.

Hướng dẫn giải

An làm không đúng vì chưa phân tích hết ra thừa số nguyên tố. Chẳng hạn: \(4, 51, 9\) không phải là các số nguyên tố

Ta phải phân tích lại như sau

\(120 = 2.3.4.5 = 2.3.(2.2).5= {2^3}.3.5\)   

\(306 = 2.3.51 = 2.3.(3.17) = {2.3^2}.17\)

\(567 = 81.7 = 9.9.7 = 3^2.3^2.7 = 3^4. 7\)

Phân tích các số sau ra thừa số nguyên tố rồi cho biết mỗi số đó chia hết cho các số nguyên tố nào ?

a) \(225\);                    b) \(1800\);                     

c) \(1050\);                  d) \(3060\).

Phương pháp giải

Phân tích từng số ra thừa số nguyên tố sau đó ta tìm được các ước của nó

Hướng dẫn giải

Câu a

225 = 3² . 5² chia hết cho 3 và 5;           

Câu b

1800 = 2³ . 3² . 5² chia hết cho 2, 3, 5;                    

Câu c

1050 = 2 . 3 . 5² . 7 chia hết cho 2, 3, 5, 7;                

Câu d

3060 = 2² . 3² . 5 . 17 chia hết cho 2, 3, 5, 17

Cho số \(a = 2^3. 5^2. 11\). Mỗi số \(4, 8, 16, 11, 20\) có là ước của \(a\) hay không ? 

Phương pháp giải

Nếu a chia hết cho b thì b là ước của a.

Hướng dẫn giải

Ta có: \(a = 2^3. 5^2. 11\) 

Khi đó

\(4\) là một ước của \(a\) vì \(4\) là một ước của \(2^3=8\);

\(8 = 2^3\) là một ước của \(a\)

\(16=2^4\) không phải là ước của a (vì a chia hết cho lũy thừa cao nhất của \(2\) là \(2^3=8\)) 

\(11\) là một ước của \(a\)

\(20\) cũng là ước của \(a\) vì \(a = 2^3.5^2.11 = 2.2.2.5.5.11 \)\(= 2.(2.2.5).5.11 = 2.20.5.11 \,⋮ \,20.\)

a) Cho số \(a = 5 . 13\). Hãy viết tất cả các ước của \(a\).

b) Cho số \(b = 2^5\). Hãy viết tất cả các ước của \(b\).

c) Cho số \(c = 3^2 .7\). Hãy viết tất cả các ước của \(c\).

Phương pháp giải

Nếu có số tự nhiên a chia hết cho số tự nhiên b thì ta nói a là bội của b, còn b là ước của a.

Hướng dẫn giải

a) \(a\) có các ước là \(1, 5, 13, 5.13=65\)

b) Các ước của \(2^5\) là \(1, 2, 2^2, 2^3, 2^4, 2^5\) hay \(1, 2, 4, 8, 16, 32\)

c) Các ước của \(3^2. 7\) là \(1, 3,  7,3^2, 3 . 7, 3^2. 7\) hay \(1, 3, 7,9, 21, 63.\)

Phân tích các số sau ra thừa số nguyên tố rồi tìm tập hợp các ước của mỗi số:

\(51\);  \(75\);   \( 42\);   \(30\).

Phương pháp giải

• Bước 1: phân tích từng số ra thừa số nguyên tố theo cột dọc.
• Bước 2: Dựa vào kết quả ta tìm được các ước của mỗi số đó.

Hướng dẫn giải

51 = 3 . 17, Ư(51) = {1; 3; 17; 51};

75 = 3 . 25, Ư(75) = {1; 3; 5; 25; 15; 75};

42 = 2 . 3 . 7, Ư(42) = {1; 2; 3; 7; 6; 14; 21; 42};

30 = 2 . 3 . 5, Ư(30) = {1; 2; 3; 5; 6; 10; 15; 30}

a) Tích của hai số tự nhiên bằng \(42\). Tìm mỗi số.

b) Tích của hai số tự nhiên \(a\) và \(b\) bằng \(30\). Tìm \(a\) và \(b\), biết rằng \(a < b\).

Phương pháp giải

Ta phân tích số 42 và 30 ra thừa số nguyên tố, tìm ước của mỗi số. Từ đó ta tìm đước các cặp số thỏa mãn yêu cầu bài toán.

Hướng dẫn giải

Câu a

Ta có: \(42 = 2.3.7\) 

Do đó ta có thể viết:

\(42 = (2.3). 7 = 6.7\)

\(42 = (2.7).3 = 14.3\)

\(42 = (3.7).2 = 21.2\)

\(42 = 1.(2.3.7) = 1.42\)

Câu b

Theo giả thiết tích của hai số tự nhiên \(a\) và \(b\) bằng \(30\) nên ta có: \(30= a . b\).

Điều này có nghĩa là \(a\) và \(b\) là ước của \(30\); và \(a

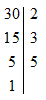
Ước của \(30\) là: \(1;2;3;5;6;10;15;30\)

Do \(a

+) \(a = 1, b = 30\); 

+) \(a = 2, b = 15\);

+) \(a = 3, b = 10\);

+) \(a = 5, b = 6\).

Tâm có \(28\) viên bi. Tâm muốn xếp số bi đó vào túi sao cho số bi ở các túi đều bằng nhau. Hỏi Tâm có thể xếp \(28\) viên bi đó vào mấy túi ? (kể cả trường hợp xếp vào một túi).

Phương pháp giải

Bài toán thực chất là ta đi tìm ước của 28 là ra được số túi cần tìm

Hướng dẫn giải

Vì số bi ở các túi bằng nhau nên số túi phải là ước của \(28\)

Ta có \(28 = 2^2. 7\). 

Suy ra tập hợp các ước của \(28\) là \(\left\{1; 2; 4; 7; 14; 28\right\}\).

Vậy số túi có thể là: \(1, 2, 4, 7, 14, 28\).

(Giải thích: ví dụ có \(3\) túi thì \(28\) viên bi chia đều cho \(3\) túi đó mỗi túi có \(9\) viên bi và thừa \(1\) không cho được vào túi nào, nếu cho vào bất kì túi nào thì số bi trong các túi đều không bằng nhau. Do đó để số bi trong mỗi túi bằng nhau thì \(28\) chia hết cho tổng số túi, hay số túi là ước của \(28\)).

a) Phân tích số \(111\) ra thừa số nguyên tố rồi tìm tập hợp các ước của \(111\).

b) Thay dấu * bởi chữ số thích hợp:

\(\overline{**} . * = 111\).

Phương pháp giải

Phân tích số 111 ra thừa số nguyên tố bằng cột dọc rồi ta tìm được ước của 111. 

Hướng dẫn giải

Câu a: Ta có

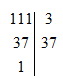
Nên \(111 = 3 . 37\).

Tập hợp \(Ư(111) =\left\{1; 3; 37; 111\right\}\).

Câu b: Từ \(\overline{**} . * = 111\) ta suy ra \(\overline{**}\) và  \(*\) đều là ước của \(111\)

Mà ước có 2 chữ số của 111 chỉ có 37.

Do đó \(\overline{**}=37,\) suy ra \(*=3\)

Vậy ta có: \(37 . 3 = 111\).