Giải bài tập SGK Toán 10 Bài 3: Tích của vectơ với một số

Cho hình bình hành ABCD. Chứng mỉnh rằng

 $\overrightarrow{AB}$ $+$ $\overrightarrow{AC}$ $+$ $\overrightarrow{AD}$ $=2\overrightarrow{AC}$

Phương pháp giải

Quy tắc hình bình hành: Nếu cho ABCD là hình bình hành thì: $\overrightarrow {AB}  + \overrightarrow {AD}  = \overrightarrow {AC} .$

Hướng dẫn giải

Ta có: $\overrightarrow {AB}  + \overrightarrow {AC}  + \overrightarrow {AD}  = (\overrightarrow {AB}  + \overrightarrow {AD} ) + \overrightarrow {AC} \,\,(1)$

Theo quy tắc hình bình hành ta có:

$\overrightarrow {AD}  + \overrightarrow {AB}  = \overrightarrow {AC} \,\,\,\,\,\,\,\,\,\,(2)$

Từ (1) và (2) ta có:

$\begin{array}{l}\overrightarrow {AB}  + \overrightarrow {AC}  + \overrightarrow {AD}  = \overrightarrow {AC}  + \overrightarrow {AC} \\ \Leftrightarrow \overrightarrow {AB}  + \overrightarrow {AC}  + \overrightarrow {AD}  = 2\overrightarrow {AC} \end{array}$

2. Giải bài 2 trang 17 SGK Hình học 10

Cho AK và BM là hai trung tuyến của tam giác ABC. Hãy phân tích các vectơ $\overrightarrow{AB},\overrightarrow{BC},\overrightarrow{AC}$, theo hai vectơ sau $\overrightarrow{u}=\overrightarrow{AK},\overrightarrow{v}=\overrightarrow{BM}$.

Phương pháp giải

• Sử dụng tính chất của đường trung tuyến.
• Với 3 điểm $A, \, \, B, \, \, C$ bất kì ta luôn có: $\overrightarrow {AB}  + \overrightarrow {BC}  = \overrightarrow {AC} .$

Hướng dẫn giải

Do tính chất trung điểm nên từ giả thiết ta có:

$\left\{ \begin{array}{l}2\overrightarrow {AK}  = \overrightarrow {AB}  + \overrightarrow {AC} \\2\overrightarrow {BM}  = \overrightarrow {BA}  + \overrightarrow {BC} \end{array} \right.$

$\Leftrightarrow \left\{ \begin{array}{l}\overrightarrow {AB}  - \overrightarrow {CA}  = 2\vec u\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(1)\\ - \overrightarrow {AB}  + \overrightarrow {BC}  = 2\vec v\,\,\,\,\,\,\,\,\,\,\,(2)\end{array} \right.$

Mặt khác, ta có: $\overrightarrow {AB}  + \overrightarrow {BC}  + \overrightarrow {CA}  = \overrightarrow {AC}  + \overrightarrow {CA}$

$\Leftrightarrow \,\,\overrightarrow {AB}  + \overrightarrow {BC}  + \overrightarrow {CA}  = \vec 0\,\,\,\,\,\,\,\,\,\,\,\,\,\,(3)$

Từ (1) và (2) ta có:

$(\overrightarrow {AB}  - \overrightarrow {CA} ) + ( - \overrightarrow {AB}  + \overrightarrow {BC} ) = 2\vec u + 2\vec v$

$\Leftrightarrow \overrightarrow {AB}  - \overrightarrow {CA}  - \overrightarrow {AB}  + \overrightarrow {BC}  = 2\vec u + 2\vec v$

$\Leftrightarrow  - \overrightarrow {CA}  + \overrightarrow {BC}  = 2\vec u + 2\vec v$ (4)

Từ (2) và (3) ta có:

$- \overrightarrow {AB}  + \overrightarrow {BC}  + \overrightarrow {AB}  + \overrightarrow {BC}  + \overrightarrow {CA}  = 2\vec v$

$\Leftrightarrow 2\overrightarrow {BC}  + \overrightarrow {CA}  = 2\vec v\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(5)$

Từ (4) và (5) suy ra:

$- \overrightarrow {AB}  + \overrightarrow {BC}  + 2\overrightarrow {BC}  + \overrightarrow {CA}  = 2\vec u + 2\vec v + 2\vec v$

$\Leftrightarrow 3\overrightarrow {BC}  = 2\vec u + 4\vec v \Leftrightarrow \overrightarrow {BC}  = \frac{2}{3}\vec u + \frac{4}{3}\vec v\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(6)$

Từ (5) và (6) ta có

$\frac{4}{3}\vec u + \frac{8}{3}\vec v\, + \overrightarrow {CA}  = 2\vec v \Rightarrow \overrightarrow {CA}  =  - \frac{4}{3}\vec u + \frac{2}{3}\vec v\,\,\,\,\,\,\,\,\,(7)$

Từ (7) và (1), ta có được:

$\overrightarrow {AB}  + \frac{4}{3}\vec u + \frac{2}{3}\vec v = 2\vec u \Leftrightarrow \overrightarrow {AB}  = \frac{2}{3}\vec u - \frac{2}{3}\vec v$

Kết luận

$\overrightarrow {AB}  = \frac{2}{3}\vec u - \frac{2}{3}\vec v$

$\overrightarrow {BC}  = \frac{2}{3}\vec u + \frac{4}{3}\vec v$

$\overrightarrow {CA}  =  - \frac{4}{3}\vec u - \frac{2}{3}\vec v$

Trên đường thẳng chứa cạnh BC của tam giác ABC lấy một điểm M sao cho $\overrightarrow{MB}=3\overrightarrow{MC}$. Hãy phân tích vectơ  $\overrightarrow{AM}$ theo hai vectơ  $\overrightarrow{u}=\overrightarrow{AB}, \overrightarrow{v}=\overrightarrow{AC}$.

Phương pháp giải

Với 3 điểm $A, \, \, B, \, \, C$ bất kì ta luôn có: $\overrightarrow {AB}  + \overrightarrow {BC}  = \overrightarrow {AC} .$

Hướng dẫn giải

Ta có: $\overrightarrow {AM}  = \overrightarrow {AC}  + \overrightarrow {CM} \,\,\,\,\,\,\,\,\,(1)$

Vì $\overrightarrow {CM}$ cùng hướng với $\overrightarrow {BC} ,$ hơn nữa $\left| {\overrightarrow {BC} } \right| = 2\left| {\overrightarrow {CM} } \right|,$ nên

$\overrightarrow {CM}  = \frac{1}{2}\overrightarrow {BC}  = \frac{1}{2}(\overrightarrow {AC}  - \overrightarrow {AB} )\,\,\,\,\,\,(2)$

Từ (1) và (2) ta có

$\overrightarrow {AM}  = \overrightarrow {AC}  + \frac{1}{2}(\overrightarrow {AC}  - \overrightarrow {AB} ) \Leftrightarrow \overrightarrow {AM}  = \frac{3}{2}\overrightarrow {AC}  - \frac{1}{2}\overrightarrow {AB} .$

Vậy $\overrightarrow {AM}  = \frac{3}{2}\vec v - \frac{1}{2}\vec u.$

Gọi AM là trung tuyến của tam giác ABC  và D là trung điểm của đạn AM. Chứng minh rằng:

a) $2\overrightarrow{DA}+\overrightarrow{DB}+\overrightarrow{DC}=\overrightarrow{0}$

b) $2\overrightarrow {OA}  + \overrightarrow {OB}  + \overrightarrow {OC}  = 4\overrightarrow {OD}$, với $O$ là điểm tùy ý

Phương pháp giải

ới $M$ là trung điểm của $AB$ ta có:

+) $\overrightarrow {MA}  + \overrightarrow {MB}  = \overrightarrow 0 .$

+) Với mọi điểm $O$ bất kì ta có: $\overrightarrow {OA}  + \overrightarrow {OB}  = 2\overrightarrow {OM} .$

Hướng dẫn giải

Câu a

Vì $M$ là trung điểm của $BC$ nên:

Ta có

$\overrightarrow {DB}  + \overrightarrow {DC}  = 2\overrightarrow {DM}$

Mặt khác, do $D$ là trung điểm của đoạn $AM$ nên

$\overrightarrow {DM}  =  - \overrightarrow {DA}$ $\Leftrightarrow \overrightarrow {DM}  + \overrightarrow {DA}  = \overrightarrow 0$

Khi đó: $2\overrightarrow {DA}  + \overrightarrow {DB}  + \overrightarrow {DC}  = 2\overrightarrow {DA}  + 2\overrightarrow {DM}$$= 2\left( {\overrightarrow {DA}  + \overrightarrow {DM} } \right) = \overrightarrow 0$

Câu b: Ta có

 $2\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}=4\overrightarrow{OD}$ $\Leftrightarrow 2(\overrightarrow{OA}-\overrightarrow{OD})+( \overrightarrow{OB}-\overrightarrow{OD})+( \overrightarrow{OC}-\overrightarrow{OD})=\overrightarrow{0}$

$\Leftrightarrow 2 \overrightarrow{DA}+\overrightarrow{OB}+\overrightarrow{OC}= \overrightarrow{0}$luôn đúng theo câu a

Vậy:$\Leftrightarrow 2\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}= 4\overrightarrow{OD}$, với O là điểm tùy ý

Gọi M và N lần lượt là trung điểm các cạnh AB và CD của tứ giác ABCD. Chứng minh rằng: $2\overrightarrow{MN}=\overrightarrow{AC}+\overrightarrow{BD}= \overrightarrow{BC}+\overrightarrow{AD}$

Phương pháp giải

Với $M$ là trung điểm của $AB$ ta có

• $\overrightarrow {MA}  + \overrightarrow {MB}  = \overrightarrow 0 .$
• Với mọi điểm $O$ bất kì ta có: $\overrightarrow {OA}  + \overrightarrow {OB}  = 2\overrightarrow {OM} .$

Hướng dẫn giải

N là trung điểm của CD

$2\overrightarrow{MN}=\overrightarrow{MC}+\overrightarrow{MD}$        (1)

Theo quy tắc 3 điểm, ta có:

$\overrightarrow{MC}=\overrightarrow{MA}+\overrightarrow{AC}$             (2)

$\overrightarrow{MD}=\overrightarrow{MB}+\overrightarrow{BD}$           (3)

Từ (1), (2), (3) ta có:  $2\overrightarrow{MN}=\overrightarrow{AC}+\overrightarrow{BD}+ \overrightarrow{MA}+\overrightarrow{MB}$

vì M là trung điểm của Ab nên:  $\overrightarrow{MA}+\overrightarrow{MB}=\overrightarrow{0}$

Suy ra:  $2\overrightarrow{MN}=\overrightarrow{AC}+\overrightarrow{BD}$

Chứng minh tương tự, ta có  $2\overrightarrow{MN}=\overrightarrow{BC}+\overrightarrow{AD}$

Chú ý: Sau khi chứng minh $2\overrightarrow{MN}=\overrightarrow{AC}+\overrightarrow{BD}$ta chỉ cần chứng minh thêm $\overrightarrow{AC}+\overrightarrow{BD}= \overrightarrow{BC}+\overrightarrow{AD}$ cũng được

Ta có: $\overrightarrow{AC}+\overrightarrow{BD}= \overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{BA}+\overrightarrow{AD}$ $=\overrightarrow{BC}+\overrightarrow{AD}+\overrightarrow{AB}+\overrightarrow{BA}= \overrightarrow{BC}+\overrightarrow{AD}+\overrightarrow{AA}$

Vì $\overrightarrow{AA}=\overrightarrow{0}$nên ta có: $\overrightarrow{AC}+\overrightarrow{BD}= \overrightarrow{BC}+\overrightarrow{AD}$ và $2 \overrightarrow{MN}=\overrightarrow{AC}+\overrightarrow{BD}= \overrightarrow{BC}+\overrightarrow{AD}$

Cho hai điểm phân biệt A và B. Tìm điểm K sao cho $3\overrightarrow{KA}+2\overrightarrow{KB}=\overrightarrow{0}$

Phương pháp giải

Với 3 điểm $A, \, B, \, C$ ta có $\overrightarrow {AB}  = k\overrightarrow {AC}$ thì $A, \, B, \, C$ thẳng hàng.

+) Nếu $k>0$ thì $\overrightarrow {AB}$ và $\overrightarrow {AC}$ cùng hướng.

+) Nếu $k<0$ thì $\overrightarrow {AB}$ và $\overrightarrow {AC}$ ngược hướng.

Hướng dẫn giải

Ta có: $3\overrightarrow{KA}+2\overrightarrow{KB}=\overrightarrow{0} \Rightarrow 3\overrightarrow{KA}=-2\overrightarrow{KB}\Rightarrow \overrightarrow{KA}=\frac{2}{3}\overrightarrow{KB}$

Đẳng thức này chứng tỏ hi vec tơ $\overrightarrow{KA},\overrightarrow{KB}$ là hai vec tơ ngược hướng, do đó K thuộc đoạn AB

Ta lại có: $\left |\overrightarrow{KA} \right |=-\frac{2}{3} \left |\overrightarrow{KB} \right | \Rightarrow KA=\frac{2}{3}KB$

Vậy K là điểm chia trong đoạn thẳng AB theo tỉ số $\frac{2}{3}$

Cho tam giác ABC. Tìm điểm M sao cho $\overrightarrow{MA}+\overrightarrow{MB}+2\overrightarrow{MC}=\overrightarrow{0}$

Phương pháp giải

Với $I$ là trung điểm của $AB$ ta có:

• $\overrightarrow {IA}  + \overrightarrow {IB}  = \overrightarrow 0 .$
• Với mọi điểm $O$ bất kì ta có: $\overrightarrow {OA}  + \overrightarrow {OB}  = 2\overrightarrow {OI} .$

Hướng dẫn giải

Gọi D là trung điểm của cạnh AB, ta có:

 $\overrightarrow{MA}+\overrightarrow{MB}=2\overrightarrow{MD}$

Đẳng thức đã cho trở thành:

 $2\overrightarrow{MD}+\overrightarrow{MC}=\overrightarrow{0}$ $\Rightarrow \overrightarrow{MD}+\overrightarrow{MC}=\overrightarrow{0}$

Đẳng thức này chứng tỏ M là trung điểm của CD

Cho lục giác ABCDEF. Gọi M, N, P, Q, R, S lần lượt là trung điểm của các cạnh AB, BC, CD, DE, EF, FA. Chứng minh rằng hai tam giác MPR và NQS có cùng trọng tâm.

Hướng dẫn giải

$MN$ là đường trung bình của tam giác $ABC$ nên ta có: $\overrightarrow {MN}  = {1 \over 2}\overrightarrow {AC}$

Tương tự ta có:        

$\eqalign{ & \overrightarrow {PQ} = {1 \over 2}\overrightarrow {CE} \cr & \overrightarrow {RS} = {1 \over 2}\overrightarrow {EA} \cr}$

$\eqalign{ & \Rightarrow \overrightarrow {MN} + \overrightarrow {PQ} + \overrightarrow {RS} \cr& = \frac{1}{2}\overrightarrow {AC}  + \frac{1}{2}\overrightarrow {CE}  + \frac{1}{2}\overrightarrow {EA} \cr&= {1 \over 2}\left( {\overrightarrow {AC} + \overrightarrow {CE} + \overrightarrow {EA} } \right)\cr& = \frac{1}{2}\left( {\overrightarrow {AE}  + \overrightarrow {EA} } \right) = {1 \over 2}\overrightarrow {AA} = \overrightarrow 0 \cr & \Rightarrow \overrightarrow {MN} + \overrightarrow {PQ} + \overrightarrow {RS} = \overrightarrow 0  \cr}$

Gọi $G$ là trọng tâm của tam giác $MPR$, ta có:

$\overrightarrow {GM}  + \overrightarrow {GP}  + \overrightarrow {GR}  = \overrightarrow 0 (2)$

Mặt khác 

$\eqalign{ & \overrightarrow {MN} = \overrightarrow {MG} + \overrightarrow {GN} \cr & \overrightarrow {PQ} = \overrightarrow {PG} + \overrightarrow {GQ} \cr & \overrightarrow {RS} = \overrightarrow {RG} + \overrightarrow {GS} \cr}$

$\Rightarrow \overrightarrow {MN}  + \overrightarrow {PQ}  + \overrightarrow {RS}$$= \left( {\overrightarrow {MG}  + \overrightarrow {PG}  + \overrightarrow {RG} } \right)$ $+ (\overrightarrow {GN}  + \overrightarrow {GQ} + \overrightarrow {GS})$

$= \overrightarrow 0  + \overrightarrow {GN}  + \overrightarrow {GQ}  + \overrightarrow {GS}$ $= \overrightarrow {GN}  + \overrightarrow {GQ}  + \overrightarrow {GS}$

(vì $\overrightarrow {MG}  + \overrightarrow {PG}  + \overrightarrow {RG}$ $=  - \overrightarrow {GM}  - \overrightarrow {GP}  - \overrightarrow {GR}$ $=  - \left( {\overrightarrow {GM}  + \overrightarrow {GP}  + \overrightarrow {GR} } \right) = \overrightarrow 0$)

$\Rightarrow \overrightarrow {MN}  + \overrightarrow {PQ}  + \overrightarrow {RS}$ $= \overrightarrow {GN}  + \overrightarrow {GQ}  + \overrightarrow {GS}$

Mà $\overrightarrow {MN} + \overrightarrow {PQ} + \overrightarrow {RS} = \overrightarrow 0$ nên 

$\overrightarrow {GN}  + \overrightarrow {GQ}  + \overrightarrow {GS}  = \overrightarrow 0$

Vậy $G$ là trọng tâm của tam giác $NQS.$

Vậy trọng tâm ΔMPR và ΔNQS trùng nhau.

Cho tam giác đều ABC có trọng tâm O và M là một điểm tùy ý trong tam giác. Gọi D,E,F lần lượt là chân đường vuông góc hạ từ M đến BC, AC, AB. Chứng minh rằng: $\overrightarrow{MD}+\overrightarrow{ME}+\overrightarrow{MF} =\frac{3}{2}\overrightarrow{MO}$

Hướng dẫn giải

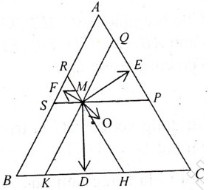
Qua M kẻ các đường thẳng song song với các cạnh của tam giác

A1B1 // AB;  A2C2 // AC;   B2C1 // BC

Dễ thấy các tam giác MB1C2; MA1C1;MA2B2 đều là các tam giác đều. Ta lại có MD B1C2 nên MD cũng là trung điểm thuộc cạnh B1C2 của tam giác MB1C2

Ta có 2 = + 

Tương tự: 2 = + 

               2 = +

⇒ 2( ++) = (+) + ( + ) + (+)

Tứ giác là hình bình hành nên

           +  = 

Tương tự: + = 

                 + = 

=> 2( ++) = ++

Vì O là trọng tâm bất kì của tam giác và M là một điểm bất kì nên

 ++ = 3.

Cuối cùng ta có: 

2( ++) = 3

⇒  ++ = 

Vậy ta được đpcm $\overrightarrow{MD}+\overrightarrow{ME}+\overrightarrow{MF} =\frac{3}{2}\overrightarrow{MO}$