Giải bài tập SGK Toán 9 Bài 5: Góc có đỉnh ở bên trong đường tròn. Góc có đỉnh ở bên ngoài đường tròn

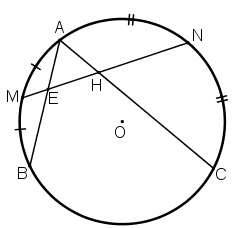
Cho đường tròn (O) và hai dây AB, AC. Gọi M, N lần lượt là điểm chính giữa của cung AB và cung AC. Đường thẳng MN cắt dây AB tại E và cắt dây AC tại H.

Chứng minh tam giác AEH là tam giác cân.

Phương pháp giải

Sử dụng định lý về số đo của góc có đỉnh ở bên trong đường tròn: "Số đo góc có đỉnh ở bên trong đường tròn bằng tổng số đo hai cung bị chắn"

Ta có: 

+) \(\widehat{AEH}=\dfrac{\text{sđ}\overset\frown{MB}+\text{sđ}\overset\frown{AN}}{2}\)

+) \( \widehat{AHE}=\dfrac{\text{sđ}\overset\frown{AM}+\text{sđ}\overset\frown{NC}}{2} \)

Chứng minh \( \widehat{AEH}=\widehat{AHE}\) suy ra tam giác AEH cân tại A.

Hướng dẫn giải

Theo định lý góc có đỉnh ở bên trong đường tròn ta có:

+) \(\widehat{AEH}=\dfrac{\text{sđ}\overset\frown{MB}+\text{sđ}\overset\frown{AN}}{2}\)

+) \( \widehat{AHE}=\dfrac{\text{sđ}\overset\frown{AM}+\text{sđ}\overset\frown{NC}}{2} \)

Lại có:  M, N là điểm chính giữa của cung AB và cung AC nên ta có:

+) \(\overset\frown{AM}=\overset\frown{MB} \)

+) \( \overset\frown{AN}=\overset\frown{NC} \)

Do vậy: \( \widehat{AEH}=\widehat{AHE}\) hay tam giác AEH cân tại A.

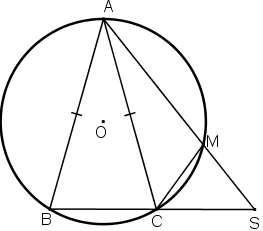
Cho đường tròn (O) và hai dây AB, AC bằng nhau. Trên cung nhỏ AC lấy một điểm M. Gọi S là giao điểm của AM và BC.

Chứng minh rằng: \(\widehat{ASC}=\widehat{MCA}\)

Phương pháp giải

Sử dụng định lý về số đo góc nội tiếp và góc có đỉnh nằm ở bên ngoài đường tròn.

Chứng minh được \(\widehat{ASC}=\dfrac{1}{2}\left( \text{sđ}\overset\frown{AB}-\text{sđ}\overset\frown{MC} \right)=\dfrac{1}{2}\left( \text{sđ}\overset\frown{AC} -\text{sđ}\overset\frown{MC} \right)=\dfrac{1}{2}.\text{sđ}\overset\frown{AM}=\widehat{ACM} \)

Hướng dẫn giải

Xét đường tròn (O) có:

\(\widehat{ASC}=\dfrac{\text{sđ}\overset\frown{AB}-\text{sđ}\overset\frown{MC}}{2}\)  (góc có đỉnh ở bên ngoài đường tròn chắn cung AB và cung MC)

\(\widehat{ACM}=\dfrac{1}{2}.\text{sđ}\overset\frown{AM}\) (góc nội tiếp chắn cung AM)

Lại có \(AB=AC\) (giả thiết) nên \(\overset\frown{AB}=\overset\frown{AC} \)

Do vậy, \(\widehat{ASC}=\dfrac{1}{2}\left( \text{sđ}\overset\frown{AB}-\text{sđ}\overset\frown{MC} \right)=\dfrac{1}{2}\left( \text{sđ}\overset\frown{AC} -\text{sđ}\overset\frown{MC} \right)=\dfrac{1}{2}.\text{sđ}\overset\frown{AM}=\widehat{ACM} \)

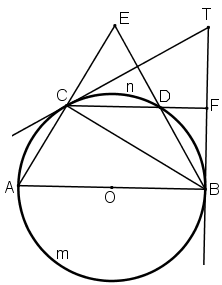
Trên một đường tròn, lấy liên tiếp ba cung AC, CD, DB sao cho \(sđ\overset\frown{AC}=sđ\overset\frown{CD}=sđ\overset\frown{DB}=60^o\). Hai đường thẳng AC và BD cắt nhau tại E. Hai tiếp tuyến của đường tròn tại B và C cắt nhau tại T. Chứng minh rằng:

a) \(\widehat{AEB}=\widehat{BTC}\)

b) CD là tia phân giác của \(\widehat{BCT}\)

Phương pháp giải

a) Xét đường tròn (O) có AB là đường kính nên \(\text{sđ}\overset\frown{AB}={{180}^{o}}\) 

Chứng minh được: \(\widehat{BTC}=\dfrac{1}{2}\left( \text{sđ}\overset\frown{CAB}-\text{sđ}\overset\frown{CDB} \right)\)

b) \(\widehat{DCT} \) là góc tạo bởi tia tiếp tuyến và dây cung chắn cung DC nên:

\(\widehat{DCT}=\dfrac{1}{2}.\text{sđ}\overset\frown{CD}\)

\(\widehat{DCB}\)  là góc nội tiếp chắn cung DB nên:

\(\widehat{DCB}=\dfrac{1}{2}.\text{sđ}\overset\frown{DB}\)

Chứng minh được: \(\widehat{DCT}=\widehat{DCB} \)

Hướng dẫn giải

a) Xét đường tròn (O) có AB là đường kính nên \(\text{sđ}\overset\frown{AB}={{180}^{o}}\) 

Ta có \( \widehat{AEB}\)  là góc có đỉnh ở bên ngoài đường tròn nên:

\(\widehat{AEB}=\dfrac{1}{2}\left( \text{sđ}\overset\frown{AB}-\text{sđ}\overset\frown{CD} \right)=\dfrac{1}{2}\left( {{180}^{o}}-{{60}^{o}} \right)={{60}^{o}} \)

\(\widehat{BTC} \) là góc có đỉnh ở bên ngoài đường tròn nên:

\( \begin{aligned} \widehat{BTC}&=\dfrac{1}{2}\left( \text{sđ}\overset\frown{CAB}-\text{sđ}\overset\frown{CDB} \right)\\&=\dfrac{1}{2}\left( \text{sđ}\overset\frown{AB}+\text{sđ}\overset\frown{AC}-\text{sđ}\overset\frown{DC}-\text{sđ}\overset\frown{DB} \right) \\ & =\dfrac{1}{2}\left( {{180}^{o}}+{{60}^{o}}-{{60}^{o}}-{{60}^{o}} \right)={{60}^{o}} \\ \end{aligned} \)

Vậy \(\widehat{AEB}=\widehat{BTC} \)

b) Ta có: 

\(\widehat{DCT} \) là góc tạo bởi tia tiếp tuyến và dây cung chắn cung DC nên:

\(\widehat{DCT}=\dfrac{1}{2}.\text{sđ}\overset\frown{CD}=\dfrac{1}{2}{{.60}^{o}}={{30}^{o}} \)

\(\widehat{DCB}\)  là góc nội tiếp chắn cung DB nên

\(\widehat{DCB}=\dfrac{1}{2}.\text{sđ}\overset\frown{DB}=\dfrac{1}{2}{{.60}^{o}}={{30}^{o}} \)

Suy ra \(\widehat{DCT}=\widehat{DCB} \)

Vậy CD là phân giác của góc \( \widehat{BCT} \)