Giải bài tập SGK Toán 8 Bài 2: Hình thang

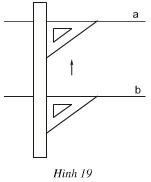
Dùng thước và êke, ta có thể kiểm tra được hai đường thẳng có song song với nhau hay không (xem hình 19). Trên hình 20, có những tứ giác nào là hình thang, có những tứ giác nào không là hình thang. Bằng cách nêu trên, hãy kiểm tra xem trong các tứ giác ở hình 20, tứ giác nào là hình thang

Phương pháp giải

Áp dụng

• Định nghĩa hai đường thẳng song song: là hai đường thẳng không có điểm chung.
• Định nghĩa hình thang: Hình thang là tứ giác có hai cạnh đối song song.

Hướng dẫn giải

Các bước tiến hành

- Xét xem cần phải kiểm tra hai cạnh nào thuộc hai đường thẳng song song với nhau.

- Đặt mép cạnh góc vuông của êke trùng với một trong hai cạnh cần kiểm tra.

- Đặt mép thước trùng với mép cạnh góc vuông còn lại của êke.

- Giữ nguyên vị trí thước, dời êke để xét xem cạnh góc vuông của êke có trùng với cạnh còn lại mà ta cần kiểm tra của tứ giác. Nếu chúng trùng nhau thì tứ giác đó là hình thang.

Bằng cách kiểm tra trên ta có kết quả như sau

Tứ giác \(ABCD\) có cạnh \(AB\) song song với cạnh \(DC\) nên tứ giác \(ABCD\) là hình thang.

Tứ giác \(IKMN\) có cạnh \(IN\) song song với cạnh \(KM\) nên tứ giác \(IKMN\) là hình thang.

Tứ giác \(EFGH\) không là hình thang vì không có cặp cạnh nào song song với nhau.

Tìm \(x\) và \(y\) trên hình \(21\), biết rằng \(ABCD\) là hình thang có đáy là \(AB\) và \(CD.\)

Phương pháp giải

Áp dụng các tính chất của một đường thẳng cắt hai đường thẳng song song: hai góc trong cùng phía bù nhau, hai góc đồng vị bằng nhau, hai góc so le trong bằng nhau.

Hướng dẫn giải

Vì \(ABCD\) là hình thang có đáy là \(AB\) và \(CD\) nên \(AB//CD\)

\(a)\) Ta có: \(AB//DC\) (chứng minh trên) 

\(\Rightarrow \widehat A +\widehat D=180^0\) (hai góc trong cùng phía bù nhau)

\(\Rightarrow x + {80^0} = {180^0}\) 

\(\Rightarrow x = {180^0} - {80^0} = {100^0}\)

Ta có: \(AB//DC\) (chứng minh trên)

\(\Rightarrow \widehat C +\widehat B=180^0\) (hai góc trong cùng phía bù nhau)

\(\Rightarrow y + {40^0} = {180^0}\)

\(\Rightarrow y = {180^0} - {40^0} = {140^0}\)

\(b)\) Vì \(AB//DC\) (chứng minh trên)

\(\Rightarrow x ={70^0} \) (hai góc đồng vị bằng nhau)

\(\Rightarrow y ={50^0} \) (hai góc so le trong bằng nhau)

\(c)\) Ta có \(AB//DC\) (chứng minh trên)

\( \Rightarrow \widehat B + \widehat C = {180^0}\) (hai góc trong cùng phía bù nhau)

\(\Rightarrow x + {90^0} = {180^0}\)

\(\Rightarrow x = {180^0} - {90^0} = {90^0}\)

Ta có \(AB//DC\) (chứng minh trên)

\(\Rightarrow \widehat D + \widehat A = {180^0}\) (hai góc trong cùng phía bù nhau)

\( \Rightarrow y + {65^0} = {180^0}\)

\(\Rightarrow y = {180^0} - {65^0} = {115^0}\)

Hình thang \(ABCD\) (\(AB // CD\)) có \(\widehat{A}-\widehat{D}={20^0}\)   , \(\widehat{B}=2\widehat{C}\). Tính các góc của hình thang.

Phương pháp giải

Áp dụng tính chất: Nếu một đường thẳng cắt hai đường thẳng song song thì tổng hai góc trong cùng phía bù nhau.

Hướng dẫn giải

Vì \(AB//CD\) nên \(\widehat A + \widehat D = {180^0}\)  (1) (hai góc trong cùng phía bù nhau)

Ta có \(\widehat A - \widehat D = {20^0}\) (giả thiết) 

\(\begin{array}{l}
\Rightarrow \widehat A = \widehat D + {20^0}\;\;(2)\\\text{Thay (2) vào (1) ta được:}\\
\Rightarrow \widehat A + \widehat D = \widehat D + {20^0} + \widehat D\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\, = 2\widehat D + {20^0} = {180^0}\\
\Rightarrow \widehat D = \left( {{{180}^0} - {{20}^0}} \right):2 = {80^0}.
\end{array}\)

Thay \(\widehat{D}=80^0\) vào \(\widehat{A}=20^0\) +\(\widehat{D}\) ta được \(\widehat{A}=20^0 + 80^0= 100^0\)

Lại có \(\widehat{B}=2\widehat{C}\)     (3) 

Do \(AB//CD\) nên \(\widehat{B}+\widehat{C}=180^0\)   (4) (hai góc trong cùng phía bù nhau)

Thay (3) vào (4) ta được:

\(2\widehat{C}+\widehat{C}=180^0\)

hay \(3\widehat C = {180^0}\Rightarrow\widehat C = {180^0}:3 = {60^0}\)

Do đó \(\widehat{B}=2\widehat{C}= 2.60^0 =120^0\)

Tứ giác ABCD có AB= BC và tia phân giác của góc A. Chứng minh rằng ABCD là hình thang.

Phương pháp giải

Áp dụng

• Dấu hiệu nhận biết hình thang: Hình thang là tứ giác có hai cạnh đối song song.
• Chứng minh hai đường thẳng song song ta chứng minh cặp góc so le trong bằng nhau.

Hướng dẫn giải

Ta có \(AB = BC\) (giả thiết)

Suy ra  \(∆ABC\) cân tại \(B\) (định nghĩa tam giác cân)

Nên \(\widehat{A_{1}}=\widehat{C_{1}}\) (1) (tính chất tam giác cân) 

Lại có, \(AC\) là tia phân giác của \(\widehat{A}\) (giả thiết) nên suy ra \(\widehat{A_{1}}= \widehat{A_{2}}\) (2) (tính chất tia phân giác )

Từ (1) và (2) suy ra \(\widehat{C_{1}}=\widehat{A_{2}}\) mà hai góc này ở vị trí so le trong nên \(BC // AI\)

Vậy tứ giác \(ABCD\) là hình thang.

Đố hình 22 là hình vẽ một chiếc thang trên hình vẽ có bao nhiêu hình thang?

Phương pháp giải

Áp dụng dấu hiệu nhận biết hình thang: Hình thang là tứ giác có hai cạnh đối song song.

Hướng dẫn giải

Từ hình 22 ta có: \(AB//CD//EF//GH\)

Nên ta có tất cả \(6\) hình thang, đó là: \(ABDC, CDFE, EFHG,\) \(ABFE, CDHG, ABHG.\)