Giải bài tập SGK Toán 7 Bài 1: Tổng ba góc của một tam giác

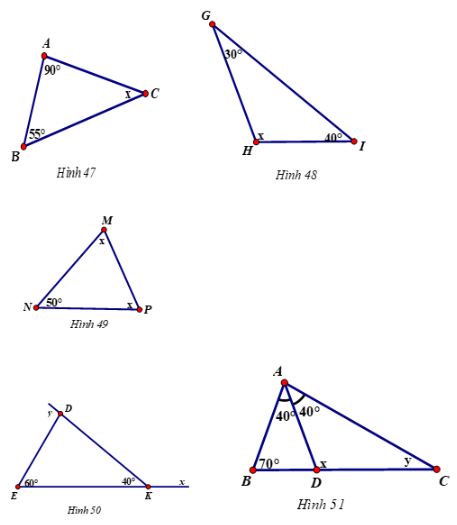
Tính số đo \(x\) và \(y\) ở các hình \(47,48,49,50,51\):

Phương pháp giải:

Áp dụng:

- Định lí: Tổng ba góc của một tam giác bằng \({180^0}\)

- Mỗi góc ngoài của một tam giác bằng tổng hai góc trong không kề với nó.

Hướng dẫn giải:

Hình 47

Áp dụng định lí tổng ba góc của một tam giác vào \(\Delta ABC\) ta được:
\(x + {{90}^0} + {{55}^{0}} = {{180}^0}\)
\(\Rightarrow x = {{180}^0} - \left( {{{90}^0} + {{55}^0}} \right) = {{35}^0}\)

Hình 48 

Áp dụng định lí tổng ba góc của một tam giác vào \(\Delta GHI\) ta được:

\(x + {\rm{ }}{{40}^0} + {\rm{ }}{{30}^0} = {\rm{ }}{{180}^0}\)
\( \Rightarrow {\rm{ }}x = {\rm{ }}{{180}^0}{\rm{ - }}\left( {{\rm{ }}{{40}^0} + {\rm{ }}{{30}^0}} \right) = {\rm{ }}{{110}^0}\)

Hình 49

Áp dụng định lí tổng ba góc của một tam giác vào \(\Delta MNP\) ta được:

\(x + {\rm{ }}x + {\rm{ }}{{50}^0} = 180^0\)
\( \Rightarrow {\rm{ }}2x = {\rm{ }}{{180}^0} - {{50}^0} = {{130}^0}\) 

\( \Rightarrow x= {{130}^0}:2 = {65}^0\)

Hình 50

Vì \(y\) là góc ngoài \(\Delta DEK\) tại đỉnh \(D\) nên ta có:

\(y = {\rm{ }}{60^0} + {\rm{ }}{40^0} = {\rm{ }}{100^0}\)

Góc \(x\) và \(\widehat{DKE}\) là hai góc kề bù nên:

\(x + {{40}^0} ={180}^{0}\)

\( \Rightarrow x = {{180}^0} - {{40}^{0}} = 140^0\)

Hình 51

Áp dụng định lí tổng ba góc của một tam giác vào \(\Delta  ABC\) ta có:

\(\widehat A + \widehat B + \widehat C=180^0\)

\(({40^0} + {\rm{ }}{40^0}){\rm{ }} + {\rm{ }}{70^0} + {\rm{ }}y{\rm{ }} = {180^0}\)

\( \Rightarrow y+  150^0 =180^0\)

\( \Rightarrow y = {180^{0}} - {\rm{ }}{150^0} = {\rm{ }}{30^{0}}\)

Áp dụng định lí tổng ba góc của một tam giác vào \(\Delta  ACD\) ta có:

\(x + {\rm{ }}{40^0} + {\rm{ }}{30^0} = {\rm{ }}{180^0}\)

\( \Rightarrow x = {\rm{ }}{180^0} - ({\rm{ }}{40^0} + {\rm{ 3}}{0^0}) = {\rm{ }}{110^0}\)

Cho tam giác \(ABC\) có \(\widehat{B}= 80^0\), \(\widehat{C}=  30^0\). Tia phân giác của góc \(A\) cắt \(BC\) ở \(D\). Tính \(\widehat{ADC},\widehat{ADB}\).

Phương pháp giải:

Áp dụng định lí:

- Tổng ba góc của một tam giác bằng \({180^0}\);

- Mỗi góc ngoài của một tam giác bằng tổng hai góc trong không kề với nó;

- Hai góc kề bù có tổng số đo bằng \({180^0}\).

Hướng dẫn giải:

Áp dụng định lí tổng ba góc của một tam giác vào \(\Delta ABC\) ta có:

\(\widehat {BAC} + \widehat B + \widehat C = {180^0}\)

\(\widehat{BAC}= 180^0- (\widehat{B}+\widehat{C})\) \(= 180^0-( 80^0+ 30^0)= 70^0\) 

Vì \(AD\) là tia phân giác của \(\widehat{BAC}\) nên \(\widehat{A_{1}}=\widehat{A_{2}}=\dfrac{\widehat{BAC}}2=\dfrac{70^{0}}2= 35^0\)

Vì \(\widehat{ADC}\) là góc ngoài tại đỉnh \(D\) của \(\Delta ABD\) nên

\(\widehat{ADC} = \widehat{B} + \widehat{A_{1}}\) (góc ngoài của một tam giác bằng tổng hai góc trong không kề với nó)  

\( \Rightarrow \widehat {ADC}=80^0+ 35^0= 115^0\)

\(\widehat{ADC}\) và \(\widehat{ADB}\) là hai góc kề bù 

Do đó \(\widehat{ADB}+ \widehat{ADC}=  180^0\)

\(\Rightarrow \widehat{ADB}=  180^0- \widehat{ADC}= 180^0-115^0\)\(=65^0\)

Vậy \(\widehat {ADC}= 115^0;\)\(\widehat {ADB}= 65^0;\)

Cho hình \(52.\) Hãy so sánh: 

a) \(\widehat{BIK}\) và \(\widehat{BAK}\).

b) \(\widehat{BIC}\) và \(\widehat{BAC}\) 

Phương pháp giải:

Áp dụng định lí: Mỗi góc ngoài của một tam giác bằng tổng hai góc trong không kề với nó.

Hướng dẫn giải:

Câu a: Ta có \(\widehat{BIK}\) là góc ngoài tại đỉnh \(I\) của \(\Delta  BAI\). 

Nên  \(\widehat{BIK}=\widehat{BAI }+\widehat{ABI }> \widehat{BAI }\)

Mà \(\widehat{BAK}=\widehat{BAI }\) 

Vậy \(\widehat{BIK}>\widehat{BAK}\) (1) 

Câu b: Ta có \(\widehat{CIK }\) là góc ngoài tại đỉnh \(I\) của \(\Delta AIC\)

nên \(\widehat{CIK }=\widehat{CAI}+\widehat{ICA}>\widehat{CAI}\)

Hay  \(\widehat{CIK }>  \widehat{CAI}\)  (2)

Từ (1) và (2) ta có:

\(\widehat{BIK}  + \widehat{CIK } > \widehat{BAK } + \widehat{CAI}\)

\(\Rightarrow \widehat{BIC} > \widehat{BAC}\).

Tháp nghiêng Pi - da ở Italia nghiêng \(5^0\)  so với  phương thẳng đứng (h.53). Tính số đo của góc \(ABC\) trên hình vẽ. 

Phương pháp giải:

Trong tam giác vuông có hai góc nhọn phụ nhau.

Hướng dẫn giải:

Xét \(ABC\) vuông ở \(C\) nên ta có: 

\(\widehat{A}+ \widehat{B}=  90^0\) (vì hai góc nhọn trong tam giác vuông phụ nhau).

\( \Rightarrow 5^0+\widehat{B} =  90^0\)

\(\Rightarrow\widehat{B}= {90^0} - {5^0} = {85^0}\)

 Hay \(\widehat {ABC} = {85^o}\)

Ta gọi tam giác có ba góc nhọn là tam giác nhọn, tam giác có một góc tù là tam giác tù. Gọi tên tam giác nhọn, tam giác tù, tam giác vuông trên hình 54. 

Phương pháp giải:

+ Áp dụng định lí: Tổng ba góc của một tam giác bằng \({180^0}\)

+ Sử dụng định nghĩa tam giác nhọn, tam giác tù, tam giác vuông để gọi tên các tam giác. 

Hướng dẫn giải:

 a) Áp dụng định lí tổng ba góc của một tam giác vào tam giác \(ABC\) ta được:

$$\eqalign{
& \widehat A + \widehat B + \widehat C = {180^0} \cr
& \Rightarrow \widehat A = {180^0} - \widehat B - \widehat C \cr&\;\;\;\;\;\;\;\;\,= {180^0} - {62^0} - {28^0} = {90^0} \cr} $$

Do đó tam giác \(ABC\) vuông tại \(A\).

b)  Áp dụng định lí tổng ba góc của một tam giác vào tam giác \(DEF\) ta được:                

$$\eqalign{
& \widehat D + \widehat E + \widehat F = {180^0} \cr
& \Rightarrow \widehat D = {180^0} - \widehat E - \widehat F \cr&\;\;\;\;\;\;\;\;\;\,= {180^0} - {45^0} - {37^0} = {98^0} \cr} $$

Vì \(\widehat D = {98^0}>90^0\) nên là góc tù. 

Do đó tam giác \(DEF\) tù.               

c) Áp dụng định lí tổng ba góc của một tam giác vào tam giác \(HKI\) ta được:      

$$\eqalign{
& \widehat H + \widehat K + \widehat I = {180^0} \cr
& \Rightarrow \widehat H = {180^0} - \widehat K - \widehat I \cr&\;\;\;\;\;\;\;\;\;\,= {180^0} - {38^0} - {62^0} = {80^0} \cr} $$

Vì \(\widehat H = {80^0} < {90^0},\widehat I = {62^0} < {90^0},\)\(\widehat K = {38^0} < {90^0}\)

Do đó tam giác \(HKI\) nhọn.

Tìm các số đo \(x\) ở các hình sau: 

Phương pháp giải:

Áp dụng:

- Trong tam giác vuông có hai góc nhọn phụ nhau.

- Mỗi góc ngoài của một tam giác bằng tổng hai góc trong không kề với nó.

Hướng dẫn giải:

Hình 55

Xét \(\Delta AHI\,\text{ có }\,\widehat H = {90^0}\) ta có: 

\(\widehat{A}+\widehat{AIH}= 90^0\) (1) (tổng hai góc nhọn của tam giác vuông phụ nhau)

Xét \(\Delta BKI\,\text{ có }\,\widehat K = {90^0}\) ta có:

\(\widehat{B} + \widehat{BIK} = 90^0\)   (2) (tổng hai góc nhọn của tam giác vuông phụ nhau)

Từ (1) và (2) suy ra: \(\widehat{A}+\widehat{AIH}=\widehat{B} + \widehat{BIK}\)

Mà  \(\widehat{AIH}= \widehat{BIK}\) (hai góc đối đỉnh)

Nên suy ra \( \widehat{B}=\widehat{A}=40^0\)

Vậy \(\widehat{B}=x= 40^0\) 

Hình 56

Xét \(\Delta ABD\,\text{ có }\,\widehat {ADB} = {90^0}\) ta có:

 \(\widehat{ABD} +\widehat{A}= 90^0\) (4) (tổng hai góc nhọn của tam giác vuông phụ nhau)

Xét \(\Delta ACE\,\text{ có }\,\widehat {AEC} = {90^0}\) ta có:

\(\widehat{ACE}+ \widehat{A}=90^0\)  (5) (tổng hai góc nhọn của tam giác vuông phụ nhau)

Từ (4) và (5) suy ra \(\widehat{ACE} = \widehat{ABD}=25^0\)

Vậy \(x=25^0\) 

Hình 57

Ta có: \(\widehat{NMP}=\widehat{NMI} + \widehat{PMI}=  90^0\)  (6)

Xét \(\Delta MNI\,\text{ có }\,\widehat {MIN} = {90^0}\) ta có :

\(\widehat{N } +  \widehat{NMI}=  90^0\)  (7) (tổng hai góc nhọn của tam giác vuông phụ nhau) 

Từ (6) và (7) suy ra \(\widehat{N } = \widehat{PMI}=60^0\)

Vậy \(x=60^0\)

Hình 58

Xét \(\Delta AHE\,\text{ có }\,\widehat {AHE} = {90^0}\) ta có :

\(\widehat{E } + \widehat{A}=90^0\) (tổng hai góc nhọn của tam giác vuông phụ nhau) 

\(\widehat{E }= 90^0- \widehat{A} = 90^0- 55^0= 35^0\)

Vì \(\widehat{KBH }\) là góc ngoài tại đỉnh \(B\) của tam giác \(BKE\) nên 

\(\widehat{KBH }=\widehat{BKE}+ \widehat{E }\)\(= 90^0+ 35^0= 125^0\)

Vậy \(x=125^0\)

Cho tam giác \(ABC\) vuông tại \(A\). Kẻ \(AH\) vuông góc với \(BC\) (\(H\in BC\)).

a) Tìm các cặp góc phụ nhau trong hình vẽ.

b) Tìm các cặp góc nhọn bằng nhau trong hình vẽ.

Phương pháp giải:

Áp dụng định lí: Trong tam giác vuông có hai góc nhọn phụ nhau.

Hướng dẫn giải:

Câu a: Tam giác \(ABC\) vuông tại \(A\) nên ta có \(\widehat{B } + \widehat{C }= 90^0;\) \(\widehat {{A_1}} + \widehat {{A_2}} = {90^o}\)

Hay  \(\widehat{B }\), \(\widehat{C }\) phụ nhau; \(\widehat {{A_1}}\), \(\widehat {{A_2}}\) phụ nhau.

Tam giác \(AHB\) vuông tại \(H\) nên ta có \(\widehat{B }+ \widehat{A_{1} }=  90^0\) 

Hay \(\widehat{B }\), \(\widehat{A_{1} }\) phụ nhau.  

Tam giác \(AHC\) vuông tại \(H\) nên ta có \(\widehat{A_{2} }+ \widehat{C } = 90^0\)  

Hay \(\widehat{A_{2} }\), \(\widehat{C }\) phụ nhau.

Câu b: 

Ta có \(\widehat{B } + \widehat{C }= 90^0\) 

         \(\widehat{B }+ \widehat{A_{1} }=  90^0\)

\(\Rightarrow \widehat{A_{1} }=\widehat{C }\)

Ta có: \(\widehat{B } + \widehat{C }=90^0\)  và  \(\widehat{A_{2} }+ \widehat{C } =90^0\)

\(\Rightarrow \widehat{A_{2} } = \widehat{B }\) 

Cho tam giác \(ABC\) có \(\widehat{B}=\widehat{C}= 40^0\). Gọi \(Ax\) là tia phân giác của góc ngoài ở đỉnh \(A\), Hãy chứng tỏ \(Ax// BC\). 

Phương pháp giải:

Áp dụng:

- Mỗi góc ngoài của một tam giác bằng tổng hai góc trong không kề với nó.

- Chứng minh hai đường thẳng song song ta chứng minh cặp góc so le trong bằng nhau.

Hướng dẫn giải:

Gọi \(\widehat{CAD} \) là góc ngoài tại đỉnh \(A\) của tam giác \(ABC\).

Theo định lý về góc ngoài, ta có: 

\(\widehat{CAD }  =  \widehat{B}+ \widehat{C}\)\(=  40^0+ 40^0=80^0\)

Lại có, \(Ax\) là phân giác \(\widehat{CAD }\)

nên \(\widehat{A_{2} }= \dfrac{1}2\widehat{CAD}=\dfrac{80}2=40^0\)

\( \Rightarrow \widehat {{A_2}}=\widehat{BCA }=40^o\)

Mà hai góc này ở vị trí so le trong nên \(Ax// BC\).

Hình 59 biểu diễn mặt cắt ngang  của một con đê để đo góc nhọn \(MOP\) tạo bởi mặt phẳng nghiêng của con đê với phương nằm ngang, người ta dùng thước chữ \(T\) và đặt như hình vẽ (\(OA\perp AB\)). Tính góc \(MOP\), biết rằng dây dọi \(BC\) tạo với trục \(BA\) một góc \(\widehat{ABC }= 32^0\) 

Phương pháp giải:

Áp dụng:

- Trong tam giác vuông có hai góc nhọn phụ nhau.

- Hai góc đối đỉnh thì bằng nhau.

Hướng dẫn giải:

Tam giác \( ABC\) vuông tại \(A\) nên \(\widehat{ABC}+ \widehat{ACB}= 90^0\) (1) (trong tam giác vuông có hai góc nhọn phụ nhau)

Tam giác \( DOC\) vuông tại \(D\) nên \(\widehat{COD}+ \widehat{OCD}= 90^0\) (2) (trong tam giác vuông có hai góc nhọn phụ nhau) 

Ta lại có \( \widehat{ACB}=\widehat{OCD}\) (hai góc đối đỉnh)    (3)

Từ (1), (2), (3) suy ra \(\widehat{COD}= \widehat{ABC}=32^0\).

Vậy \(\widehat{MOP}=\widehat{COD}=32^0\)