Giải bài tập SGK Toán 6 Bài 8: Đường tròn

Trong hình 48, ta có hai đường tròn $(O;2cm)$ và $(A;2cm)$ cắt nhau tại $C, D.$ Điểm $A$ nằm trên đường tròn tâm $O.$  

Hình 48

a) Vẽ đường tròn tâm $C,$ bán kính $2cm.$

b) Vì sao đường tròn $(C;2cm)$ đi qua $O,A?$

Hướng dẫn giải

Câu a:

Mở khẩu độ compa bằng 2cm. Vẽ đường tròn tâm C bán kính 2cm

Xem hình bên:

Câu b:

Vì hai đường tròn $(O; 2cm)$ và $(A; 2cm)$ cắt nhau tại $C$ nên:

- Điểm $C$ thuộc $(O; 2cm) ⇒ OC = 2cm$ do đó $O$ thuộc $(C; 2cm)$

- Điểm $C$ thuộc $(A; 2cm) ⇒ AC = 2cm$ do đó $A$ thuộc $(C; 2cm)$

Vậy đường tròn $(C; 2cm)$ đi qua hai điểm $O$ và $A.$

Trên hình 49, ta có hai đường tròn $(A;3cm)$ và $(B;2cm)$ cắt nhau tại $C, D.$ $AB = 4cm.$ Đường tròn tâm $A,B$ lần lượt cắt đoạn thẳng $AB$ tại $K, I.$

Hình 49

a) Tính $CA, CB, DA,DB.$

b) $I$ có phải là trung điểm của đoạn thẳng $AB$ không?

c) Tính $IK.$

Hướng dẫn giải

Câu a:

Vì hai đường tròn (A; 3cm) và (B; 2cm) cắt nhau tại C; D nên:

Hai điểm $C$ và $D$ nằm trên đường tròn $(A; 3cm)$ nên $CA = DA = 3cm$

Hai điểm $C$ và $D$ nằm trên đường tròn $(B; 2cm)$ nên $CB = DB = 2cm$

Câu b:

Đường tr:òn (B; 2cm) cắt đoạn AB tại I nên I nằm trên đường tròn (B; 2cm), suy ra BI = 2cm.

Trên tia $BA$ có: $BI = 2cm, AB = 4cm$

Suy ra \(BI

Suy ra $AI + IB = AB$ 

$\Rightarrow AI = AB - IB = 4 - 2 = 2cm$

Do đó: $AI = BI \,(=2cm)$ (2)

Từ (1) và (2) suy ra $I$ là trung điểm của đoạn thẳng $AB.$

Câu c:

Đường tròn (A; 3cm) cắt đoạn AB tại K nên K thuộc đường tròn (A ; 3cm) , suy ra AK = 3cm. 

Trên tia $AB$ có $AI = 2cm, AK = 3cm.$

Vì $AI < AK$ ($2cm<3cm)$ nên điểm $I$ nằm giữa hai điểm $A$ và $K.$

Suy ra $AI + IK = AK$

$\Rightarrow  IK = AK - AI = 3 - 2 = 1cm$

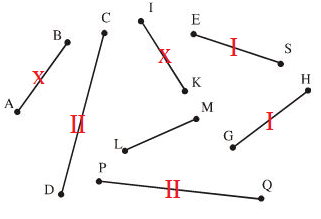
Với compa, hãy so sánh các đoạn thẳng trong hình 50 rồi đánh cùng một dấu cho các đoạn thẳng bằng nhau. 

Hình 50

Hướng dẫn giải

Cách so sánh: Dùng compa với độ mở sao cho hai mũi nhọn compa trùng với hai đầu của một đoạn thẳng. Với cùng độ mở đó ta có thể so sánh với độ dài đoạn thẳng thứ hai.

Kết quả so sánh: $LM < AB = IK < ES = GH < CD = PQ$

Đánh dấu như trong hình: 

(Chúng ta có 3 cặp đoạn thẳng bằng nhau: $AB = IK; ES = GH; CD = PQ$)

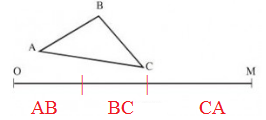
Đố: Xem hình 51. So sánh $AB + BC + AC$ với $OM$ bằng mắt rồi kiểm tra bằng dụng cụ.

Hình 51

Hướng dẫn giải

- So sánh bằng mắt: $AB + BC + AC = OM$

- Kiểm tra (bằng thước đo hay compa): Trên tia $OM$ kể từ $O$ ta đặt liên tiếp ba đoạn thẳng có độ dài lần lượt bằng $AB, BC, CA.$ Ta thấy điểm cuối trùng với $M.$

Vậy $AB + BC + AC = OM.$

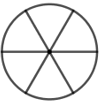
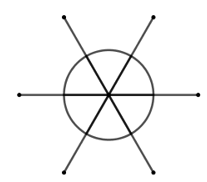
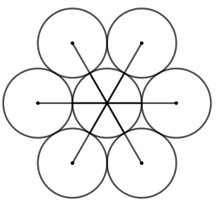
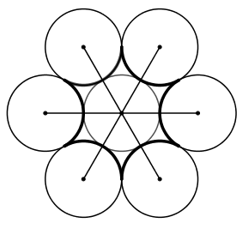
Vẽ lại các hình sau (đúng kích thước  như hình đã cho) 

Hình 52

Hướng dẫn giải

Câu a:

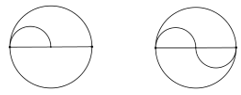
+ Vẽ đường tròn bán kính $1,2cm.$ 

+ Vẽ một đường kính của đường tròn.

+ Xác định trung điểm của hai bán kính. Vẽ hai cung tròn có bán kính bằng một nửa bán kính của đường tròn ban đầu.

+ Tô màu như hình vẽ.

Câu b:

Trước hết vẽ hình vuông. Lấy giao điểm của hai đường chéo làm tâm vẽ 5 đường tròn có bán kính lần lượt bằng bán kính của 5 đường tròn đã cho. Rồi tô màu như hinh đẫ cho.

Câu c:

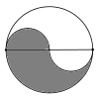
+ Vẽ đường tròn ở giữa

+ Chia đường tròn thành 6 phần bằng nhau bằng cách vẽ các đường kính tạo với nhau 1 góc 60⁰.

+ Kéo dài các đường kính, trên các đường kéo dài đó lấy các điểm sao cho độ dài đoạn thẳng từ tâm đến các điểm đó bằng hai lần bán kính đường tròn.

+ Vẽ các đường tròn tâm là các điểm vừa lấy, bán kính bằng bán kính đường tròn ban đầu.

+ Dùng bút nét to vẽ lại các cung tròn được tô đậm như hình dưới

d) + Vẽ môt đường tròn đường và chia thành 6 phần bằng nhau như phần c)

+ Nối các đoạn thẳng như hình vẽ.

+ Xác định trung điểm các đoạn thẳng vừa vẽ để làm tâm đường tròn.

+ Vẽ các nửa đường tròn.