Giải bài tập SGK Toán 12 Bài 1: Khái niệm về mặt tròn xoay

Cho đường tròn tâm O bán kính r nằm trên mặt phẳng (P). Từ những điểm M thuộc đường tròn này ta kẻ những đường thẳng vuông góc với (P). Chứng minh rằng những đường thẳng như vậy nằm trên một mặt trụ tròn xoay. Hãy xác định trục và bán kính của mặt trụ đó.

Phương pháp giải

Dựa vào định nghĩa mặt trụ tròn xoay (SGK - 35)

Trong mặt phẳng (P) cho hai đưuòng thẳng \(\Delta\) và \(l\) song song với nhau, cách nhau một khoảng bằng \(r\). Khi quay mặt phẳng \((P)\) xung quanh \(\Delta\) thì đường thẳng \(l\) sinh tra một mặt tròn xoay được gọi là mặt trụ tròn xoay. Đường thẳng \(\Delta\) gọi là trục, đường thẳng \(l\) là đường sinh và \(r\) là bán kính của mặt trụ.

Hướng dẫn giải

Xét đường thẳng ∆ đi qua điểm O và vuông gó với mặt phẳng (P). Gọi l là đưởng thẳng đi qua M0 ε (C) và l vuông góc với (P).

Do đó l // ∆. Quay mặt phẳng (Q) tạo bởi l và ∆ quanh đường thẳng ∆, thì đường thẳng l vạch lên một mặt trụ tròn xoay.

Mặt trụ này chứa tất cả những đường thẳng đi qua các điểm M ε (C) và vuông góc với (P). Trục của mặt trụ là ∆ và bán kính của trụ bằng r.

Trong mỗi trường hợp sau đây, hãy gọi tên các hình tròn xoay hoặc khối tròn xoay sinh ra bởi:

a) Ba cạnh của hình chữ nhật khi quay quanh đường thẳng chứa cạnh thứ tư.

b) Ba cạnh của một tam giác cân khi quay quanh trục đối xứng nó.

c) Một tam giác vuông kể cả các điểm trong của tam giác vuông đó khi quay quanh đường thẳng chứa một cnah góc vuông.

d) Một hình chữ nhật kể cả các điểm trong của hình chữ nhật đó khi quay quanh đường thẳng chứa một cạnh

Phương pháp giải

Dựa vào định nghĩa mặt tròn xoay: Mặt trụ và mặt nón.

Hướng dẫn giải

Câu a

Hình trụ tròn xoay có đường cao là cạnh thứ tư còn bán kính hình trụ bằng độ dài của cạnh kề với cạnh thứ tư đó.

Câu b

Hình nón tròn xoay có chiều cao bằng chiều cao của tam giác cân, cond bán kính đáy bằng một nửađộ dài cạnh đáy của tam giác cân đó.

Câu c

Khối nón tròn xoay

Câu d

Khối trụ tròn xoay.

Cho hình nón tròn xoay có đường cao h = 20 cm, bán kính đáy r = 25 cm.

a) Tính diện tích xung quanh của hình nón đã cho.

b) Tính thể tích của khối nón được tạo bởi hình nón đó.

c) Một thiết diện đi qua đỉnh của hình nón có khoảng cách từ tâm của đáy đến mặt phẳng chứa thiết diện là 12 cm. Tính diện tích thiết diện đó.

Phương pháp giải

• Diện tích xung quanh của hình nón: \({S_{xq}} = \pi rl\) trong đó \(r\) là bán kính đáy và \(l\) là độ dài đường sinh của hình nón.
• Thể tích của khối nón: \(V = \frac{1}{3}\pi {r^2}h\)  trong đó \(r\) là bán kính đáy và \(h\) là độ dài đường cao của hình nón.
• Thiết diện đi qua đỉnh của hình nón là tam giác cân. Tính diện tích tam giác cân \(S = \frac{1}{2}ah\).

Hướng dẫn giải

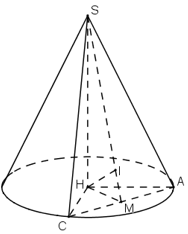
Câu a

Đường sinh l của hình nón là:

l = \(\small 5\sqrt{41}\) (cm).

Diện tích xung quanh của hình nón là:

\({S_{xq}} = \pi rl = 125\pi \sqrt {41} \left( {c{m^2}} \right)\)

Câu b

Vnón = \(\frac{{625.20\pi }}{3} = \frac{{12500\pi }}{3}\left( {c{m^3}} \right)\)

Câu c

Gọi hình nón đã cho có đỉnh là S và H là tâm đường tròn đáy.

Thiết diện đi qua đỉnh S là tam giác SAC (với A và C thuộc đường tròn đáy)

Gọi M là trung điểm của AC.

Ta có: \(\left\{ \begin{array}{l}
AC \bot HM\\
AC \bot SH
\end{array} \right. \Rightarrow AC \bot mp\left( {SHM} \right)\)

\( \Rightarrow \left( {SAC} \right) \bot \left( {SHM} \right)\) theo giao tuyến SM

Trong mp(SHM) kẻ \(HI \bot SM \Rightarrow HI \bot \left( {SAC} \right)\)

Do đó, d( H; (SAC))= HI = 12

Trong tam giác vuông SHM ta có:

\(\begin{array}{l}
\frac{1}{{H{I^2}}} = \frac{1}{{S{H^2}}} + \frac{1}{{H{M^2}}} \Rightarrow \frac{1}{{H{M^2}}} = \frac{1}{{H{I^2}}} - \frac{1}{{S{H^2}}}\\
 \Rightarrow \frac{1}{{H{M^2}}} = \frac{1}{{{{12}^2}}} - \frac{1}{{{{20}^2}}} = \frac{1}{{225}} \Rightarrow HM = 15
\end{array}\)

Trong tam giác vuông HAM ta có:

\(A{M^2} = H{A^2} - H{M^2} = {25^2} - {15^2} = 400\) nên AM = 20(cm)

Ta có:

\(\begin{array}{l}
\sin \widehat {HSM} = \frac{{HM}}{{SM}} = \frac{{HI}}{{SH}}\\
 \Rightarrow SM = \frac{{HM.SH}}{{HI}} = \frac{{15.20}}{{12}} = 25
\end{array}\)

Do đó, diện tích thiết diện SAC là:

\(\begin{array}{l}
{S_{SAC}} = \frac{1}{2}.AC.SM = AM.SM\\
 = 20.25 = 500\left( {c{m^2}} \right)
\end{array}\)

Trong không gian cho hai điểm A, B cố định và có độ dài AB = 20 cm. Gọi d là một đường thẳng thay đổi luôn luôn đi qua A và cách B một khoảng  bằng 10 cm. Chứng tỏ rằng đường thẳng d luôn luôn nằm trên một mặt nón, hãy xác định trục và góc ở đỉnh của mặt nón đó.

Phương pháp giải

Dựa vào định nghĩa hình nón: Trong mặt phẳng \((P)\) cho hai đường thẳng \(d\) và \(\Delta\) cắt nhau tại điểm \(O\) vào tạo thành góc \(\beta\) với \({0^0}<{\beta}<{90^0}\).

Khi quay mặt phẳng \((P)\) xung quanh \(\Delta\) thì đường thẳng \(d\) sinh ra một mặt tròn xoay được gọi là mặt nón tròn xoay đỉnh \(O\).

Đường thẳng \(\Delta\) gọi là trục, đường thẳng \(d\) gọi là đường sinh và góc \(2\beta\) gọi là góc ở đỉnh của mặt nón đó.

Hướng dẫn giải

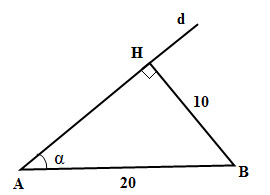
Kẻ \(BH \bot d\) ta có \(BH = 10cm\). Gọi \(\alpha  = \widehat {BAH}\)

Ta có \(\sin \alpha  = {{BH} \over {AB}} = {1 \over 2} \Rightarrow \alpha  = {30^0}=const\).

Đường thẳng \(d\) cắt AB tại điểm A và tạo thành góc \(30^0\) nên đường thẳng \(d\) luôn thuộc mặt nón nhận đường thẳng \(AB\) làm trục và có góc ở đỉnh bằng \(2α = 60^0\)

Một hình trụ có bán kính đáy r = 5cm và có khoảng cách giữa hai đáy bằng 7 cm.

a) Tính diện tích xung quanh của hình trụ và thể tích của khối trụ được tạo nên.

b) Cắt khối trụ bởi một mặt phẳng song song với trục và cách trục 3 cm. Hãy tính diện tích của thiết diện được tạo nên.

Phương pháp giải

Diện tích xung quanh của hình trụ \({S_{xq}} = 2\pi rh\), 

Thể tích khối trụ \(V = \pi {r^2}h\).

Với \(r;h\) lần lượt là bán kính đáy và độ dài đường cao của hình trụ.

Hướng dẫn giải

Câu a

Theo đầu bài, hình trụ có chiều cao h = 7 cm và bán kính đáy r = 5 cm.

Vậy diện tích xung quanh bằng: Sxq= πrh = 35π (cm²)

Thể tích của khối trụ là:

V = πr²h = 175π (cm³)

Câu b

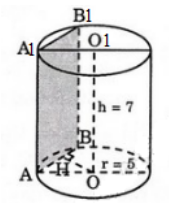
Mặt phẳng (P) song song với trục và cách trục 3cm, cắt hình trụ theo thiết diện là tứ giác AA1B1B.

Gọi H là trung điểm của AB.

Ta có: \(\left\{ {\begin{array}{*{20}{l}}
{OH \bot AB}\\
{OH \bot A{A_1}}
\end{array}} \right. \Rightarrow OH \bot \left( {A{A_1}{B_1}B} \right)\)

Suy ra: OH = d(O; (AA₁B₁B)), (1)

Lại có: OO₁// mp (AA₁B₁B), (2)

Từ (1) và (2) suy ra: OH = d(O; (AA₁B₁B)= d( OO1, (AA1B1B) ) = 3 cm

Xét tam giác AOH vuông tại H ta có:

AH² = AO² - OH² = 5² -3² = 16

⇒ AH = 4cm ⇒ AB = 2AH = 8cm

Diện tích của thiết diện cần tính là:

SAA₁B₁B = AB. AA₁ = 8.7 = 56 (cm²)

Cắt một hình nón bằng một mặt phẳng qua trục của nó ta được thiết diện là một tam giác đều canh 2a. Tính diện tích xung quanh và thể tích của hình nón đó.

Phương pháp giải

• Tính độ dài đường sinh \(l\) và bán kính đáy \(r\) của hình nón.
• Tính độ dài đường cao của hình nón, sử dụng công thức \(h = \sqrt {{l^2} - {r^2}} \).
• Tính diện tích xung quanh và thể tích của hình nón đó: \({S_{xq}} = \pi rl,\,\,V = \frac{1}{3}\pi {r^2}h\)

Hướng dẫn giải

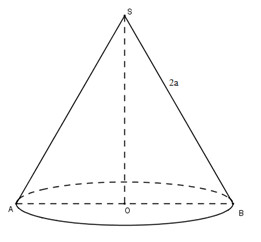
Theo đề bài, đường kính của hình tròn đáy của nón bằng \(\displaystyle 2a\)

Vậy bán kính \(\displaystyle r = a\) và độ dài đường sinh của hình nón \(\displaystyle l = 2a\)

Suy ra chiều cao của hình nón: \(\displaystyle h = \sqrt {{l^2} - {r^2}}  = \sqrt {4{a^2} - {a^2}}  = a\sqrt 3 \)

Vậy diện tích xung quanh của hình nón là: \(\displaystyle S_{xq} = πrl = π.a.2a=2a^2π\)

Thể tích khối nón là: \(\displaystyle V = {1 \over 3}\pi {r^2}.h = {1 \over 3}\pi {a^2}.a\sqrt 3  = {{\pi {a^3}\sqrt 3 } \over 3}\)

Một hình trụ có bán kính r và chiều cao \(h = r \sqrt {3}\)

a) Tính diện tích xung quanh và diện tích toàn phần của hình trụ

b) TÍnh thể tích khối trụ tạo nên bởi hình trụ đã cho.

c) Cho hai điểm A và B lần lượt nằm trên hai đường tròn đáy sao cho góc giữa đường thẳng AB và trục của hình trụ bằng 300. TÍnh khoảng cách giữa đường thẳng AB và trục của hình trụ

Phương pháp giải

Áp dụng công thức

• \({S_{xq}} = 2\pi rh,\,\,{S_{tp}} = 2\pi rh + \pi {r^2}\) với \(r;h\) lần lượt là bán kính đáy và độ dài đường cao của hình trụ.
• \(V = \pi {r^2}h\).
• Xác định khoảng cách giữa AB và \({O_1}{O_2}\) bằng cách xác định đường vuông góc chung giữa hai đường thẳng đó.

Hướng dẫn giải

Câu a

Theo công thức ta có

\(\small S_{xq} = 2\pi.r.h = 2\sqrt{3} \pi.r^2\)

\({S_t}_p = 2\pi .r.h + 2\pi .{r^2} = 2\sqrt 3 \pi .{r^2} + 2\pi .{r^2} = 2(\sqrt 3  + 1)\pi .{r^2}\) ( đơn vị thể tích)

Câu b

 \(\small V_{{tru}} = \pi.R^2.h = \sqrt{3} \pi r^3\)

Câu c

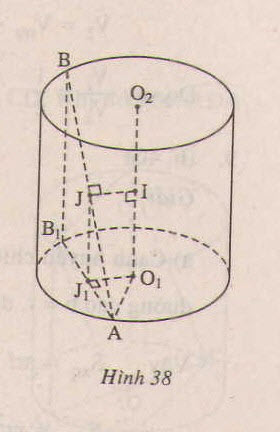
Giả sử trục của hình trụ là O₁O₂ và A nằm trên đường tròn tâm O₁, B nằm trên đường tròn tâm O₂; I là trung điểm của O₁O₂, J là trung điểm của AB. Khi đó IJ là đường vuông góc chung của O₁O₂ và AB. Hạ BB₁ vuông góc với đáy, J₁ là hình chiếu vuông góc của J xuống đáy.

Ta có J₁ là trung điểm của AB₁, O₁J₁ = IJ.

Theo giả thiết \(\widehat {{B_1}BA}\) = 30^0.

do vậy: AB₁ = BB₁.tan 30⁰ = \(\frac{{\sqrt 3 }}{3}h\) = r.

Xét tam giác vuông O₁J₁A vuông tại J_1, ta có: \({O_1}{J_1}^2 = {O_1}{A^2} - A{J_1}^2 = {r^2} - \frac{{{r^2}}}{2} = \frac{3}{4}{r^2}\)

Vậy khoảng cách giữa AB và O₁O₂: \(\frac{{\sqrt 3 }}{2}r\)

Một hình trụ có hai đáy là hai hình tròn (O;r) và (O';r). Khoảng cách giữa hai đáy là \(\small OO' = r.\sqrt{3}.\) Một hình nón có đỉnh là O' và có đáy là hình tròn (O;r).

a) Gọi S1 là diện tích xung quanh của hình trụ và S2 là diện tích xung quanh của hình nón, hãy tính tỷ số \(\small \frac{S_2}{S_1}\)

b) Mặt xung quanh của hình nón chia khối trụ thành hai phần, hãy tính tỷ số thể tích hai phần đó.

Phương pháp giải

• Diện tích xung quanh của hình trụ: \({S_{xq}} = 2\pi Rh\) với \(R;h\) lần lượt là bán kính đáy và chiều cao của hình trụ.
• Diện tích xung quanh của hình nón: \({S_{xq}} = \pi rl\) với \(r;l\) lần lượt là bán kính đáy và độ dài đường sinh của hình nón.
• Tính thế tích của khối nón: \({V_1} = \dfrac{1}{3}\pi {r^2}h\) và thể tích của hình trụ: \(V = \pi {r^2}h\)

Hướng dẫn giải

Câu a

Độ dài đường sinh của nón

\(l =\sqrt{h^2+r^2} =\sqrt{3r^2+r^2}= 2r\);

\(S_1 = 2\pi r.h = 2\sqrt{3}\pi r^2\).

\(S_2 = \pi rl = 2\pi r^22\). 

( Ở đó S1, S2 là diện tích xung quanh của hình trụ, hình nón).

Vậy: \(\frac{S_1}{S_2}=\sqrt{3}\)

Câu b

Gọi V₁ là thể tích khối nón, V₂ là thể tích phần còn lại của khối trụ.

Ta có: \(V_{kt}= \pi .r^2.h=.\pi r^3.h.\sqrt{3}\) (đơn vị thể tích)

\(V_{kn}= \frac{1}{3}.\pi .r^3.h=\frac{1}{3}.\pi.r^3\sqrt{3}\)

\(V=V_{kt}-V_{kn}=\pi.r^3.\frac{2\sqrt{3}}{3}\)

Do vậy \(\frac{V_{kn}}{V}=\frac{1}{2}\)

Căt hình nón đỉnh S bởi mặt phẳng đi qua trục ta được một tam giác vuông cân có cạnh huyền bằng \(a \sqrt {2}\).

a) Tính diện tích xuang quanh, diện tích đáy và thể tích của khối nón twong ứng.

b) Cho một dây cung BC và đường tròn đáy hình nón sao cho mặt phẳng (SBC) tạo với mặt phẳng chứa đáy hình nón một góc 60. Tính diện tích hình vuông và mặt phẳng đáy.

Phương pháp giải

Tính diện tích xung quanh \({S_{xq}} = \pi rl\), diện tích đáy \({S_đ} = \pi {r^2}\) và thể tích của khối nón: \(V = \dfrac{1}{3}\pi {r^2}h\).

Hướng dẫn giải

Câu a

Cạnh huyền chính bằng đường kính đáy do vậy bán kính đáy r = \(\frac{{a\sqrt 2 }}{2}\) và đường cao h = r, đường sinh l = a.

Vậy Sxq = πrl = \(\frac{\sqrt{2}}{2}\pi a^2\) ( đơn vị diện tích)

Sđáy = \(\pi r^{2}\) = \(\pi \frac{a^{2}}{2}\) ( đơn vị diện tích);

Vnón = \(\frac{1}{3}\pi r^{2}h\) \(= \frac{\sqrt{2}}{12} a^{3}\) ( đơn vị thể tích)

Câu b

Gọi tâm đáy là O và trung điểm cạnh BC là I

Theo giả thiết, \(\widehat {SIO}\) = 60⁰

Ta có diện tích ∆ SBC là: S = (SI.BC)/2

Ta có SO + SI.sin60⁰ = \(\frac{{\sqrt 3 }}{2}\).SI

Vậy \(SI = \frac{2}{{\sqrt 3 }}SO = \frac{{\sqrt 6 }}{3}a\)

Ta có ∆ OIB vuông ở I và BO = r = \(\frac{{a\sqrt 2 }}{2}\)

OI = SI.cos60⁰ = \(\frac{{\sqrt 6 }}{6}a\)

\(B{I^2} = B{O^2} - O{I^2} = \frac{{{a^2}}}{3}\)

Vậy BI = \(\frac{a}{{\sqrt 3 }}\) và BC = \(\frac{2a}{{\sqrt 3 }}\)

Do đó S = \(\frac{{SI.BC}}{2}\) = \(\frac{{\sqrt 2 }}{3}{a^2}\) (đơn vị diện tích)

Cho hình trụ có bán kính r và có chiều cao cũng bằng r. Một hình vuông ABCD có hai cạnh AB và CD lần lượt là các dây cung của hai đường tròn đáy, còn cạnh BC và AD không phải là đường sinh của hình trụ. Tính diện tích của hình vuông đó và cosin của góc giữa mặt phẳng chứa hình vuông và mặt phẳng đáy.

Phương pháp giải

• Dựa vào định lí Pitago tính độ dài IB, từ đó suy ra độ dài đường chéo AC và BD của hình vuông.
• Tính độ dài cạnh của hình vuông và diện tích hình vuông đó.
• Xác đinh góc giữa hai mặt phẳng: Gọi \(E\) là trung điểm của \(AB\), chứng minh góc giữa \((ABCD)\) và mặt đáy bằng góc \(IEO\).

Hướng dẫn giải

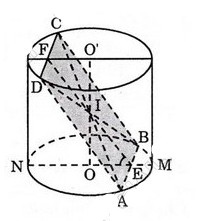
Do tính chất đối xứng của \((ABCD)\) nên \((ABCD)\) cắt \(OO'\) tại trung điểm \(I\) của \(OO'\). \(I\) cũng là giao điểm của hai đường chéo \(AC,BD\).

Xét tam giác vuông \(IOB\) ta có: \(IB^2=IO^2+OB^2\)

\(\Rightarrow IB=\sqrt {{{\left( {{r \over 2}} \right)}^2} + {r^2}}  = {{r\sqrt 5 } \over 2}\)

\(\Rightarrow AC=BD=2IB=r\sqrt5\).

Do ABCD là hinh vuông nên \(AB= \dfrac{{AC}}{{\sqrt 2 }}={{r\sqrt {10} } \over 2}\)

Vậy \(S_{ABCD}={AB}^2={{5{r^2}} \over 2}\).

Gọi \(E\) là trung điểm của \(AB\) 

\(\Rightarrow OE\bot AB, IE\bot AB\).

\(\Rightarrow \widehat {IEO}\) là góc giữa \((ABCD)\)  và mặt đáy của hình trụ.

Ta có: \(IE = \dfrac{1}{2}AD ={{r\sqrt {10} } \over 4}, OI={r\over 2}\).

Xét tam giác vuông IOE có: \(OE = \sqrt {I{E^2} - O{I^2}} \) \( = \sqrt {{{\left( {\dfrac{{r\sqrt {10} }}{4}} \right)}^2} - {{\left( {\dfrac{r}{2}} \right)}^2}}\) \(  = \dfrac{{r\sqrt 6 }}{4}\)

\(cos\widehat {IEO}={{OE}\over {IE}}={\sqrt{15}\over5}\)