Giải bài tập SGK Toán 12 Bài 3: Khái niệm về thể tích của khối đa diện

Tính thể tích khối tứ diện đều cạnh a.

Phương pháp giải

• Gọi \(AH\) là đường cao hạ từ đỉnh A của tứ diện đều \(ABCD\) \(\left({H \in (BCD)} \right)\).
• Do tứ diện ABCD đều, chứng minh H là trọng tâm tam giác \(ABC\).
• Sử dụng định lí Pytago tính độ dài \(AH\).
• Áp dụng công thức tính thể tích: \({V_{ABCD}} = \dfrac{1}{3}AH.{S_{BCD}}\).

Hướng dẫn giải

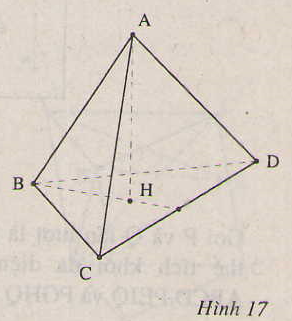
Cho tứ diện đều ABCD.

Hạ đường cao AH của tứ diện thì do các đường xiên AB, AC, AD bằng nhau nên các hình chiếu của chúng: HB, HC, HD bằng nhau. Do BCD là tam giác đều nên H là trọng tâm của tam giác BCD.

Do đó \(BH = \frac{2}{3}.\frac{{\sqrt 3 }}{2}a = \frac{{\sqrt 3 }}{3}a\)

Từ đó suy ra \(A{H^2} = {a^2} - B{H^2}=\)\(\small \frac{6}{9}a^2\)

Nên \(AH = \frac{{\sqrt 6 }}{3}a\)

Thể tích tứ diện đó \(V = \frac{1}{3}.\frac{1}{2}.\frac{{\sqrt 3 }}{2}{a^2}.\frac{{\sqrt 6 }}{3}a = \frac{{{a^3}\sqrt 2 }}{{12}}\).

Tính thể tích khối bát diện đều cạnh a.

Phương pháp giải

• Chia khối bát diện đều thành hai khối chóp tứ giác đều.
• Xác định chiều cao và áp dụng công thức tính thể tích khối chóp: \(V = \dfrac{1}{3}h.{S_d}\)

Hướng dẫn giải

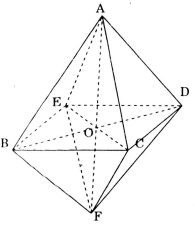
Ta có

\({V_{ABCDEF}} = {V_{ABCDE}} + {V_{FBCDE}} \)

\(= 2{V_{ABCDE}} = 2.\frac{1}{2}{S_{BCDE}}.AO\)

Với O là tâm hình vuông BCDE.

Vì AO vuông góc với mặt phẳng BCDO nên theo định lý Pi-ta-go ta có:

\(AO = \sqrt {A{B^2} - B{O^2}} \)

\(= \sqrt {{a^2} - {{\left( {\frac{{a\sqrt 2 }}{2}} \right)}^2}}  = \frac{a}{{\sqrt 2 }}\)

Vì BCDE là hình vuông cạnh a nên: \({S_{BCDE}} = {a^2}.\)

Do đó: \({V_{ABCDEF}} = \frac{2}{3}{a^2}.\frac{a}{{\sqrt 2 }} = \frac{{{a^3}\sqrt 3 }}{3}.\)

Cho hình hộp ABCD.A’B’C’D’. Tính tỉ số thể tích của khối hộp đó và thể tích của khối tứ diện ACB’D’

Phương pháp giải

• Gọi \(S\) là diện tích đáy \(ABCD\) và \(h\) là chiều cao của khối hộp. Tính thể tích của khối hộp.
• Chia khối hộp thành khối tứ diện \(ACB’D’\) và bốn khối chóp \(A.A’B’D’, C.C’B’D’, B’.BAC\) và \(D’. DAC\). Tính thể tích của bốn khối chóp \(A.A’B’D’, C.C’B’D’, B’.BAC\) và \(D’. DAC\).
• Suy ra \({V_{ACB'D'}} = V - \)\(\left( {{V_{A.A'B'D'}} + {V_{C.C'B'D'}} + {V_{B'BAC}} + {V_{D'.DAC}}} \right)\)
• Tính tỉ số thể tích

Hướng dẫn giải

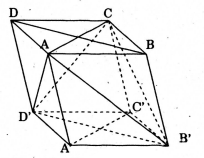
Gọi thể tích khối hộp ABCD.A’B’C’D’ là V

Ta có: \({V_{B'.ABC}} = \frac{1}{3}{V_{ABC.A'B'C'}} = \frac{1}{6}V.\)

\({V_{A.B'D'A'}} = \frac{1}{3}{V_{ABD.A'B'D'}} = \frac{1}{6}V.\)

\({V_{D'.ACD}} = \frac{1}{3}{V_{ACD.A'C'D'}} = \frac{1}{6}V.\)

\({V_{C.B'D'C'}} = \frac{1}{3}{V_{BCD.B'C'D'}} = \frac{1}{6}V.\)

Mặt khác

\(\begin{array}{l}
{V_{C.AD'B'}} = V - ({V_{B'.ABC}} + {V_{A.B'D'A'}}\\
\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + {V_{D'.ACD}} + {V_{C.B'C'D'}})\\
 = V - \frac{4}{6}V = \frac{1}{3}V.
\end{array}\)

Do đó: \(\frac{{{V_{ABCD.A'B'C'D'}}}}{{{V_{ACB'D'}}}} = 3.\)

Cho hình chóp S.ABC. Trên các đoạn thẳng SA, SB, SC lần lượt lấy ba điểm A’, B’, C’ khác với S. Chứng minh rằng: \(\frac{{{V_{S.A'B'C'D'}}}}{{{V_{S.ABC}}}} = \frac{{SA'}}{{SA}}.\frac{{SB'}}{{SB}}.\frac{{SC'}}{{SC}}\)

Phương pháp giải

• Gọi h và h' lần lượt là chiều cao hạ từ A và A' đến \((SBC)\), dựa vào định lí Vi-et tính tỉ số \(\frac{h'}{{h}}\).
• Sử dụng công thức tính diện tích \({S_{\Delta SB'C'}} = \frac{1}{2}SB.SC.\sin \widehat {BSC}\) tính diện tích tam giác \(SB'C'\), tương tự tính diện tích tam giác \(SBC\), sau đó suy ra tỉ số \(\dfrac{{{S_{\Delta SB'C'}}}}{{{S_{\Delta SBC}}}}\).
• Sử dụng công thức tính thể tích \(V = \dfrac{1}{3}S.h\) lập tỉ số thể tích S.A'B'C' và S.ABC, rút gọn và suy ra kết quả.

Hướng dẫn giải

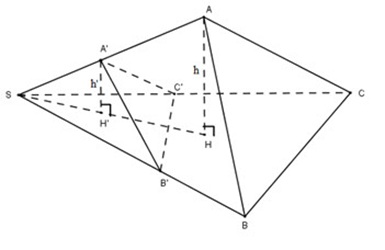
Gọi \(h\) và \(h’\) lần lượt là chiều cao hạ từ \(A, A’\) đến mặt phẳng \((SBC)\).

Do A’H’// AH nên bốn điểm A, A’; H’ và H đồng phẳng. (1)

Lại có, 3 điểm A, S, H đồng phẳng (2).

Từ (1) và (2) suy ra, 5 điểm A, A’, S. H và H’ đồng phẳng.

Trong mp(ASH) ta có: \(\left\{ \begin{array}{l}A'H' \bot SH'\\AH \bot SH\\A'H'//AH\end{array} \right. \Rightarrow SH' \equiv SH\)

⇒ Ba điểm S, H và H’ thẳng hàng.

Gọi \(S_1\) và \(S_2\) theo thứ tự là diện tích các tam giác \(SBC\) và \(SB’C’\).

Khi đó ta có \(\displaystyle{{h'} \over h} = {{SA'} \over {SA}}\) (định lý Ta - let) và:

\(\dfrac{{{S_2}}}{{{S_1}}}=\dfrac{{{S_{SB'C'}}}}{{{S_{SBC}}}} \) \(= \dfrac{{\dfrac{1}{2}SB'.SC'.\sin \widehat {BSC}}}{{\dfrac{1}{2}SB.SC.\sin \widehat {BSC}}} = \dfrac{{SB'}}{{SB}}.\dfrac{{SC'}}{{SC}}\)

Suy ra \(\displaystyle{{{V_{S.A'B'C'}}} \over {{V_{S.ABC}}}} = {{{V_{A'.SB'C'}}} \over {{V_{A.SBC}}}} = {{{1 \over 3}h'{S_2}} \over {{1 \over 3}h{S_1}}}\) \(=\dfrac{{h'}}{h}.\dfrac{{{S_2}}}{{{S_1}}}\) \( = \displaystyle{{SA'} \over {SA}} \cdot {{SB'} \over {SB}} \cdot {{SC'} \over {SC}}\) 

Đó là điều phải chứng minh.

Cho tam giác ABC vuông cân ở A và AB = a. Trên đường thẳng qua C và vuông góc với mặt phẳng (ABC) lấy điểm D sao cho CD = a. Mặt phẳng qua C vuông góc với SD, cắt BD tại F và cắt AD tại E. Tính thể tích khối tứ diện CDEF theo a

Phương pháp giải

• Dựng các điểm F và E.
• Chứng minh tam giác CEF vuông tại E \( \Rightarrow {S_{CEF}} = \dfrac{1}{2}EF.EC\)
• \({V_{CDEF}} = \dfrac{1}{3}DF.{S_{CEF}} \) \(= \dfrac{1}{3}DF.\dfrac{1}{2}EF.EC \) \(= \dfrac{1}{6}DF.EF.EC\)
• Sử dụng định lí Pitago và các hệ thức lượng trong tam giác vuông tính CE, EF và DF.

Hướng dẫn giải

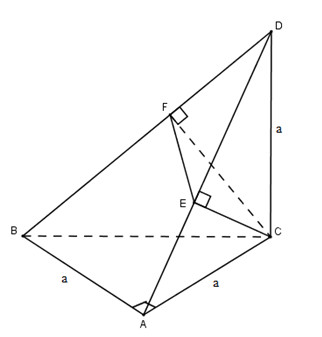
\(\left.\begin{matrix} BA \perp CD& \\ BA \perp CA& \end{matrix}\right\}\)\( \Rightarrow BA\bot (ADC)\) \(\Rightarrow BA \bot CE\)

Mặt khác \(BD \bot (CEF) \Rightarrow BD \bot CE\).

Từ đó suy ra

\(CE \bot (ABD) \Rightarrow CE ⊥ EF, CE \bot AD\).

Vì tam giác \(ACD\) vuông cân, \(AC= CD= a\) nên \(AD = \sqrt {A{C^2} + C{D^2}}  \) \(= \sqrt {{a^2} + {a^2}}  = a\sqrt 2 \)

Suy ra \(CE=\dfrac{AD}{2}=\dfrac{a\sqrt{2}}{2}\)

Ta có \(BC = \sqrt {A{B^2} + A{C^2}}  \) \(= \sqrt {{a^2} + {a^2}}  = a\sqrt 2 \),

\(BD  = \sqrt {B{C^2} + C{D^2}} \) \(= \sqrt{2a^{2}+a^{2}}=a\sqrt{3}\)

Áp dụng hệ thức lượng trong tam giác vuông \(BCD\) ta có: \(CF\cdot BD = DC\cdot BC\) nên \(CF = \frac{{DC.BC}}{{BC}} = \frac{{a.a\sqrt 2 }}{{a\sqrt 3 }} = \frac{{a\sqrt 2 }}{{\sqrt 3 }}\)

Từ đó suy ra 

\(EF= \sqrt{CF^{2}-CE^{2}}\) \(=\sqrt{\dfrac{2}{3}a^{2}-\dfrac{a^{2}}{2}}=\dfrac{\sqrt{6}}{6}a\)

\(DF=\sqrt{DC^{2}-CF^{2}}\) \(=\sqrt{a^{2}-\dfrac{2}{3}a^{2}}=\dfrac{\sqrt{3}}{3}a\)

Từ đó suy ra \(S_{\Delta CEF}=\dfrac{1}{2}FE\cdot EC\) \(=\dfrac{1}{2}\dfrac{a\sqrt{6}}{6}\cdot \dfrac{a\sqrt{2}}{2}=\dfrac{a^{2}\sqrt{3}}{12}\)

Vậy \(V_{D.CEF}=\dfrac{1}{3}S_{\Delta CEF}\cdot DF\) \(=\dfrac{1}{3}\cdot \dfrac{a^{2}\sqrt{3}}{12}\cdot \dfrac{a\sqrt{3}}{3}=\dfrac{a^{3}}{36}.\)

Cho hai đường thẳng chéo nhau d và d’. Đoạn thằng AB có độ dài a trượt trên d, đoạn thẳng CD có độ dài B trượt trên d’. Chứng minh rằng khối tứ diện ABCD có thể tích không đổi.

Hướng dẫn giải

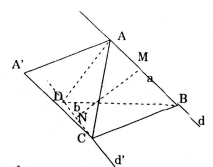
Gọi khoảng cách giữa 2 đường thẳng chéo nhau d, d' và góc của d và d' là \(\varphi .\)

Trong mặt phẳng (ABC) dựng hình bình hành CBAA'.

Ta có AA'//BC nên \({V_{ABCD}} = {V_{A'BCD}}\)

Gọi MN là đoạn vuông góc chung của AB và CD \(\left( {M \in AB,\,\,N \in CD} \right)\)

Vì BM//CA' nên \({V_{BA'CD}} = {V_{MA'CD}}\)

Ta có \(MN \bot AB\) nên \(MN \bot CA',\) hơn nữa \(MN \bot CD.\)

Do đó \(MN \bot (CDA')\)

Chú ý rằng: \(\widehat {\left( {AB,CD} \right)} = \widehat {\left( {AC',CD} \right)} = \varphi \)

Nên \({V_{M.A'CD}} = \frac{1}{3}.{S_{A'CD}}.MN \)

\(=\frac{1}{3}.\frac{1}{2}.CA'.CD.\sin \varphi .MN \)

\(= \frac{1}{6}a.b.h.\sin \varphi \)

\( \Rightarrow {V_{ABCD}} = \frac{1}{6}a.b.h.\sin \varphi .\)