Giải bài tập SGK Toán 12 Bài 1: Khái niệm về khối đa diện
Phần hướng dẫn giải bài tập khái niệm về khối đa diện sẽ giúp các em nắm được phương pháp và rèn luyện kĩ năng các giải bài tập từ SGK Hình học 12 Cơ bản và Nâng cao.
Mục lục nội dung

1. Giải bài 1 trang 12 SGK Hình học 12
Chứng minh rằng một đa diện có các mặt là những tam giác thì tổng số các mặt của nó phải là một số chẵn. Cho ví dụ
Hướng dẫn giải
Gọi số các mặt của đa diện là n \((n\in \mathbb{Z},n\geq 4)\). Vì mỗi mặt của khối đa diện có 3 cạnh và mỗi cạnh chỉ là cạnh chung của đúng hai mặt nên số cạnh của nó là: \(\frac{3n}{2}\)
Vì số cạnh phải là số tự nhiên, nên ta có 3n chia hết cho 2, từ đây ta suy ra r chia hết cho 2.
Ví dụ: Hình tứ diện có 4 mặt
2. Giải bài 2 trang 12 SGK Hình học 12
Chứng minh rằng một đa diện mà mỗi đỉnh của nó đều là đỉnh chung của số lẻ mặt thì tổng số các đỉnh của nó là một số chẵn. Cho ví dụ.
Hướng dẫn giải
Giả sử tổng số đỉnh của khối đa diện là n \((n\geq 4, n\in \mathbb{N}*)\) và các đỉnh là: A1, A2, A3,..,An. Gọi số mặt của đa diện chứa đỉnh Ai là 2mi +1 ⇒ số cạnh Ai là 2mi + 1. Vì mỗi cạnh là cạnh chung của đúng hai mặt nên số cạnh của khối đa diện là:
\(\begin{array}{l}
c = \frac{{2{m_1} + 1 + 2{m_2} + 1 + ... + 2{m_n} + 1}}{2}\\
\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( {i = \overline {1,n} ;m \in {N^*}} \right)
\end{array}\)
\(=\frac{2(m_1+m_2+...+m_n)+n}{2}\)
\(=m_1+m_2+...+m_n+\frac{n}{2}\)
Vì c nguyên, nên \(\frac{n}{2}\) nguyên hay n là số chẵn.
3. Giải bài 3 trang 12 SGK Hình học 12
Chia một khối lập phương thành năm khối tứ diện.
Hướng dẫn giải
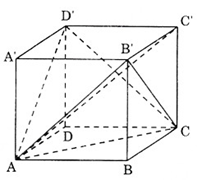
Chia khối lập phương ABCD.A'B'C'D' thành năm khối tứ diện như sau: A'B'CD', A'AB'D', BACB', C'B'CD', DACD'.
4. Giải bài 4 trang 12 SGK Hình học 12
Chia một khối lập phương thành sáu khối tứ diện bằng nhau.
Hướng dẫn giải
Chia lăng trụ ABD.A'B'D' thành ba tứ diện DABD', A'ABD', A'B'BD'. Phép đối xứng qua (ABD') biến DABD' thành A'ABD', Phép đối xứng qua (BA'D') biến A'ABD' thành A'B'BD' nên ba tứ diện DABA', A'ABD', A'B'BD' bằng nhau
Làm tương tự đối với lăng trụ BCD.B'C'D' ta sẽ chia được hình lập phương thành sáu tứ diện bằng nhau.