Giải bài tập SGK Toán 11 Nâng cao Bài 3: Phép đối xứng trục

Qua phép đối xứng trục D_a (a là trục đối xứng), đường thẳng d biến thành đường thẳng d′. Hãy trả lời các câu hỏi sau:

a) Khi nào thì d song song với d′?

b) Khi nào thì d trùng với d′?

c) Khi nào thì d cắt d′? Giao điểm của d và d′có tính chất gì?

Phương pháp giải:

Từ vị trí tương đối của d và d' suy ra vị trí của a và kết luận.

Hướng dẫn giải:

a) Khi d // a thì d // d’.

b) Khi d vuông góc với a hoặc d trùng với a thì d trùng với d’.

c) Khi góc giữa d và a bằng 45^o thì d ⊥ d′.

Trong mặt phẳng tọa độ Oxy, cho các đường tròn (C₁) và (C₂) lần lượt có phương trình:

\(\eqalign{ & \left( {{C_1}} \right):{x^2} + {y^2} - 4x + 5y + 1 = 0 \cr & \left( {{C_2}} \right):{x^2} + {y^2} + 10y - 5 = 0 \cr}\)

Viết phương trình ảnh của mỗi đường tròn trên qua phép đối xứng có trục Oy

Phương pháp giải:

- Tìm tâm I, bán kính R của đường tròn.

- Tìm ảnh I' của tâm qua phép đối xứng trục Oy.

- Ảnh của đường tròn có tâm I', bán kính R.

Hướng dẫn giải:

Ta có:

\(\eqalign{ & {x^2} + {y^2} - 4x + 5y + 1 = 0 \cr & \Leftrightarrow {\left( {x - 2} \right)^2} + {\left( {y + {5 \over 2}} \right)^2} = {{37} \over 4} \cr} \)

(C₁) có tâm \({I_1}\left( {2; - {5 \over 2}} \right)\) và bán kính \({R_1} = {{\sqrt {37} } \over 2}\)

Gọi \(I'_1\) là ảnh của \(I_1\) qua phép đối xứng có trục Oy thì \(I{'_1}\left( { - 2; - {5 \over 2}} \right)\)

Vậy phương trình ảnh \((C'_1)\) của \((C_1)\) qua phép đối xứng trục Oy là:

\(\eqalign{ & {\left( {x + 2} \right)^2} + \left( {y + {5 \over 2}} \right) = {{37} \over 4} \cr & \Leftrightarrow {x^2} + {y^2} + 4x + 5y + 1 = 0 \cr} \)

Lại có:

\(\begin{array}{l} \left( {{C_2}} \right):{x^2} + {y^2} + 10y - 5 = 0\\ \Leftrightarrow {x^2} + {\left( {y + 5} \right)^2} = 30 \end{array}\)

\((C_2)\) có tâm \({I_2}\left( {0;-5} \right)\) và bán kính \({R_2} = \sqrt {30}\)

Gọi \(I'_2\) là ảnh của \(I_2\) qua phép đối xứng có trục Oy thì \(I{'_2}\left( { 0; - 5} \right)\) trùng với \(I_2\)

Vậy phương trình ảnh \((C'_2)\) của \((C_2)\) qua phép đối xứng trục Oy là chính \(\left( {{C_2}} \right):{x^2} + {y^2} + 10y - 5 = 0\)

Cho góc nhọn xOy và một điểm A nằm trong góc đó. Hãy xác định điểm B trên Ox và điểm C trên Oy sao cho tam giác ABC có chu vi nhỏ nhất

Hướng dẫn giải:

- Gọi A’ và A” là các điểm đối xứng với điểm A lần lượt qua các đường thẳng Ox và Oy.

- Dùng bất đẳng thức tam giác chứng minh chu vi tam giác ABC lớn hơn hoặc bằng AA'.

Phương pháp giải:

Xét tam giác bất kì ABC có B và C lần lượt nằm trên hai tia Ox và Oy.

Gọi A’ và A” là các điểm đối xứng với điểm A lần lượt qua các đường thẳng Ox và Oy.

Ta có AB = A′B và AC = A”C ( do các \(△ABA’\) và \(△ACA”\) là các tam giác cân).

Gọi 2p là chu vi của tam giác ABC thì: 2p = AB + BC + CA = A′B + BC + CA” ≥ A′A”

Dấu “=” xảy ra khi bốn điểm A′, B, C, A” thẳng hàng.

Suy ra để chu vi tam giác ABC bé nhất thì phải lấy B và C lần lượt là giao điểm của đoạn thẳng A’A” với hai tia Ox và Oy (các giao điểm đó tồn tại vì góc xOy nhọn).

Cho hai điểm B,C cố định nằm trên đường tròn và điểm A thay đổi trên đường tròn đó. Hãy dùng phép đối xứng trục để chứng minh rằng trực tâm H của tam giác ABC nằm trên một đường tròn cố định

Hướng dẫn: Khi BC không phải là đường kính, gọi H' là giao điểm của đường thẳng AH với đường tròn. Chứng minh rằng đối xứng với qua đường thẳng BC.

Phương pháp giải:

Khi BC không phải là đường kính, gọi H' là giao điểm của đường thẳng AH với đường tròn.

Chứng minh rằng đối xứng với qua đường thẳng BC

Hướng dẫn giải:

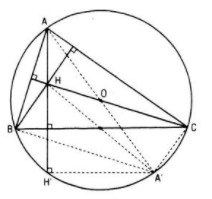
Trường hợp BC là đường kính thì H trùng A, do đó H nằm trên đường tròn cố định (O ; R)

Xét trường hợp BC không là đường kính.

Giả sử đường thẳng AH cắt đường tròn (O ; R) tại H’. Như vậy với mỗi điểm A ∈ (O ; R), khác với B và C thì ta xác định điểm H’ ∈ (O ; R).

Gọi AA’ là đường kính của đường tròn (O ; R)

⇒ A’B // CH (vì cùng vuông góc với AB) và A’C // BH (vì cùng vuông góc với AC)

⇒ A’BHC là hình bình hành.

Vậy BC đi qua trung điểm của HA’

Mặt khác BC // A’H’ (vì cùng vuông góc với AH) nên BC cũng đi qua trung điểm của HH’, do đó H và H’ đối xứng với nhau qua BC

Nếu gọi Đ là phép đối xứng có trục là đường thẳng BC thì Đ biến H’ thành H.

Nhưng H’ luôn luôn nằm trên (O ; R) nên H nằm trên đường tròn cố định là ảnh của đường tròn (O ; R) qua phép đối xứng trục Đ

a) Chỉ ra trục đối xứng (nếu có) của mỗi hình sau đây (mỗi hình là một từ bao gồm một số chữ cái):

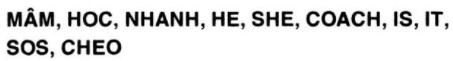
b) Chứng minh rằng đồ thị của hàm số chẵn luôn có trục đối xứng

Phương pháp giải:

a) Tìm hình có trục đối xứng và xác định trục của nó.

b) - Lấy điểm M(x ; y) thuộc đồ thị hàm số chẵn y = f(x).

- Tìm M' là điểm đối xứng của M qua Oy.

- Chứng minh M' thuộc đồ thị hàm số y = f(x).

Hướng dẫn giải:

a) Các hình có trục đối xứng là:

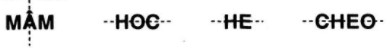
b) Ta sẽ chứng minh: Trục Oy luôn là trục đối xứng của đồ thị hàm số chẵn y = f(x).

Lấy điểm M(x ; y) thuộc đồ thị. Gọi M' là điểm đối xứng của M qua Oy thì M'(-x;y).

Ta kiểm tra M'(-x;y) thuộc đồ thị hàm số y = f(x).

Do hàm số y = f(x) là chẵn nên f(-x) = f(x) = y hay f(-x) = y hay M'(-x;y) thuộc đồ thị hàm số y = f(x).

Vậy trục Oy là trục đối xứng của đồ thị hàm số chẵn.