Giải bài tập SGK Toán 11 Bài 2: Phép tịnh tiến
eLib xin chia sẻ với các em học sinh lớp 11 nội dung giải bài tập SGK bài Phép tịnh tiến bên dưới đây. Với nội dung đầy đủ 4 bài tập trang 7, 8 đi kèm đó là phương pháp và hướng dẫn giải chi tiết, hi vọng rằng đây sẽ là tài liệu giúp các em học tập tốt hơn. Sau đây mời các em cùng tham khảo.
Mục lục nội dung

1. Giải bài 1 trang 7 SGK Hình học 11
Chứng minh rằng: \(M'=T_{\vec{v}}(M) \Leftrightarrow M = (M')\)
Phương pháp giải
Sử dụng định nghĩa của phép tịnh tiến: \({T_{\overrightarrow v }}\left( M \right) = M' \Leftrightarrow \overrightarrow {MM'} = \overrightarrow v \)
Hướng dẫn giải
Ta có: \(M'=T_\vec{v}(M)\Leftrightarrow \overrightarrow{MM'}= \overrightarrow{v}\Leftrightarrow \overrightarrow{M'M}=-\overrightarrow{v}\)
\(\Leftrightarrow M=T_{-\vec{v}}.(M')\) (đpcm).
2. Giải bài 2 trang 7 SGK Hình học 11
Cho tam giác ABC có G là trọng tâm. Xác định ảnh của tam giác ABC qua phép tịnh tiến theo vectơ \(\overrightarrow{AG}.\) Xác định điểm D sao cho phép tịnh tiến theo vectơ \(\overrightarrow{AG}\) biến D thành A.
Phương pháp giải
Sử dụng định nghĩa của phép tịnh tiến: \({T_{\overrightarrow v }}\left( M \right) = M' \Leftrightarrow \overrightarrow {MM'} = \overrightarrow v \)
Hướng dẫn giải
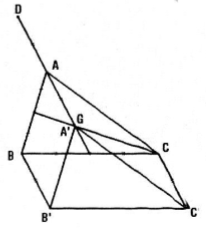
Gọi A' là hình ảnh của A qua phép tịnh tiến theo vectơ \(\overrightarrow{AG}\) ta có \(T_{\overrightarrow{AG}}(A)=A'\Leftrightarrow \overrightarrow{AA'}=\overrightarrow{AG} \Leftrightarrow A'=G\)
Tương tự: \(B'=T_{\overrightarrow{AG}}(B)\Leftrightarrow \overrightarrow{BB'}=\overrightarrow{AG}\) hay B' là đỉnh thứ tư của hình bình hành ABB'G.
\(C'=T_{\overrightarrow{AG}}(C)\Leftrightarrow \overrightarrow{CC'}=\overrightarrow{AG}\) hay C' là đỉnh thứ tư của hình bình hành ACC'G.
Vậy \(\Delta A'B'C'\) là ảnh của \(\Delta ABC\) đã dựng được.
Ta có: \(T_{\overrightarrow{AG}}(D)=A\Leftrightarrow \overrightarrow{DA}=\overrightarrow{AG}\) hay D là điểm nằm trên đường thẳng đi qua AG và AD = AG.
3. Giải bài 3 trang 7 SGK Hình học 11
Trong mặt phẳng tọa độ Oxy cho vectơ \(\vec v = ( -1;2),\) hai điểm \(A(3;5), B( -1; 1)\) và đường thẳng d có phương trình \(x-2y+3=0\).
a) Tìm tọa độ của các điểm A', B' theo thứ tự là ảnh của A, B qua phép tịnh tiến theo \(\overrightarrow v \)
b) Tìm tọa độ của điểm C sao cho A là ảnh của C qua phép tịnh tiến theo \(\overrightarrow v \)
c) Tìm phương trình của đường thẳng d' là ảnh của d qua phép tịnh tiến theo \(\overrightarrow v \)
Phương pháp giải
Sử dụng biểu thức tọa độ của phép tịnh tiến: Phép tịnh tiến theo vector \(\overrightarrow v \left( {a;b} \right)\) biến điểm M(x;y) thành điểm M'(x';y'). Khi đó \(\overrightarrow {MM'} = \overrightarrow v \Leftrightarrow \left\{ \matrix{x' - x = a \hfill \cr y' - y = b \hfill \cr} \right. \) \(\Leftrightarrow \left\{ \matrix{x' = x + a \hfill \cr y' = y + b \hfill \cr} \right.\)
Hướng dẫn giải
Biểu thức toạ độ của phép tịnh tiến \(T_{\overrightarrow v}\) là \(\left\{\begin{matrix} x' =x-1\\ y'=x+2 \end{matrix}\right.\)
Câu a: Gọi A(xA; yA); B(xB; yB) ta có
\(\left\{\begin{matrix} x_A'=x_A -1\\ y_A'=y_A+2 \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x_A'=3-1=2\\ y_A'=5+2=7 \end{matrix}\right.\) hay A'(2;7).
\(\left\{\begin{matrix} x_B'=x_A -1\\ y_B'=y_A+2 \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x_B'=-2\\ y_B'=3 \end{matrix}\right.\) hay B'(-2;3).
Câu b: A là ảnh của C qua \(T_{\overrightarrow v}\) thì ta có: \(\left\{\begin{matrix} x_A=x_C-1\\ y_A=y_C+2 \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x_C=x_A+1\\ y_C=y_A-2 \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x_C=4\\ y_C=3 \end{matrix}\right.\) hay C(4; 3)
Câu c: Gọi \(M(x;y) \in d\)
\(M'(x';y') \in d'\) là ảnh của M qua phép tịnh tiến theo vectơ.
Ta có: \(\overrightarrow {MM'} = \overrightarrow v \Rightarrow \left\{ \begin{array}{l}x' = x - 1\\y' = y + 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = x' + 1\\y = y' - 2\end{array} \right.\)
Thay vào phương trình đường thẳng d ta có:
\((x' + 1) - 2(y' - 2) + 3 = 0 \Leftrightarrow x' - 2y' + 8 = 0\)
Vậy phương trình của d’ là: \(x - 2y + 8 = 0.\)
4. Giải bài 4 trang 8 SGK Hình học 11
Cho hai đường thẳng a và b song song với nhau. Hãy chỉ ra một phép tịnh tiến biến a thành b. Có bao nhiêu phép tịnh tiến như thế?
Phương pháp giải
Áp dụng tính chất của phép tịnh tiến: Phép tịnh tiến biến một đường thẳng thành một đường thẳng song song với đường thẳng ban đầu.
Hướng dẫn giải
Phép tịnh tiến \({T_{\overrightarrow v }}\) với vectơ \(\overrightarrow{v}\) bất kì khác với các vecto chỉ phương của a và b điều biến a thành b.
Vậy có vô số phép tịnh tiến như trên.



