Giải bài tập SGK Toán 12 Ôn tập chương 3: Nguyên hàm. Tích phân và Ứng dụng
Hướng dẫn Giải bài tập Nguyên hàm, Tích phân và Ứng dụng sẽ giúp các em học sinh nắm vững phương pháp giải bài tập và ôn luyện tốt kiến thức đã học.
Mục lục nội dung
1.1. Giải bài 1 trang 126 SGK Giải tích 12
1.2. Giải bài 2 trang 126 SGK Giải tích 12
1.3. Giải bài 3 trang 126 SGK Giải tích 12
1.4. Giải bài 4 trang 126 SGK Giải tích 12
1.5. Giải bài 5 trang 127 SGK Giải tích 12
1.6. Giải bài 6 trang 127 SGK Giải tích 12
1.7. Giải bài 7 trang 127 SGK Giải tích 12
2.1. Giải bài 1 trang 127 SGK Giải tích 12
2.2. Giải bài 2 trang 128 SGK Giải tích 12
2.3. Giải bài 3 trang 128 SGK Giải tích 12
2.4. Giải bài 4 trang 128 SGK Giải tích 12

1. Bài tập tự luận
1.1. Giải bài 1 trang 126 SGK Giải tích 12
a) Phát biểu định nghĩa nguyên hàm của hàm số f(x) trên một khoảng
b) Nêu phương pháp tính nguyên hàm từng phần. Cho ví dụ minh họa
Hướng dẫn giải
Câu a: Định nghĩa
Cho hàm số \(f(x)\) xác định trên K.
Hàm số \(F(x)\) được gọi là nguyên hàm của hàm số \(f(x)\) trên K nếu \(F'(x) = f(x)\) với mọi \(x \in K.\)
- Nếu \(F(x)\) là một nguyên hàm của hàm số \(f(x)\) trên K thì với mỗi hằng số C, hàm số \(G(x) = F(x)+C\) cũng là một nguyên hàm của hàm số \(f(x)\) trên K.
- Nếu \(F(x)\) là một nguyên hàm của hàm số \(f(x)\) trên K thì mọi nguyên hàm của \(f(x)\) trên K đều có dạng \(F(x)+C\) với \(C\) là một hằng số tùy ý.
- Kí hiệu họ nguyên hàm của hàm số \(f(x)\) là \(\int f(x)dx\). Khi đó : \(\int f(x)dx=F(x)+C,C\in \mathbb{R}.\)
Câu b: Phương pháp tính nguyên hàm từng phần
Định lí: Nếu hai hàm số \(u=u(x)\) và \(v=v(x)\) có đạo hàm và liên tục trên K thì: \(\int {u(x)v'(x)dx} = u(x)v(x) - \int {u'(x)v(x)dx}\)
Một số dạng thường gặp:
Dạng 1: \(\int {P(x).{e^{{\rm{ax}} + b}}dx\,,\,\,\int {P(x)\sin ({\rm{ax}} + b)dx\,,\,\int {P(x)c{\rm{os}}({\rm{ax}} + b)dx} } }\)
Cách giải: Đặt \(u = P(x)\,,\,dv = {e^{{\rm{ax}} + b}}dx\,\)
Hoặc \(dv = \sin (ax + b)dx,\,\,dv = \cos (ax + b)dx.\)
Dạng 2: \(\int {P(x)\ln ({\rm{ax}} + b)dx}\)
Cách giải: Đặt \(u = \ln ({\rm{ax}} + b)\,,\,dv = P(x)dx.\)
Ví dụ minh họa
Giải phương trình \(I = \int {x{\rm{sin2}}xdx}\)
Giải
Đặt \(\left\{ \begin{array}{l} u = x\\ dv = \sin 2xdx \end{array} \right. \Rightarrow \left\{ \begin{array}{l} du = dx\\ v = - \frac{1}{2}\cos 2x \end{array} \right.\)
\(\Rightarrow I = - \frac{1}{2}x\cos 2x + \frac{1}{2}\int {\cos 2xdx} = - \frac{1}{2}x\cos 2x + \frac{1}{4}\sin 2x + C\)
1.2. Giải bài 2 trang 126 SGK Giải tích 12
a) Phát biểu định nghĩa tích phân của hàm số f(x) trên một đoạn
b) Nêu các tính chất của tích phân. Cho ví dụ minh họa
Hướng dẫn giải
Câu a: Định nghĩa tích phân của hàm số f(x) trên một đoạn
Định nghĩa: Cho hàm \(f(x)\) liên tục trên khoảng K và a, b là hai số bất kỳ thuộc K. Nếu \(F(x)\) là một nguyên hàm của \(f(x)\) thì hiệu số \(F(b)-F(a)\) được gọi là tích phân của \(f(x)\) từ a đến b và ký hiệu là \(\int\limits_a^b {f(x)dx} .\) Trong trường hợp \(a
Câu b: Các tính chất của tích phân và ví dụ minh họa
Các tính chất của tích phân:
Cho các hàm số \(f(x),\,g(x)\) liên tục trên K và \(a,b,c\) là ba số thuộc K.
- \(\,\int\limits_a^a {f(x)dx = 0}\)
- \(\int\limits_a^b {f(x)dx = - \int\limits_b^a {f(x)dx} }\)
- \(\int\limits_a^b {f(x)dx = \int\limits_a^c {f(x)dx} + \int\limits_c^b {f(x)dx} }\)
- \(\int\limits_a^b {k.f(x)dx = k\int\limits_a^b {f(x)dx} }\)
- \(\int\limits_a^b {[f(x) \pm g(x)]dx = \int\limits_a^b {f(x)dx} \pm \int\limits_a^b {g(x)dx} }\)
Ví dụ minh họa
Tính tích phân: \(I = \int\limits_1^2 {\frac{{{x^2} - 2x}}{{{x^3}}}dx}\)
Giải
\(I = \int\limits_1^2 {\frac{{{x^2} - 2x}}{{{x^3}}}dx} = \int\limits_1^2 {\left( {\frac{1}{x} - \frac{2}{{{x^2}}}} \right)dx} = \left. {\left( {\ln \left| x \right| + \frac{2}{x}} \right)} \right|_1^2\)
\(= \left( {\ln 2 + 1} \right) - \left( {\ln 1 + 2} \right) = - 1 + \ln 2\)
1.3. Giải bài 3 trang 126 SGK Giải tích 12
Tìm nguyên hàm của các hàm số sau
a) \(f(x)=(x-1)(1-2x)(1-3x)\)
b) \(f(x)=sin4xcos^22x\)
c) \(f(x)=\frac{1}{1-x^2}\)
d) \(f(x)=(e^x-1)^3\)
Phương pháp giải
Biến đổi hàm số cần tính nguyên hàm về tổng của các hàm số mà ta đã biết công thức xác định nguyên hàm của chúng đã được học ở bài 1 chương 3 Giải tích 12.
Hướng dẫn giải
Câu a
Ta có \(f(x)=(x-1)(6x^2-5x+1)=x^3-11x^2+6x-1\)
Vậy \(\int f(x)dx=\frac{3x^4}{2}-\frac{11}{3}x^3+3x^2-C\).
Câu b
Ta có \(\sin 4x.co{s^2}2x = \sin 4x.\frac{1}{2}(1 + \cos 4x)\)
Vậy \(\begin{array}{l} \int {f(x)dx} = \frac{1}{2}\int {\sin 4xdx} + \frac{1}{4}\int {\sin 8xdx} \\ = - \frac{1}{8}\cos 4x - \frac{1}{{32}}\cos 8x + C. \end{array}\)
Câu c
Ta có
\(\begin{array}{l} f(x)\frac{1}{{1 - {x^2}}} = \frac{1}{{(1 - x)(1 + x)}} = \frac{a}{{1 - x}} + \frac{b}{{1 + x}}\\ = \frac{{a(1 + x) + b(1 - x)}}{{(1 - x)(1 + x)}} = \frac{{(a - b)x + a + b}}{{(1 - x)(1 + x)}}\\ \Leftrightarrow \left\{ \begin{array}{l} a - b = 0\\ a + b = 1 \end{array} \right. \Rightarrow f(x) = \frac{1}{2}\left[ {\frac{1}{{1 - x}} + \frac{1}{{1 + x}}} \right] \end{array}\)
Vậy \(f(x)dx=\frac{1}{2}\int \frac{1}{1+x}dx-\frac{1}{2}\int \frac{1}{x-1}dx\) \(=\frac{1}{2}ln\left | x+1 \right |-\frac{1}{2}ln\left | x-1 \right |= \frac{1}{2}ln \left | \frac{x+1}{x-1} \right |+C\).
Câu d
Ta có: \(\int (e^x-1)^3dx=\int (e^{3x}-3e^{2x}+3e^x-1)dx\) \(=\frac{1}{3}e^{3x}-\frac{3}{2}e^{2x}+3e^x-x+C\).
1.4. Giải bài 4 trang 126 SGK Giải tích 12
Tính
a) \(\int (2-x)sinxdx\)
b) \(\frac{\int (x+1)^2}{\sqrt{x}}dx\)
c) \(\int \frac{e^{3x+1}}{e^x+1}dx\)
d) \(\int \frac{1}{(sinx+cosx)^2}dx\)
e) \(\int \frac{1}{\sqrt{1+x}+\sqrt{x}}dx\)
f) \(\int \frac{1}{(1+x)(2-x)}dx\)
Phương pháp giải
Sử dụng các công thức nguyên hàm cơ bản và các phương pháp tính nguyên hàm để làm bài toán.
Hướng dẫn giải
Câu a
Đặt \(\left\{\begin{matrix} u=2-x\\ dv=sinx dx \end{matrix}\right.\Rightarrow \left\{\begin{matrix} du=-dx\\ v=-cosx \end{matrix}\right.\)
Áp dụng cộng thức tính nguyên hàm từng phần ta có:
\(\int (2-x)sinx dx=-(2-x)cosx-\int cosx dx\)
\(=(x-2)cosx-sinx+C\)
Câu b
\(\int \frac{(x+1)^2}{\sqrt{x}}=\frac{x^2+2x+1}{x^{\frac{1}{2}}}dx\)
\(=\int \left ( x^\frac{3}{2}+2x^{\frac{1}{2}}+x^{-\frac{1}{2}} \right )dx\)
\(=\int x^{\frac{3}{2}}dx+2\int x^{\frac{1}{2}}dx+\int x^{-\frac{1}{2}}dx\)
\(=\frac{1}{1+\frac{3}{2}}x^{\frac{3}{2}+1}+\frac{2}{1 +\frac{1}{2}}x^{\frac{1}{2}+1}+\frac{1}{1-\frac{1}{2}}x^{-\frac{1}{2}+1}+C\)
\(=\frac{2}{5}x^\frac{5}{2}+ \frac{4}{3}x^{\frac{3}{2}}+2x^{\frac{1}{2}}+C.\)
Câu c
\(\int \frac{e^{3x}+1}{e^x+1}dx=\int (e^{2x}-e^x+1)dx=\int e^{2x}dx- \int e^x dx +\int dx\)
\(=\frac{1}{2}\int e^{2x}d(2x)-\int e^xdx+\int dx=\frac{1}{2}e^{2x}-e^x+x+C\)
Câu d
\(\int \frac{1}{(sinx+cosx)^2}dx=\frac{1}{2}\int \frac{dx}{cos^2(x-\frac{\pi }{4})} =\frac{1}{2} tan \left ( x-\frac{\pi }{4} \right )+C\)
Câu e
\(\int \frac{1}{\sqrt{1+x}+\sqrt{x}}dx=\int \frac{\sqrt{1+x}-\sqrt{x}}{1+x-x}dx\)
\(=\int (\sqrt{1+x}-\sqrt{x})dx=\int \sqrt{1+x}dx-\int \sqrt{x}dx\)
\(=\int (1+x)^{\frac{1}{2}}d(1+x)-\int x^{\frac{1}{2}}dx\)
\(=\frac{2}{3}(1+x)^\frac{3}{2}-\frac{2}{3}x^{\frac{3}{2}}+C\)
Câu f
\(\int \frac{1}{(1+x)(2-x)}dx=\frac{1}{3}\int \left ( \frac{1}{1+x}+ \frac{1}{2-x} \right )dx\)
\(=\frac{1}{3}\left ( \int \frac{dx}{1+x}+ \int \frac{dx}{2-x} \right )= \frac{1}{3}\left ( \int \frac{d(1+x)}{1+x} - \int \frac{d(2-x)}{2-x}\right )\)
\(=\frac{1}{3}\left ( ln \left | 1+x \right | - ln\left | 2-x \right | \right )+C =\frac{1}{3}ln \left | \frac{1+x}{2-x} \right |+C\)
1.5. Giải bài 5 trang 127 SGK Giải tích 12
Tính
a) \(\int_{3}^{0}\frac{x}{\sqrt{1+x}}dx\)
b) \(\int_{1}^{64} \frac{1+\sqrt{x}}{\sqrt[3]{x}}dx\)
c) \(\int_{0}^{2} x^2.e^{3x}dx\)
d) \(\int_{0}^{\pi} \sqrt{1+sin2x}dx\)
Phương pháp giải
- Sử dụng phương pháp đổi biến và các công thức tính tích phân cơ bản để tính tích phân.
- Chú ý: Khi đổi biến cần đổi cận.
Hướng dẫn giải
Câu a
\(\int_{0}^{3}\frac{x}{\sqrt{1+x}}dx=\int_{0}^{3}\frac{x+1-1}{\sqrt{1+x}}dx\)
\(=\int_{0}^{3}\frac{x+1}{\sqrt{1+x}}dx-\int_{0}^{3}\frac{dx}{\sqrt{1+x}}\)
\(=\int_{0}^{3}(x+1)^{\frac{1}{2}}dx-\int_{0}^{3}(1+x)^{\frac{1}{2}}dx\)
\(= \int_{0}^{3}(x+1)^{\frac{1}{2}}d(x+1)-\int_{0}^{3}(1+x)^{\frac{1}{2}}d(1+x)\)
\(=\frac{2}{3}(x+1)^\frac{3}{2} \Bigg |^3_0-2(1+x)^{\frac{1}{2}}\Bigg |^3_0= \frac{2}{3}-2.4^\frac{1}{2}+2\)
\(=\frac{16}{3}-\frac{2}{3}-4+2=\frac{14}{3}-2=\frac{8}{3}\)
Câu b
Đặt \(t=\sqrt[6]{x}\Rightarrow x=t^6\Rightarrow dx=6t^5 dt.\)
Khi x = 1 ⇒ t = 1
Khi x = 64 ⇒ t = 2
Do đó ta có: \(I=\int_{1}^{64}\frac{1+\sqrt{x}}{\sqrt[3]{x}}dx= \int_{1}^{2}\frac{1+t^3}{t^2}.6t^5dt =\int_{1}^{2}(6t^3+6t^6)dt\)
\(=\left [ \frac{3t^4}{2} +\frac{6t^7}{7} \right ] \Bigg |^2_1= \frac{3(16-1)}{2}+\frac{6(128-1)}{7}=\frac{1839}{14}.\)
Câu c
Sử dụng phương pháp tính tích phân từng phần bằng cách đặt:
\(\left\{\begin{matrix} u=x^2\\ dv=e^{3x}dx \end{matrix}\right.\Rightarrow \left\{\begin{matrix} du=2x dx\\ v=\frac{1}{3}e^{3x} \end{matrix}\right.\)
Ta có
\(\int_{0}^{2}x^2 e^{3x}dx=\frac{1}{3}x^3.e^{3x} \bigg|_0^2-\frac{2}{3} \int_{0}^{2}x.e^{3x}dx=\frac{4}{3}e^6-\frac{2}{3}\int_{0}^{2}x.e^{3x}dx\)
Lại tiếp tục đặt: \(\left\{\begin{matrix} u_1=x^2\\ dv_1=e^{3x}dx \end{matrix}\right.\Rightarrow \left\{\begin{matrix} du_1=dx\\ v_1=\frac{1}{3}e^{3x} \end{matrix}\right.\)
Ta được
\(\int_{0}^{2}x.e^{3x}dx=\frac{1}{3}x.e^{3x} \bigg|^2_0-\frac{1}{3} \int_{0}^{2}e^{3x}dx\)
\(=\frac{2}{3}e^6-\frac{1}{9}e^{3x}\bigg|_{0}^{2}=\frac{2}{3}e^6-\frac{1}{9}e^6+ \frac{1}{9}\)
Do đó: \(\int_{0}^{2}x^2.e^{3x}dx=\frac{4}{3}e^6-\frac{2}{3} \left ( \frac{2}{3}e^6-\frac{1}{9}e^6+\frac{1}{9} \right )\)
\(=\frac{4}{3}e^6-\frac{4}{9}e^6+\frac{2}{27}e^6-\frac{2}{27}= \frac{26}{27}e^6-\frac{2}{27}=\frac{2}{27}(13e^6-1)\)
Câu d
Ta có
\(\sqrt{1+sin2x}=\sqrt{(sinx+cosx)^2}= \sqrt{2cos^2(x-\frac{\pi }{4})}\)
\(= \sqrt{2}\left | cos\left ( x-\frac{\pi }{4} \right ) \right |\)
Mặt khác ta có
\(cos\left ( x-\frac{\pi }{4} \right )\geq 0, \ \ \ \forall x\in \left [ 0;\frac{3\pi }{4} \right ]\)
và \(cos\left ( x-\frac{\pi }{4} \right )\leq 0, \ \ \ \forall x\in \left [\frac{3\pi }{4}; \pi \right ]\)
Do đó
\(\int_{0}^{\pi }\sqrt{1+sin2x}dx=\sqrt{2}\int_{0}^{\pi }cos \left ( x-\frac{\pi }{4} \right ) \bigg| dx\)
\(=\sqrt{2}\int_{0}^{\frac{3\pi }{4}}cos\left ( x-\frac{\pi }{4} \right )dx- \sqrt{2}\int^{0}_{\frac{3\pi }{4}}cos\left ( x-\frac{\pi }{4} \right )dx\)
\(=\sqrt{2}sin\left ( x-\frac{\pi }{4} \right ) \Bigg|_0^{\frac{3\pi }{4}}- \sqrt{2}sin\left ( x-\frac{\pi }{4} \right )\Bigg|^0_{\frac{3\pi }{4}}\)
\(=\sqrt{2}\left ( 1+\frac{\sqrt{2}}{2} \right )-\sqrt{2} \left ( \frac{\sqrt{2}}{2} -1\right )= \sqrt{2}+\sqrt{2}=2\sqrt{2}\)
1.6. Giải bài 6 trang 127 SGK Giải tích 12
Tính
a) \(\int_{0}^{\frac{\pi}{2}}cos2xsin^2xdx\)
b) \(\int_{-1}^{1}\left | 2^2-2^{-x} \right |dx\)
c) \(\int_{-1}^{2} \frac{(x+1)(x+2)(x+3)}{x^2}dx\)
d) \(\int_{-1}^{\frac{\pi }{2}} (sinx+cosx)^2dx\)
e) \(\int_{-1}^{\pi } (x+sinx)^2dx\)
g) \(\int_{0}^{\pi }(x+sinx)^2dx\)
Phương pháp giải
- Sử dụng công thức hạ bậc đưa về tích phân các hàm lượng giác cơ bản.
- Xét dấu, phá dấu giá trị tuyệt đối của hàm số dưới dấu tích phân.
- Biến đổi hàm số dưới dấu tích phân về các hàm đa thức, phân thức cơ bản và tính tích phân.
- Biến đổi hàm số dưới dấu tích phân về dạng tổng, hiệu hai phân thức đơn giản đã biết cách tính tích phân.
- Thu gọn biểu thức \( (\sin x+\cos x)^2\) đưa về các hàm số lượng giác cơ bản.
- Khai triển biểu thức dưới dấu tích phân, kết hợp với công thức hạ bậc, phương pháp tích phân từng phần để tính tích phân.
Hướng dẫn giải
Câu a
Biến đổi biểu thức dưới dấu tích phân ta có:
\(cos2x.sin^2x=cos2x\frac{1-cos2x}{2}= \frac{1}{2}cos2x -\frac{1}{2}cos^22x\)
\(=\frac{1}{2}cos2x-\frac{1}{4}(1+cos4x)=\frac{1}{2}cos2x - \frac{1}{4}cos4x-\frac{1}{4}\)
Do đó
\(\int_{0}^{\frac{\pi }{2}}cos2x sin^2x dx=\int_{0}^{\frac{\pi }{2}} \left ( \frac{1}{2}cos2x -\frac{1}{4}cos4x- \frac{1}{4} \right )dx\)
\(=\frac{1}{4}sin2x \bigg|_{0}^{\frac{\pi }{2}}-\frac{1}{16}sin4x \bigg|_{0}^{\frac{\pi }{2}}- \frac{1}{4}x\bigg|_{0}^{\frac{\pi }{2}}=-\frac{\pi }{8}\)
Câu b
Ta có: \(\left\{\begin{matrix} 2^x-2^{-x}\geq 0 \ \ \forall x\in [0;1]\\ 2^x-2^{-x}\leq 0 \ \ \forall x\in [-1;0) \end{matrix}\right.\)
Do đó: \(\int_{-1}^{1}\left | 2^x-2^{-x} \right |dx= \int_{-1}^{0}(2^{-x}-2^x)dx+ \int_{0}^{1}(2^{x}-2^{-x})dx\)
\(=\left ( -\frac{2^{-x}}{ln2}-\frac{2^x}{ln2} \right ) \bigg|^0_{-1}+ \left ( \frac{2^x}{ln2}+\frac{2^{-x}}{ln2} \right )\bigg|^1_{0}\)
\(=-\frac{1}{ln2}-\frac{1}{ln2}+\frac{2}{ln2}+\frac{1}{2ln2}+ \frac{2}{ln2}+\frac{1}{2ln2}-\frac{1}{ln 2}-\frac{1}{ln2}=\frac{1}{ln2}\)
Câu c
Ta có
\(\frac{(x+1)(x+2)(x+3)}{x^2}=x+6x+\frac{6}{x^2}+\frac{11}{x}\)
Do đó: \(\int_{1}^{2}\frac{(x+1)(x+2)(x+3)}{x^2}dx= \int_{1}^{2}\left ( x+6x+\frac{6}{x^2}+\frac{11}{x} \right )dx\)
\(=\left ( \frac{x^2}{2}+6x-\frac{6}{x} +11lnx \right )\Bigg|^2_1\)
\(=2+12-3+11ln2-\frac{1}{2}+6-6=\frac{21}{2}+11ln2\)
Câu d
Phân tích biểu thức dưới dấu tích phân ta được:
\(\frac{1}{x^2-2x-3}=\frac{1}{(x+1)(x-3)}=\frac{1}{4} \left ( \frac{1}{x-3}-\frac{1}{x+1} \right )\)
Do đó:
\(\int_{0}^{2}\frac{1}{x^2-2x-3}dx=\frac{1}{4}\int_{0}^{2} \left (\frac{1}{x-3}-\frac{1}{x+1} \right )dx\)
\(=\frac{1}{4}ln\left | \frac{x-3}{x+1} \right | \Bigg |^2_0= \frac{1}{4}\left ( ln\frac{1}{3} -ln3 \right )=-\frac{1}{2}ln3\)
Câu e
Ta có
\((sinx+cosx)^2=1+sin2x\)
Do đó: \(\int_{0}^{\frac{\pi }{2}}(sinx+cosx)^2dx=\int_{0}^{\frac{\pi }{2}}(1+sin2x)dx\)
\(=\left ( x-\frac{1}{2}cos2x \right )\Bigg |_0^{\frac{\pi }{2}}= \frac{\pi }{2}+\frac{1}{2}+\frac{1}{2}=\frac{\pi }{2}+1\)
Câu g
\(\int_{0}^{\pi }(x+sinx)^2dx= \int_{0}^{\pi }(x^2+2xsinx+sin^2x)dx\)
\(=\int_{0}^{\pi }(x^2+2xsin x+\frac{1}{2}-\frac{1}{2}cos2x)dx\)
\(=\left ( \frac{x^3}{3} +\frac{1}{2}x -\frac{1}{4}sin2x \right ) \Bigg|^{\pi}_0\)
\(=\frac{\pi ^3}{3}+\frac{\pi }{2}+2\int_{0}^{\pi }x sinx dx\)
Xét \(\int_{0}^{\pi }x sinx dx.\) Áp dụng phương pháp tính tích phân từng phần bằng cách đặt:
\(\left\{\begin{matrix} u=x\\ dv=sinx dx \end{matrix}\right.\Rightarrow \left\{\begin{matrix} du=dx\\ v=-cosx \end{matrix}\right.\)
Ta được
\(\int_{0}^{\pi }x sin dx = - x cosx \bigg|^{\pi}_0+ \int_{0}^{\pi }cosx dx= \pi+sinx \bigg|^{\pi}_0=\pi\)
Vậy \(\int_{0}^{\pi } (x+sinx)^2dx=\frac{\pi ^3}{3}+\frac{\pi }{2}+2\pi= \frac{\pi ^3}{3}+\frac{5\pi }{2}\)
1.7. Giải bài 7 trang 127 SGK Giải tích 12
Xét hình phẳng D giới hạn bởi \(y=2\sqrt{1-x^2}\) và \(y=2(1-x)\)
a) Tính diện tích hình D
b) Quay hình D xung quanh trục Ox. Tính thể tích khối tròn xoay được tạo thành.
Phương pháp giải
a) Hình phẳng được giới hạn bởi đường các đồ thị hàm số \(y=f(x);\) \(y=g(x)\) và các đường thẳng \(x=a; \, \, x=b \, (a
b) Thể tích khối tròn xoay có được khi quay hình phẳng D giới hạn bởi các đường \(x=a,x=b,y=f(x),y=g(x)\) quanh \(Ox\) là \(V = \pi \int\limits_a^b {\left| {{f^2}\left( x \right) - {g^2}\left( x \right)} \right|dx} \)
Hướng dẫn giải
Câu a
Phương trình hoành độ giao điểm của hai đồ thị là:
\(\eqalign{
& 2\sqrt {1 - {x^2}} = 2(1 - x) \Leftrightarrow \left\{ \matrix{
1 - x \ge 0 \hfill \cr
1 - {x^2} = {(1 - x)^2} \hfill \cr} \right. \cr
& \Leftrightarrow \left\{ \matrix{
x \le 1 \hfill \cr
2{x^2} - 2x = 0 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
x \le 1 \hfill \cr
\left[ \matrix{
x = 0 \hfill \cr
x = 1 \hfill \cr} \right. \hfill \cr} \right. \Leftrightarrow \left[ \matrix{
x = 0 \hfill \cr
x = 1 \hfill \cr} \right. \cr} \)
Đồ thị của hàm số \(y = 2\sqrt {1 - {x^2}} \) là một nửa elip \({x^2} + {{{y^2}} \over 4} = 1\) với \(y ≥ 0.\)
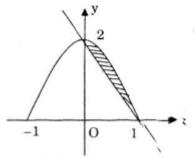
Từ đồ thị trên ta có, diện tích của D:
\(\eqalign{
& S = \int_0^1 {\left[ {2\sqrt {1 - {x^2}} - 2(1 - x)} \right]} dx \cr
& = 2\left[ {\int_0^1 {\sqrt {1 - {x^2}} dx - \int_0^1 {(1 - x)dx} } } \right] \cr} \)
Tính \(\int_0^1 {\sqrt {1 - {x^2}} } dx\):
Đặt \(x = sin t\) , ta có: \(dx = cost dt\); \(x=0 \Rightarrow t= 0\); \(x=1 \Rightarrow t={\pi \over 2}\)
Suy ra
\(\eqalign{
& \int_0^1 {\sqrt {1 - {x^2}} } dx = \int_0^{{\pi \over 2}} {\sqrt {1 - {{\sin }^2}t} } .costdt \cr
& = \int_0^{{\pi \over 2}} {{\mathop{\rm cost}\nolimits} .costdt = \int_0^{{\pi \over 2}} {{{\cos }^2}tdt} } \cr
& = {1 \over 2}\int_0^{{\pi \over 2}} {(1 + \cos 2t)dt = {1 \over 2}} \left[ {t + {1 \over 2}\sin 2t} \right]\left| {_0^{{\pi \over 2}}} \right. = {\pi \over 4} \cr
& \int_0^1 {(1 - x)dx = (x - {{{x^2}} \over 2})\left| {_0^1} \right.} = {1 \over 2} \cr
& \Rightarrow D = 2({\pi \over 4} - {1 \over 2}) = {\pi \over 2}-1 \cr} \)
Câu b
Dựa vào hình trên ta có thể tích cần tìm là:
\(\begin{array}{l}
V = \pi \int\limits_0^1 {\left[ {{{\left( {2\sqrt {1 - {x^2}} } \right)}^2} - {{\left( {2\left( {1 - x} \right)} \right)}^2}} \right]dx} \\
= \pi \int\limits_0^1 {\left[ {4\left( {1 - {x^2}} \right) - 4{{\left( {1 - x} \right)}^2}} \right]dx}
\end{array}\)
\(\eqalign{
&= 4\pi \int_0^1 {\left[ {(1 - {x^2}) - (1 - {x})^2} \right]} dx \cr
& = 8\pi \int_0^1 {(x - {x^2}} )dx = 8\pi\left( {{{{x^2}} \over 2} - {{{x^3}} \over 3}} \right)\left| {_0^1} \right. \cr
& = 8\pi ({1 \over 2} - {1 \over 3}) = {{4\pi } \over 3} \, \, (đvdt). \cr} \)
2. Bài tập trắc nghiệm
2.1. Giải bài 1 trang 127 SGK Giải tích 12
Tính \(\frac{\int dx}{\sqrt{1-x}}\) kết quả
(A) \(\frac{C}{ \sqrt{1-x}}\)
(B) \(C\sqrt{1-x}\)
(C) \(-2\sqrt{1-x}+C\)
(D) \(\frac{2}{\sqrt{1-x}}+C\)
Phương pháp giải
Sử dụng phương pháp đưa vào vi phân để làm bài toán hoặc sử dụng phương pháp đổi biến.
Chú ý nguyên hàm cơ bản: \(\int {\frac{1}{{2\sqrt u }}du} = \sqrt u + C\)
Hướng dẫn giải
Ta có
\(\displaystyle \int {{{dx} \over {\sqrt {1 - x} }}} = - \int {{{d(1 - x)} \over {\sqrt {1 - x} }}} \) \( = -2.\int {\dfrac{{d\left( {1 - x} \right)}}{{2\sqrt {1 - x} }}} \) \( = - 2\sqrt {1 - x} + C.\)
Chọn đáp án C
2.2. Giải bài 2 trang 128 SGK Giải tích 12
Tính \(\int 2^{\sqrt{x}}.\frac{ln2}{\sqrt{x}}dx\), kết quả sai là
(A) \(2^{\sqrt{x}+1}+C\)
(B) \(2(2^{\sqrt{x}}-1)+C\)
(C) \(2(2^{\sqrt{x}}+1)+C\)
(D) \(2^{\sqrt{x}}+C\)
Phương pháp giải
- Đổi biến tìm nguyên hàm đã cho.
- Hàm số \(F(x)\) là nguyên hàm của hàm số \(f(x)\) thì hàm số \(F(x) + C\) cũng là nguyên hàm của hàm số.
Hướng dẫn giải
Đặt \(t = \sqrt x \) \( \Rightarrow dt = \dfrac{1}{{2\sqrt x }}dx \Rightarrow \dfrac{{dx}}{{\sqrt x }} = 2dt\). Khi đó,
\(\int {{2^{\sqrt x }}.\dfrac{{\ln 2}}{{\sqrt x }}dx} \) \( = \int {{2^t}.\ln 2.2dt} \) \( = 2.\int {d\left( {{2^t}} \right)} \) \( = {2.2^t} + C = {2.2^{\sqrt x }} + C\).
Do đó D sai.
Chọn đáp án D
2.3. Giải bài 3 trang 128 SGK Giải tích 12
Tích phân \(\int_{0}^{\pi}cos^2x sinxdx\) bằng
(A) \(-\frac{2}{3}\)
(B) \(\frac{2}{3}\)
(C) \(\frac{3}{2}\)
(D)
Phương pháp giải
Dùng phương pháp đưa vào vi phân để tính tích phân.
Hướng dẫn giải
Ta có
\(\begin{array}{l}
\int\limits_0^\pi {{{\cos }^2}x.\sin xdx = - \int\limits_0^\pi {{{\cos }^2}xd\left( {\cos x} \right)} } \\
= \left. { - \dfrac{{{{\cos }^3}x}}{3}} \right|_0^\pi = \dfrac{1}{3} + \dfrac{1}{3} = \dfrac{2}{3}.
\end{array}\)
Chọn đáp án B
2.4. Giải bài 4 trang 128 SGK Giải tích 12
Cho hai tích phân \(\int_0^{{\pi \over 2}} {{{\sin }^2}xdx,} \int_0^{{\pi \over 2}} {{{\cos }^2}xdx} \) , hãy chỉ ra khẳng định đúng:
A. \(\int_0^{{\pi \over 2}} {{{\sin }^2}xdx} > \int_0^{{\pi \over 2}} {{{\cos }^2}xdx} \)
B. \(\int_0^{{\pi \over 2}} {{{\sin }^2}xdx} < \int_0^{{\pi \over 2}} {{{\cos }^2}xdx} \)
C. \(\int_0^{{\pi \over 2}} {{{\sin }^2}xdx} = \int_0^{{\pi \over 2}} {{{\cos }^2}xdx} \)
D. Không so sánh được
Phương pháp giải
- Sử dụng các công thức biến đổi lượng giác.
- Áp dụng phương pháp đổi biến để tính tích phân và so sánh.
Hướng dẫn giải
Nếu đặt \(\displaystyle u = {\pi \over 2} - x\) thì \(dx=-du\) và
\(\eqalign{
& \int_0^{{\pi \over 2}} {{{\sin }^2}xdx = \int_{{\pi \over 2}}^0 {{{\sin }^2}} } ({\pi \over 2} - u)( - du) \cr
& = \int_0^{{\pi \over 2}} {{{\cos }^2}} udu = \int_0^{{\pi \over 2}} {{{\cos }^2}} xdx \cr} \)
Chọn đáp án C
2.5. Giải bài 5 trang 128 SGK Giải tích 12
Diện tích hình phẳng giới hạn bởi các đường cong
Câu a: \(y=x^3\) và \(y=x^5\) bằng
(A) 0
(B) -4
(C) \(\frac{1}{6}\)
(D) 2
Câu b: \(y=x+sinx\) và \(y=x\) (\(0 \le x \le 2\pi\)) bằng:
(A) -4
(B) 4
(C) 0
(D) 1
Phương pháp giải
Hình phẳng được giới hạn bởi đường các đồ thị hàm số \(y=f(x);\) \(y=g(x)\) và các đường thẳng \(x=a; \, \, x=b \, (a
Hướng dẫn giải
Câu a
Xét phương trình: \(x^3=x^5\Leftrightarrow x=-1;x=0;x=1\)
Do đó diện tích cần tìm là:
\(S= \int_{-1}^{0}(x^5-x^3)dx+\int_{0}^{1}(x^3-x^5)dx\)
\(=\left ( \frac{x^6}{6}-\frac{x^4}{4} \right ) \bigg|^0_{-1}+ \left ( \frac{x^4}{4} -\frac{x^6}{6}\right )\bigg|^1_{0} =\frac{1}{12}+\frac{1}{12}=\frac{1}{6}.\)
Chọn đáp án C
Câu b
Xét phương trình: \(x+sinx = x\Leftrightarrow sinx = 0\Leftrightarrow x=0;x\pi; x=2\pi\)
Do đó: \(S = \int_0^\pi s inxdx - \int_0^{2\pi } s inxdx = - cosx{|_{{\pi _0}}} + cosx{|_{2\pi }}_0 = 2 + 2 = 4\)
Chọn đáp án B
2.6. Giải bài 6 trang 128 SGK Giải tích 12
Cho hình phẳng giới hạn bởi các đường \(y=\sqrt{x}\) và \(y=x\) quay xung quanh trục Ox. Thể tích của khối tròn xoay tạo thành bằng:
(A) 0
(B) \(-\pi\)
(C) \(\pi\)
(D) \(\frac{\pi}{6}\)
Phương pháp giải
Quay hình phẳng được giới hạn bởi các đồ thị hàm số \(y=f(x); \, \, y=g(x)\) và các đường thẳng \(x=a;\, \, y=b \, (a
Hướng dẫn giải
Phương trình hoành độ giao điểm của hai đường thẳng \(y = \sqrt x\) và \(y = x\) là:
\(x = \sqrt x ⇔ x = 0\) hoặc \(x = 1\)
Thể tích của khối tròn xoay tạo thành bằng:
\(V = \pi \int\limits_0^1 {\left| {{{\left( {\sqrt x } \right)}^2} - {x^2}} \right|dx} \) \(= \pi \int\limits_0^1 {\left| {x - {x^2}} \right|dx} \)
Với \(0 \le x \le 1\) thì \(x \ge {x^2}\) nên:
\(\displaystyle V = \pi \int_0^1 {(x - {x^2}} )dx = \pi \left[ {{{{x^2}} \over 2} - {{{x^3}} \over 3}} \right]\left| {_0^1} \right. = {\pi \over 6}\)
Chọn đáp án D
Tham khảo thêm
- doc Giải bài tập SGK Toán 12 Bài 1: Nguyên hàm
- doc Giải bài tập SGK Toán 12 Bài 2: Tích phân
- doc Giải bài tập SGK Toán 12 Bài 3: Ứng dụng của tích phân trong hình học



