Giải bài tập SGK Toán 12 Ôn tập chương 4: Số phức

Thế nào là phần thực, phần ảo, mô đun của một số phức? Viết công thức tính mô đun của số phức theo phần thực phần ảo của nó?

Hướng dẫn giải

Khái niệm phần thực, phần ảo của số phức:

Số phức \(z = a + bi\) có phần thực là \(a\), phần ảo là \(b\) (\(a,b\in\mathbb{R}\) và \(i^2=-1\)).

Công thức tính môđun của số phức:

Số phức \(z = a + bi\) được biểu diễn bới điểm \(M(a,b)\) trên mặt phẳng toạ độ.

Độ dài của vectơ  là môđun của số phức \(z\), kí hiệu là \(\left| z \right| = \overrightarrow {OM} = \sqrt {{a^2} + {b^2}} .\)

Tìm mối liên hệ giữa khái niêm môđun và khái niệm giá trị tuyệt đối của số thực.

Hướng dẫn giải

Mỗi số thực a được gọi là số phức có phần ảo bằng 0.

Ta có: \(a\in\mathbb{R} \Rightarrow a=a+0i.\)

Mô đun của số thực a là

\(|a+0i|=\sqrt{(a^2+0^2 )}=|a|\)

Như vậy với một số thực, môđun chính là giá trị tuyệt đối của nó.

Nêu định nghĩa số phức liên hợp với số phức z. Số phức nào bằng số phức liên hợp của nó?

Hướng dẫn giải

Số phức liên hợp của số phức \(z = a + bi\) là \(a-bi\) kí hiệu là \(\overline z = a - bi.\)

Ta có: \(z = \overline z \Leftrightarrow \left\{ \begin{array}{l} a = a\\ b = - b \end{array} \right. \Leftrightarrow b = 0.\)

Vậy số phức z bằng số phức liên hợp của nó \(\bar{z}\) khi và chỉ khi z là số thực.

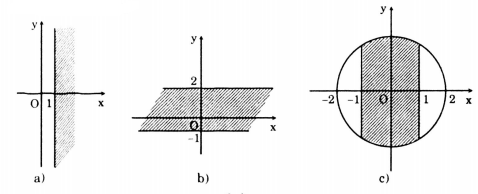
ố phức thỏa mãn điều kiện nào thì có điểm biểu diễn ở phần gạch chéo trong các hình a, b , c?

Phương pháp giải

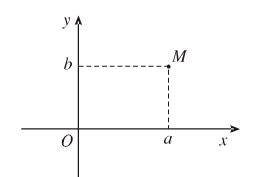
Số phức \(z = a + bi\) được biểu diễn bới điểm \(M(a,b)\) trên mặt phẳng toạ độ.

Hướng dẫn giải

Câu a

\(z=x+yi\) với \(x\geq 1\) là các số phức có phần thực lớn hơn hoặc bằng 1.

Câu b

\(z=x+yi\) với \(-1\leq x\leq 2\) là các số phức có phần ảo thuộc đoạn [-1;2].

Câu c

\(z=x+yi\) với \(x^2+y^2\leq 4\) và \(-1\leq x\leq 1\) là các số phức có phần thực thuộc đoạn [-1;1] và môđun không vượt quá 2.

Trên mặt phẳng tọa độ, tìm tập hợp biểu diễn của các số phức z thỏa mãn điều kiện:

a) Phần thực của z bằng 1

b) Phần ảo của z bằng -2

c) Phần thực của z thuộc đoạn [-1; 2], phần ảo của z thuộc đoạn [0; 1]

d) \(|z|\leq 2\)

Phương pháp giải

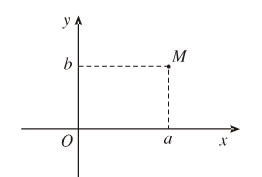
Số phức \(z = a + bi\) được biểu diễn bới điểm \(M(a,b)\) trên mặt phẳng toạ độ.

Hướng dẫn giải

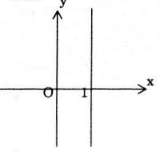
Câu a

Những điểm trên mặt phẳng phức biểu diễn cho các số phức z có phần thực bằng 1 là những điểm thuộc đường thẳng x=1.

Câu b

Những điểm trên mặt phẳng phức biểu diễn cho các số phức z có phần ảo bằng -2 là những điểm thuộc đường thẳng y=-2.

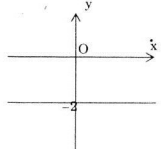
Câu c

Những điểm trên mặt phẳng phức biểu diễn cho các số phức z có phần thực thuộc đoạn [-1;2], phần ảo thuộc đoạn [0;1] là miền mặt phẳng được gạch sọc như hình vẽ bên.

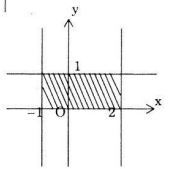
Câu d

Những điểm trên mặt phẳng phức biểu diễn cho các số phức z thỏa mãn \(\left| z \right| \le 2\) là một hình tròn tâm O(0;0) có bán kính R=2 (kể cả biên) như hình vẽ.

 Tìm các số thực x, y sao cho

a) \(3x+yi=2y+1+(2-x)i\)

b) \(2x+y-1=(x+2y-5)i\)

Phương pháp giải

Áp dụng định nghĩa hai số phức bằng nhau:

Số phức bằng nhau \(a + bi = c + di \Leftrightarrow\) \(a=c\) và \(b=d.\)​

Hướng dẫn giải

Câu a

Ta có

\(3x+yi=2y+1(2-x)i\)

\(\Leftrightarrow \left\{\begin{matrix} 3x=2y+1\\ y=2-x \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x=1\\ y=1 \end{matrix}\right.\)

Câu b

Ta có

\(2x+y-1=(x+2y-5)i\)

\(\Leftrightarrow (2x+y-1)+(0i)=0+(x+2y-5)i \\ \Leftrightarrow \left\{\begin{matrix} 2x+y-1=0\\ x+2y-5=0 \end{matrix}\right.\Leftrightarrow x=-1,y=3\)

Chứng tỏ rằng với mọi số thực z, ta luôn phần thực và phần ảo của nó không vượt quá mô đun của nó.

Phương pháp giải

Gọi \(z = a + bi \Rightarrow \left| z \right| = \sqrt {{a^2} + {b^2}} \), so sánh \(a\) với \( \left| z \right|\) và \(b\) với \( \left| z \right|\)

Hướng dẫn giải

Giả sử \(z = a + bi\)

Khi đó: \(\left| z \right| = \sqrt {{a^2} + {b^2}}\)

Từ đó suy ra

\(\begin{array}{l}
\sqrt {{a^2} + {b^2}} \ge \sqrt {{a^2}} = \left| a \right| \ge a \Rightarrow \left| z \right| \ge a\\
\sqrt {{a^2} + {b^2}} \ge \sqrt {{b^2}} = \left| b \right| \ge b \Rightarrow \left| z \right| \ge b
\end{array}\)

Thực hiện các phép tính sau

a) \((3+2i)\left [ (2-i)+(3-2i) \right ]\)
b) \((4-3i)+\frac{1+i}{2+i}\).
c) \((1+i)^2-(1-i)^2\).
d) \(\frac{3+i}{2+i}-\frac{4-3i}{2-i}\).

Phương pháp giải

Thực hiện các phép tính theo đúng thứ tự nhân, chia trước, công trừ sau, trong ngoặc trước, ngoài ngoặc sau.

Hướng dẫn giải

Câu a

\((3+2i)\left [ (2-i)+(3-2i) \right ]=(3+2i)(5-3i)=15+6+(10-9)i=21+i\).

Câu b

\((4-3i)+\frac{1+i}{2+i}=(4-3i)+\frac{(1+i)(2-i)}{2^2+1^2}=4-3i+\left ( \frac{3}{5}+\frac{1}{5}i \right )= \frac{23}{5}-\frac{14}{5}i\).

Câu c
Ta có
\({(1 + i)^2} = {1^2} + 2i + {i^2} = 1 + 2i - 1 = 2i.\)

\({(1 - i)^2} = {1^2} - 2i + {i^2} = - 2i.\)

Vậy: \((1+i)^2-(1-i)^2=4i\)

Câu d

Ta có

\(\frac{3+i}{2+i}=\frac{(3+i)(2-i)}{2^2+1^2}=\frac{7}{5}-\frac{2}{5}i\)

\(\frac{4-3i}{2-i}=\frac{(4-3i)(2+i)}{2^2+1^2}=\frac{11}{5}-\frac{2}{5}i\)

Vậy: \(\frac{3+i}{2+i}-\frac{4-3i}{2-i}=-\frac{4}{5}+\frac{1}{5}i\)

Giải các phương trình sau trên tập số phức

a) (3+4i)z + (1-3i) = 2+5i

b) (4+7i)z - (5-2i) = 6iz

Phương pháp giải

Thực hiện các bước giải tương tự như với một phương trình trên tập số thực, điểm khác biệt là các phép toán thực hiện trên tập số phức.

Hướng dẫn giải

Câu a

\(\begin{array}{l} (3 + 4i)z + (1 - 3i) = 2 + 5i\\ \Leftrightarrow (3 + 4i)z = 1 + 8i \Leftrightarrow z = \frac{{1 + 8i}}{{3 + 4i}}\\ \Leftrightarrow z = \frac{{(1 + 8i)(3 - 4i)}}{{(3 + 4i)(3 - 4i)}} = \frac{7}{5} + \frac{4}{5}i. \end{array}\)

Vậy \(z=\frac{7}{5} + \frac{4}{5}i.\)

Câu b

\(\begin{array}{l} (4 + 7i)z - (5 - 2i) = 6iz\\ \Leftrightarrow (4 + i)z = 5 - 2i \Leftrightarrow z = \frac{{5 - 2i}}{{4 + i}}\\ \Leftrightarrow z = \frac{{\left( {5 - 2i} \right)(4 - i)}}{{17}} = \frac{{18}}{{17}} - \frac{{13}}{{17}}i. \end{array}\)

Vậy: \(z = \frac{{18}}{{17}} - \frac{{13}}{{17}}i.\)

Giải các phương trình sau trên tập số phức

a) \(3z^2+7z+8=0.\)

b) \(z^4-8=0.\)

c) \(z^4-1=0.\)

Phương pháp giải

Các căn bậc hai của số thực \(a<0\) là \(\pm i\sqrt a.\)​

Xét phương trình bậc hai \(ax^2 + bx + c = 0\) với \(a,b,c\in \mathbb{R},a\ne0.\)

Đặt \(\Delta=b^2-4ac\):

Nếu \(\Delta=0\) thì phương trình có một nghiệm kép (thực) \(x=-\frac{b}{2a}.\)

Nếu \(\Delta>0\) thì phương trình có hai nghiệm thực \(x_{1,2}=\frac{-b\pm \sqrt \Delta}{2a}.\)

Nếu \(\Delta<0\) thì phương trình có hai nghiệm phức \({x_{1,2}} = \frac{{ - b \pm i\sqrt {\left| \Delta \right|} }}{{2a}}.\)

Hướng dẫn giải

Câu a

Xét phương trình: \(3z^2+7z+8=0.\)

Ta có \(\Delta =7^2-96=-47\)

Vậy phương trình có hai nghiệm \({z_1} = \frac{{ - 7 - i\sqrt {47} }}{6},{z_2} = \frac{{ - 7 + i\sqrt {47} }}{6}.\)

Câu b

Xét phương trình \(z^4-8=0.\)

Đặt \(t=z^2\), phương trình trở thành: \({t^2} - 8 = 0 \Rightarrow t = \pm \sqrt 8\)

Với \(t=\sqrt 8\Rightarrow z^2=\sqrt8\) ta có: \({z_1}{,_2} = \pm \sqrt {\sqrt 8 } = \sqrt[4]{8}\) là nghiệm của phương trình.

Với \(t=-\sqrt8\Rightarrow z^2=-8\) ta có: \({z_3}{,_4} = \pm i\sqrt 8\) là nghiệm của phương trình

Câu c

Xét phương trình \(z^4-1=0.\)

Đặt \(t=z^2\), phương trình trở thành: \({t^2} - 1 = 0 \Rightarrow t = \pm 1\)

Với \(t=1\Rightarrow z^2=1\) ta có: \({z_1}{,_2} = \pm1\) là nghiệm của phương trình.

Với \(t=-1\Rightarrow z^2=-1\) ta có: \({z_3}{,_4} = \pm i\) là nghiệm của phương trình

Tìm hai số phức, biết tổng của chúng bằng 3 và tích của chúng bằng 4

Phương pháp giải

Từ dữ kiện của đề bài, ta có hai số phức cần tìm là nghiệm của một phương trình bậc hai với hệ số thực, ta lập và giải phương trình từ đó sẽ có được hai số phức cần tìm.

Hướng dẫn giải

Gọi hai số phức cần tìm là \(z_1\) và \(z_2.\)

Ta có: \(z_1+z_2=3,z_1.z_2=4\)

Hai số phức \(z_1\) và \(z_2\) là nghiệm của phương trình:

\((z - {z_1})(z - {z_2}) = 0 \Leftrightarrow {z^2} - ({z_1} + {z_2})z + {z_1}{z_2} = 0\)

Hay: \(z^2 - 3z+4 = 0.\)

Ta có: \(\Delta = - 7.\)

Vậy hai số cần tìm là: \(z=\frac{3+\sqrt{7}}{2}; z=\frac{3-\sqrt{7}}{2}\).

Cho hai số phức \(z_1, z_2\). Biết rằng \(z_1 + z_2\) và \(z_1. z_2\) là hai số thực. Chứng minh rằng \(z_1, z_2\) là hai nghiệm của một phương trình bậc hai với hệ số thực.

Phương pháp giải

Đặt \(z_1 + z_2 = a\); \(z_1. z_2 = b; a, b ∈ \mathbb R\). Khi đó \({z_1},{z_2}\) là nghiệm của phương trình \({z^2} - az + b = 0\).

Hướng dẫn giải

Đặt \(z_1 + z_2 = a\); \(z_1. z_2 = b; a, b ∈ \mathbb R\)

Khi đó, \(z_1\) và \(z_2\) là hai nghiệm của phương trình  

\(\begin{array}{l}
\,\,\,\,\left( {z - {z_1}} \right)\left( {z - {z_2}} \right) = 0\\
\Leftrightarrow {z^2} - z.{z_2} - z.{z_1} + {z_1}{z_2} = 0\\
\Leftrightarrow {z^2} - \left( {{z_1} + {z_2}} \right)z + {z_1}{z_2} = 0\\
\Leftrightarrow {z^2} - az + b = 0
\end{array}\)

Đó là phương trình bậc hai đối với hệ số thực. Suy ra điều phải chứng minh.

Số nào trong các số sau là số thực?

(A) \((\sqrt{3}+2i) - (\sqrt{3-2i})\)

(B) \((2+i\sqrt{5}) + (2-i\sqrt{5})\)

(C) \((1+i\sqrt{3})^2\)

(D) \(\frac{\sqrt{2}+i}{\sqrt{2}-i}\)

Phương pháp giải

Số phức \(z\) là số thực nếu phần ảo của nó bằng \(0\).

Hướng dẫn giải

Hai số số phức \(2 + i\sqrt 5 \) và \(2 - i\sqrt 5 \) là các số phức liên hợp, tổng của chúng là một số thực.

Chọn đáp án B

Số nào trong các số sau là số thuần ảo?

(A) \((\sqrt{2}+3i) + (\sqrt{2-3i})\)

(B) \((\sqrt{2}-3i)(\sqrt{2+3i})\)

(C) \((2+2i)^2\)

(D) \(\frac{3+2i}{2-3i}\)

Phương pháp giải

Số thuần ảo là số phức có phần thực bằng \(0\)

Hướng dẫn giải

Ta tìm phần thực của các số đã cho

(A) \(\left( {\sqrt 2  + 3i} \right) + \left( {\sqrt 2  - 3i} \right) \) \(= \sqrt 2  + 3i + \sqrt 2  - 3i = 2\sqrt 2 \) là số thực.

(B) \(\left( {\sqrt 2  + 3i} \right)\left( {\sqrt 2  - 3i} \right)\) \( = {\left( {\sqrt 2 } \right)^2} - {\left( {3i} \right)^2} = 2 + 9 = 11\) là số thực.

(C) \({\left( {2 + 2i} \right)^2} = 4 + 8i - 4 = 8i\) là số thuần ảo.

(D) \(\displaystyle\frac{{2 + 3i}}{{2 - 3i}} = \frac{{{{\left( {2 + 3i} \right)}^2}}}{{\left( {2 - 3i} \right)\left( {2 + 3i} \right)}} \) \(\displaystyle = \frac{{4 + 12i - 9}}{{4 + 9}} = \frac{{ - 5}}{{13}} + \frac{{12}}{{13}}i\) không là số thuần ảo.

Chọn đáp án (C)

Đẳng thức nào trong các đẳng thức sau là đúng?

A. \({i^{1997}}= -1\)       

B. \({i^{2345}} = {\rm{ }} i\)

C. \({i^{2005}} = 1\)           

D. \({i^{2006}} = {\rm{ }} - i\)

Phương pháp giải

Sử dụng kết quả đã chứng minh ở bài 4 - SGK trang 136

\(\begin{array}{l}
{i^{4n}} = {i^0} = 1\\
{i^{4n + 1}} = {i^1} = i\\
{i^{4n + 2}} = {i^2} = - 1\\
{i^{4n + 3}} = {i^3} = - i
\end{array}\)

Hướng dẫn giải

Ta có

\(\begin{array}{l}
\left( A \right).\,\,{i^{1977}} = {i^{1976 + 1}} = {i^{494.4 + 1}} = {i^1} = i\\
\left( B \right).\,\,{i^{2345}} = {i^{2344 + 1}} = {i^{586.4 + 1}} = {i^1} = i\\
\left( C \right).\,\,{i^{2005}} = {i^{2004 + 1}} = {i^{501.4 + 1}} = {i^1} = i\\
\left( D \right).\,\,{i^{2006}} = {i^{2004 + 2}} = {i^{501.4 + 2}} = {i^2} = - 1
\end{array}\)

Chọn đáp án (B)

Đẳng thức nào trong các đẳng thức sau là đúng?

A. \({\left( {1 + i} \right)^{8}} =- 16\)

B. \({\left( {1 + i} \right)^{8}} =16i\)

C. \({\left( {1 + i} \right)^{8}} = 16\)

D. \({\left( {1 + i} \right)^{8}} =- 16i\)

Phương pháp giải

Tính \({\left( {1 + i} \right)^2}\), sau đó tính \({\left( {1 + i} \right)^4}\), sau đó \({\left( {1 + i} \right)^8}\).

Hướng dẫn giải

\(\begin{array}{l}
{\left( {1 + i} \right)^2} = {1^2} + 2i + {i^2} = 2i\\
\Rightarrow {\left( {1 + i} \right)^4} = {\left( {{{\left( {1 + i} \right)}^2}} \right)^2} = {\left( {2i} \right)^2} = - 4\\
\Rightarrow {\left( {1 + i} \right)^8} = {\left( {{{\left( {1 + i} \right)}^4}} \right)^2} = {\left( { - 4} \right)^2}=16
\end{array}\)

Chọn đáp án C

Biết rằng nghịch đảo của số phức \(z\) bằng số phức liên hợp của nó, trong các kết luận sau, kết luận nào là đúng?

A. \(z ∈ R\)                             B. \(|z| = 1\)

C. \(z\) là một số thuần ảo       D. \(|z| = -1\)

Phương pháp giải

Sử dụng công thức \(z.\overline z  = {\left| z \right|^2}\)

Hướng dẫn giải

Ta có

\(\dfrac{1}{z} = \overline z  \Rightarrow z.\overline z  = 1 \) \(\Leftrightarrow {\left| z \right|^2} = 1 \Leftrightarrow \left| z \right| = 1\)

Chọn đáp án (B)

Trong các kết luận sau, kết luận nào là sai?

A. Môdun của số phức \(z\) là một số thực

B. Môdun của số phức \(z\) là một số phức

C. Môdun của số phức \(z\) là một số thực dương

D. Môdun của số phức \(z\) là một số thực không âm.

Phương pháp giải

\(z = a + bi \Rightarrow \left| z \right| = \sqrt {{a^2} + {b^2}} \)

Hướng dẫn giải

\(z = a + bi \Rightarrow \left| z \right| = \sqrt {{a^2} + {b^2}}  \ge 0\).

Do đó C sai vì mô đun của số phức \(z\) vẫn có thể bằng \(0\).

Cụ thể khi \(z=0\) thì \(\left| z \right| =0\).

Chọn đáp án (C)