Giải bài tập SGK Toán 12 Bài 1: Số phức

Tìm phần thực và phần ảo của số phức z, biết

a) \(\small z = 1 - \pi i.\)

b) \(\small z = \sqrt{2} - 1\)

c) \(\small z = 2\sqrt{2}\)

d) \(\small z = -7i\)

Phương pháp giải

Số phức \(z = a + bi\) có phần thực là \(a\), phần ảo là \(b\) (\(a,b\in\mathbb{R}\) và \(i^2=-1\)).

Hướng dẫn giải

Câu a: Số phức \(\small z = 1 - \pi i\)  có phần thực bằng 1, phần ảo bằng \(\pi.\)

Câu b: Số phức \(\small z = \sqrt{2} - 1\) có phần thực bằng \(\sqrt 2\), phần ảo bằng -1.

Câu c: Số phức \(\small z = 2\sqrt{2}\) có phần thực bằng \(2\sqrt 2\), phần ảo bằng 0.

Câu d: Số phức \(\small z = -7i\) có phần thực bằng 0, phần ảo bằng -7.

Tìm các số thực x và y, bết

a) \(\small (3x - 2) + (2y + 1)i = (x + 1) - (y - 5)i.\)

b) \(\small (1 - 2x) - i\sqrt{3} = \sqrt{5} + (1 - 3y)i.\)

c) \(\small (2x + y) + (2y - x)i = (x - 2y + 3) + (y + 2x + 1)i.\)

Phương pháp giải

Áp dụng định nghĩa hai số phức bằng nhau:

Số phức bằng nhau \(a + bi = c + di \Leftrightarrow\) \(a=c\) và \(b=d.\)​

Hướng dẫn giải

Câu a

 \(\small (3x - 2) + (2y + 1)i = (x + 1) - (y - 5)i \Leftrightarrow \left\{\begin{matrix} 3x-2=x+1\\ 2y+1=-(y-5) \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x=\frac{3}{2}\\ y=\frac{4}{3} \end{matrix}\right.\) 

Câu b

 \(\small (1 - 2x) - i\sqrt{3} = \sqrt{5} + (1 - 3y)i\Leftrightarrow \left\{\begin{matrix} 1-2x=\sqrt{5}\\ 1-3y=-\sqrt{3} \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x=\frac{1-\sqrt{5}}{2}\\ y=\frac{1+\sqrt{3}}{3} \end{matrix}\right.\)  

Câu c

 \(\small (2x + y) + (2y - x)i = (x - 2y + 3) + (y + 2x + 1)i\Leftrightarrow \left\{\begin{matrix} 2x+y=x-2y+3\\ 2y-x=y+2x+1 \end{matrix}\right.\)

 ⇔ \(\left\{\begin{matrix} x+3y =3\\ -3x+y=1 \end{matrix}\right.\) ⇔ \(\left\{\begin{matrix} x=0\\ y=1 \end{matrix}\right.\).

Trên mặt phẳng toạ độ, tìm tập hợp điểm biểu diễn các số phức z thoả mãn điều kiện:

a) Phần thực của z bằng -2

b) Phần ảo của z bằng 3

c) Phần thực của z thuộc khoảng (-1; 2)

d) Phần ảo của z thuộc đoạn [1; 3]

e) Phần thực và phần ảo của z đều thuộc đoạn [-2; 2]

Phương pháp giải

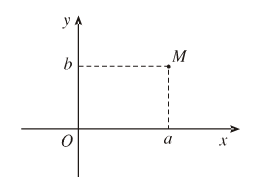
Số phức \(z = a + bi\) được biểu diễn bới điểm \(M(a,b)\) trên mặt phẳng toạ độ.

Hướng dẫn giải

Câu a

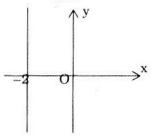
Tập hợp các điểm biểu diễn số phức z có phần thực bằng -2 là đường thẳng song song với trục Oy, cắt trục Ox tại điểm có tọa độ (-2;0) như hình vẽ:

Câu b

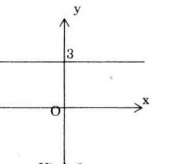
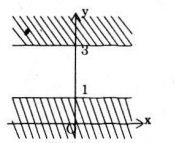
Tập hợp các điểm biểu diễn số phức z có phần ảo bằng 3 là một đường thẳng song song với trục Ox và cắt trục Oy tại điểm có tọa độ (0;3) như hình vẽ:

Câu c

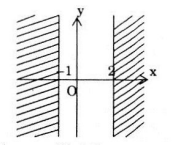
Tập hợp các điểm trên mặt phẳng phức biểu diễn cho số phức z có phần thực thuộc khoảng (-1;2) là một phần mặt phẳng được giới hạn bởi hai đường thẳng x=-1 và x=2 như hình vẽ, không kể các điểm nằm trên hai đường thẳng x=-1 và x=2:

Câu d

Tập hợp các điểm trên mặt phẳng phức biểu diễn cho số phức z có phần ảo thuộc đoạn [1;3] là phần mặt phẳng phức giới hạn bởi các đường y=1 và y=3, như hình vẽ, lấy cả những điểm trên đường thẳng y=1 và y=3:

Câu e

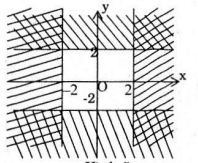
Tập hợp các điểm biểu diễn số phức z có phần thực và phần ảo đều thuoovj đoạn [-2;2] là phần mặt phẳng giới hạn bởi các đường x=-2; x=2; y-2; y=2 như hình vẽ, lấy tất cả nhứng điểm trên biên:

Tính |z| với

a) \(\small z=-2+i\sqrt{3}\)

b) \(\small z=\sqrt{2}-3i\)

c) \(\small z = -5\)

d) \(\small z=i\sqrt{3}\)

Phương pháp giải

Số phức \(z = a + bi\)  (\(a,b\in\mathbb{R}\)).  Môđun của số phức \(z\), kí hiệu \(\left | z \right |\) được xác định bởi công thức \(\left| z \right| = \sqrt {{a^2} + {b^2}} .\)

Hướng dẫn giải

Câu a

\(|z| = \sqrt {{{\left( { - 2} \right)}^2} + {{\left( {\sqrt 3 } \right)}^2}}  = \sqrt 7 \)    

Câu b

 \(\left | z \right |= \sqrt{(\sqrt{2})^{2}+(-3)^{2}}=\sqrt {11}\) .

Câu c

 \(\left | z \right |=\sqrt{(-5)^{2}}=5\).                                         

Câu d

\(\left | z \right |=\sqrt{(\sqrt{3})^{2}}=\sqrt 3\). 

Trên mặt phẳng toạ độ, tìm tập hợp điểm biểu diễn các số phức z thoả mãn điều kiện:

a) |z| = 1

b) |z| ≤ 1

c) 1 < |z| ≤ 2

d) |z| = 1 và phần ảo của z bằng 1

Phương pháp giải

Đặt \(z=x+yi (x,y\in\mathbb{R})\) khi đó trên mặt phẳng toạ độ Oxy, điểm M(x;y) biểu diễn số phức z.

Dựa vào dữ kiện đề bài ta xác định tập hợp các điểm biểu diễn số phức z.

Hướng dẫn giải

Câu a

Đặt \(z=x+yi (x,y\in\mathbb{R})\)

Ta có |z| = 1 ⇔  = 1 ⇔ x2 + y2 = 1

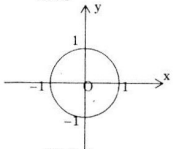
Vậy tập hợp điểm biểu diễn số phức z là đường tròn tam O, bán kính bằng 1.

Câu b

Ta có |z| ≤ 1 ⇔  ≤ 1 ⇔ x2 + y2 ≤ 1.

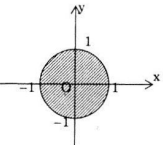
Vậy tập hợp điểm biểu diễn số phức z là hình tròn tâm O, bán kính bằng 1 (kể cả các điểm trên đường tròn x2+y2=1).

Câu c

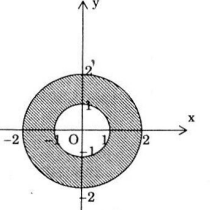
Ta có 1<|z| ≤ 2 ⇔ 1 <  ≤ 2 ⇔ 1 < x2 + y2 ≤ 4.

Vậy tập hợp điểm biểu diễn số phức z là phần nằm giữa đường tròn tâm O, bán kính bằng 1 (không kể điểm trên đường tròn này) và đường tròn tâm O, bán kính bằng 2 (kể cả các điểm trên đường tròn này).

Câu d

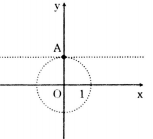
Ta có |z| = 1 ⇔  = 1 ⇔ x2 + y2 = 1 và phần ảo của z bằng 1 tức y = 1.

Suy ra x = 0 và y = 1.

Vậy tập hợp các điểm cần tìm là điểm A(0;1).

Tìm , biết

a) \(\small z = 1 - i\sqrt{2}\)

b) \(\small z = -\sqrt{2} + i\sqrt{3}\)

c) \(\small z = 5\)

d) \(\small z = 7i\)

Phương pháp giải

Số phức liên hợp của số phức \(z = a + bi\) là \(a-bi\) kí hiệu là \(\overline z = a - bi.\)

Hướng dẫn giải

Câu a: \(\bar z = 1 + i\sqrt{2}\)

Câu b: \(\bar z = -\sqrt{2} - i\sqrt{3}\)

Câu c:  = 5

Câu d:  = -7i