Giải bài tập SGK Toán 12 Bài 3: Ứng dụng của tích phân trong hình học

Tính diện tích hình phẳng giới hạn bởi các đường

a) \(y = x^2, y = x + 2\)

b) \(y = |lnx|, y = 1\)

c) \(y = (x - 6)^2, y = 6x- x^2\)

Phương pháp giải

Cho hai hàm số  \(y = f\left( x \right);\;\;y = g\left( x \right)\) liên tục trên đoạn  \(\left[ {a;\;b} \right]\). Gọi \(D\) là hình phẳng được giới hạn bởi đồ thị hai hàm số trên và các đường thẳng  \(x = a;\;\;x = b\). Khi đó diện tích của hình phẳng \(D\) được tính bởi công thức: \({S_D} = \int\limits_a^b {\left| {f\left( x \right) - g\left( x \right)} \right|dx} \)

Hướng dẫn giải

Câu a

Xét phương trình

\(x^2=x+2\Leftrightarrow x^2-x-2=0\Leftrightarrow x=-1;x=2\)

⇒ Diện tích hình phẳng giới hạn bởi đường cong \(y=x^2\) và đường thẳng \(y=x+2\) là:

\(S=\int_{1}^{2} \left | x^2-(x+2) \right |dx= \int_{1}^{2}\left | x^2-x-2 \right |dx\)

Vì \(x^2-x-2\leq 0\) khi \(-1\leq x\leq 2\)

nên \(S=-\int_{1}^{2}(x^2-x-2)dx= \left ( -\frac{x^3}{3} +\frac{x^2}{2} +2x \right ) \Bigg|^2_1\)

\(=\left ( -\frac{8}{3}+2+4 \right )-\left ( \frac{1}{3}+\frac{1}{2}-2 \right )= \frac{9}{2}\)

Vậy \(S=\frac{9}{2}\) (đvdt)

Câu b

Xét phương trình: \(\left | lnx \right | =1\Leftrightarrow x=e;x=\frac{1}{e}\)

Do đó diện tích cần tìm là: \(S=\int_{1}^{e} \left |\left | lnx \right |-1 \right |dx\)

Ta có: \(\left | lnx \right | = \left\{\begin{matrix} ln x \ neu \ x\geq 1\\ -lnx \ neu \ 0< x\leq 1 \end{matrix}\right.\)

Do đó

\(\begin{array}{l}S = \int\limits_{\frac{1}{e}}^1 {\left| { - {\mathop{\rm lnx}\nolimits}  - 1} \right|dx}  + \int\limits_1^e {\left| {\ln x - 1} \right|dx} \\ = \int\limits_{\frac{1}{e}}^1 {\left| {{\mathop{\rm lnx}\nolimits}  + 1} \right|dx}  + \int\limits_1^e {\left| {\ln x - 1} \right|dx} \end{array}\)

Ta có: \(\left\{ \begin{array}{l}\forall x \in \left[ {\frac{1}{e};1} \right] \Rightarrow  - 1 \le \ln x \le 0 \Rightarrow 0 \le \ln x + 1 \le 1\\\forall x \in \left[ {1;e} \right] \Rightarrow 0 \le \ln x \le 1 \Rightarrow  - 1 \le \ln x - 1 \le 0\end{array} \right.\)

Vậy: \(S = \int\limits_{\frac{1}{e}}^1 {\left( {{\mathop{\rm lnx}\nolimits}  + 1} \right)dx}  - \int\limits_1^e {\left( {\ln x - 1} \right)dx} \)

\( = \int\limits_{\frac{1}{e}}^1 {dx}  + \int\limits_{\frac{1}{e}}^1 {\ln xdx}  + \int\limits_1^e {xdx}  - \int\limits_1^e {\ln xdx} \)

\(\begin{array}{l} =  - \frac{1}{e} + e + \int\limits_{\frac{1}{e}}^1 {\ln xdx}  - \int\limits_1^e {\ln xdx} \\ =  - \frac{1}{e} + e + \left. {x\ln x} \right|_{\frac{1}{e}}^1 - \int\limits_{\frac{1}{e}}^1 {dx}  - \left. {x\ln x} \right|_1^e + \int\limits_1^e {dx} \\ =  - \frac{1}{e} + e + \frac{2}{e} - 1 - 1 = \frac{1}{e} + e - 2\end{array}\)

Câu c

Xét phương trình: \((x-6)^2=6x-x^2\Leftrightarrow 2x^2-18x+36=0\)

\(\Leftrightarrow x=3;x=6\)

Do đó diện tích cần tìm là:

\(S=\int_{3}^{6} \left | (x-6)^2-(6x-x^2) \right |dx= \int_{3}^{6} \left | 2x^2-18x+36 \right |dx\)

\(=-2\int_{3}^{6}(x^2-9x+18)dx\)

(Vì: \(2x^2-18x+36 \leq 0\) khi \(3\leq x\leq 6\))

\(=-2\left ( \frac{x^3}{3}-\frac{9}{2}x^2+18x \right ) \bigg|^6_3=-2\left ( 8-\frac{45}{2} \right )=9\) (đvdt).

Tính diện tích hình phẳng giới hạn bởi đường cong \(y = {x^2} + 1\), tiếp tuyến với đường này tại điểm \(M(2;5)\) và trục \(Oy\).

Phương pháp giải

• Viết phương trình tiếp tuyến của đồ thị hàm số \(y=f(x)\) tại điểm \(M(x_0;y_0)\) theo công thức: \(y=y'(x_0) (x-x_0)+y_0.\)
• Tìm nghiệm \(x_1; x_2\) của phương trình hoành độ giao điểm của đồ thị hàm số bài cho và tiếp tuyến vừa tìm được.
• Dựa vào công thức tính diện tích hình phẳng được giới hạn bởi các đồ thị hàm số để tính diện tích hình phẳng cần tìm.

Hướng dẫn giải

Ta có: \(y'=2x.\)

Phương trình tiếp tuyến của đồ thị hàm số \(y=x^2+1\) tại \(M(2;\, \, 5)\) là: \(y = y'\left( 2 \right)\left( {x - 2} \right) + 5 = 4\left( {x - 2} \right) + 5 = 4x - 3.\)

Phương trình tiếp tuyến là \(y = 4x - 3\).

Phương trình hoành độ giao điểm của đồ thị hàm số với tiếp tuyến là: \({x^2} + 1 =4x - 3 \Leftrightarrow {x^2} - 4x + 4= 0 \\ ⇔ (x-2)^2=0 ⇔ x = 2.\)

Do đó diện tích phải tìm là

\(S=\int_{0}^{2}|x^{2}+1 -4x+3|dx \) \(=\int_{0}^{2}(x^{2}-4x+4)dx\)

\(=\left. {\left( {\dfrac{{{x^3}}}{3} - \dfrac{{4{x^2}}}{2} + 4x} \right)} \right|_0^2 \)

\(=\dfrac{8}{3} \, \, (đvdt)\).

Parabol \(y = {{{x^2}} \over 2}\) chia hình tròn có tâm tại gốc tọa độ, bán kính \(2\sqrt2\) thành hai phần. Tìm tỉ số diện tích của chúng.

Phương pháp giải

• Xác định các phần của đường tròn được chia bởi parabol (P).
• Sử dụng công thức tính diện tích hình phẳng để tính diện tích hai phần được chia sau đó tính tỉ số của hai phần diện tích.

Hướng dẫn giải

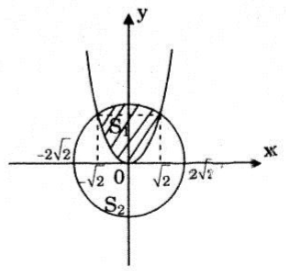
Từ hình vẽ ta có

\(S_1=2 \int_{0}^{2} \left [ \sqrt{8-x^2}-\frac{x^2}{2} \right ] dx\)

\(=2 \int_{0}^{2} \sqrt{8-x^2}- \int_{0}^{2} x^2 dx\)

\(=2 \int_{0}^{2} \sqrt{8-x^2}dx-\frac{x^3}{3}\Bigg |^2_0\)

\(=2 \int_{0}^{2} \sqrt{8-x^2}dx-\frac{8}{3}\)

Đặt \(x=2\sqrt{2}sint\Rightarrow dx=2\sqrt{2}costdt\)

Khi x = 0 thì  t = 0; khi x = 2 thì \(t=\frac{\pi }{4}\)

\(\Rightarrow 2\int_{0}^{2}\sqrt{8-x^2}dx=4\sqrt{2} \int_{0}^{\frac{\pi }{4}}\sqrt{8-8sin^2t}.cost dt\)

\(=16 \int_{0}^{\frac{\pi }{4}}cos^2t dt=8 \int_{0}^{\frac{\pi }{4}}(1+cos2t)dt=2\pi+4\)

\(\Rightarrow S_1=2\pi+4-\frac{8}{3}=\frac{6\pi+4}{3}\)

Gọi S là diện tích hình tròn tâm O bán kính \(R=2\sqrt{2}\) ta có \(S=8\pi .\)

Từ đó \(\Rightarrow S_2=S-S_1=8\pi-\frac{6\pi+4}{3}= \frac{18 \pi-4}{3}\)

Vậy \(\frac{S_2}{S_1}=\frac{18\pi -4}{6\pi+4}=\frac{9\pi-2}{3\pi+2}\)

Tính thể tích khối tròn xoay do hình phẳng giới hạn bởi các đường sau quay quanh trục Ox:

a) \(\small y = 1 - x^2 , y = 0\)

b) \(\small y = cosx, y = 0, x = 0, x = \pi\)

c)  \(\small y = tanx, y = 0, x = 0,x=\frac{\pi }{4}\)

Phương pháp giải

Cho hình phẳng được giới hạn bởi hai đồ thị hàm số  \(y = f\left( x \right);y = g\left( x \right) \, \) và hai đường thẳng \(x=a; \, \, x=b \, \, \, (a

Hướng dẫn giải

Câu a

Xét phương trình: \(1-x^2=0\Leftrightarrow x=1;x=-1\)

Áp dụng công thức (5) ta có thể tích cần tìm là:

\(V= \pi \int_{-1}^{1}(1-x^2)^2dx= \pi \int_{-1}^{1} (1-2x^2+x^4)dx\)

\(=\left ( x-\frac{2}{3}x^3+\frac{x^5}{5} \right ) \Bigg|^1_{-1}= \pi\left [ \left ( 1-\frac{2}{3} +\frac{1}{5}\right ) - \left ( -1+\frac{2}{3}-\frac{1}{5} \right )\right ]\)

\(=\pi \left ( 2-\frac{4}{3}+\frac{2}{5} \right )=\frac{16 \pi}{15}\)

Câu b

Áp dụng công thức (5) ta có:

\(V=\pi \int_{0}^{\pi }cos^2x dx=\pi \int_{0}^{\pi }\frac{1+cos2x}{2}dx\)

\(=\frac{\pi }{2} \int_{0}^{\pi }dx+\frac{\pi }{4} \int_{0}^{\pi }cos2x d2x\)

\(=\frac{\pi }{2}x \Bigg|^{\pi}_0+ \frac{\pi }{4}sin 2x \Bigg|^{\pi}_0= \frac{\pi ^2}{2}\)

Câu c

Áp dụng công thức (5) ta có:

\(V=\pi \int_{0}^{\frac{\pi }{4}}tan^2x dx= \pi \int_{0}^{\frac{\pi }{4}} \left ( \frac{1}{cos^2x}-1 \right )dx\)

\(=\pi \int_{0}^{\frac{\pi }{4}}\frac{dx}{cos^2x}-\pi \int_{0}^{\frac{\pi }{4}}dx\)

\(=\pi tan x \Bigg |_{0}^{\frac{\pi }{4}}- \pi x\Bigg |_{0}^{\frac{\pi }{4}}= \pi -\frac{\pi ^2}{4}=\pi \left ( 1-\frac{\pi }{4} \right )\)

Cho tam giác vuông OPM có cạnh OP nằm trên trục Ox. Đặt  \(\widehat{POA}=\alpha\) và \(OM=R, \left ( 0\leq \alpha \leq \frac{\pi }{3}, R>0 \right )\)

Gọi V là khối tròn xoay thu được khi quay tam giác đó xung quanh Ox (H.63).

a) Tính thể tích của V theo α và R     

b) Tìm \(\small \alpha\) sao cho thể tích V là lớn nhất.  

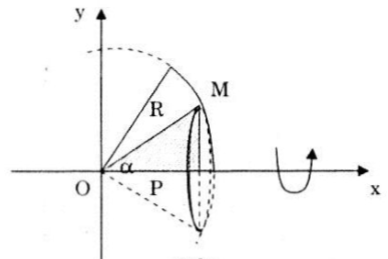
Phương pháp giải

a) Hình phẳng cần tính thể tích được giới hạn bởi đoạn thẳng \(OM, \, \, MP\) và trục hoành.

Xác định phương trình đường thẳng \(OM\) và sử dụng công thức tính thể tích để tính thể tích khối tròn xoay   cần tính.

b) Tính được thể tích của khối tròn xoay   theo \(\alpha.\) Khảo sát hàm số \(V=V(\alpha)\) để tìm thể tích lớn nhất.

Hướng dẫn giải

Câu a

Ta có: \(OP=R.cos\alpha ; PM=R.sin\alpha\)

⇒ Diện tích đáy B của khối tròn xoay V là: \(B= \pi .PM^2=\pi .R^2.sin^2\alpha .\)

Theo công thức (4) ta có thể tích của khối tròn xoay V là: 

\(V=\frac{1}{3}B.OP=\frac{1}{3}.R.cos\alpha .\pi .R^2.sin^2\alpha\)

\(=\frac{1}{3}\pi .R^3.cos\alpha .sin^2\alpha =\frac{1}{3}\pi .R^3(cos\alpha -cos^3\alpha )\)

Với \(=\left ( 0\leq \alpha \leq \frac{\pi }{3} \right )\)

Câu b

Ta có V lớn nhất \(\Leftrightarrow cos\alpha -cos^3\alpha\) lớn nhất.

Xét hàm số \(f(t)=t-t^3(t=cos\alpha )\). Khi \(\alpha \in \left ( 0;\frac{\pi }{3} \right )\) thì \(t \in \left ( \frac{1}{2};1\right )\)

Ta có: \(f'(t) = 1 - 3{t^2} = 0 \Leftrightarrow \left[ \begin{array}{l}
t = \frac{1}{{\sqrt 3 }}\\
t = \frac{1}{2}
\end{array} \right.\)

Ta có bảng biến thiên

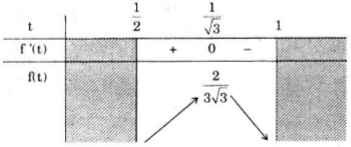
⇒ f(t) lớn nhất bằng \(\frac{2}{3\sqrt{3}}\) khi \(t=\frac{1}{\sqrt{3}}\)

Hay \(cos \alpha -cos^3\alpha\) lớn nhất: \(\frac{2}{3\sqrt{3}}\) đạt được khi \(cos\alpha =\frac{1}{\sqrt{3}}\)

Vậy \(V_{max}=\frac{2\pi \sqrt{3}}{27}R^3\) khi \(cos\alpha =\frac{1}{\sqrt{3}}\)