Giải bài tập SGK Toán 12 Bài 4: Hàm số mũ. Hàm số lôgarit
Phần hướng dẫn giải bài tập Hàm số mũ Hàm số lôgarit sẽ giúp các em nắm được phương pháp và rèn luyện kĩ năng các giải bài tập từ SGK Giải tích 12 Cơ bản và Nâng cao.
Mục lục nội dung

1. Giải bài 1 trang 77 SGK Giải tích 12
Vẽ đồ thị của các hàm số
a) \(\small y = 4^x\)
b) \(y=\left ( \frac{1}{4} \right )^{x}\)
Phương pháp giải
Thực hiện các bước khảo sát đơn giản như sau
Xét hàm số \(y=a^x(a>0,a\ne1)\)
- Nếu a>1 thì hàm số đồng biến trên R, nếu 0
- Lập bảng giá trị tung độ, hoành đồ các điểm mà đồ thị hàm số đi qua.
- Vẽ đồ thị.
Hướng dẫn giải
Câu a
Xét hàm số \(\small y = 4^x\)
Tập xác định D=R.
Do a=4>0 nên hàm số đồng biến trên R.
Bảng giá trị
|
x |
-1 |
0 |
1 |
|
y |
\(\frac{1}{4}\) |
1 |
4 |
Đồ thị hàm số
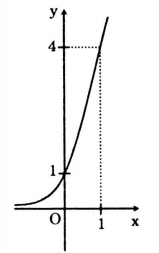
Câu b
Xét hàm số \(\small y = \left ( \frac{1}{4} \right )^x\)
Tập xác định D=R.
Do \(\small a=\frac{1}{4}<1\) nên hàm số nghịch biến trên R.
Bảng giá trị
|
x |
-1 |
0 |
1 |
|
y |
4 |
1 |
\(\small \frac{1}{4}\) |
Đồ thị hàm số
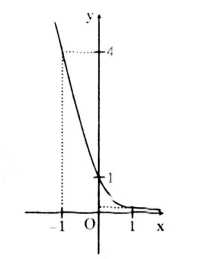
2. Giải bài 2 trang 77 SGK Giải tích 12
Tính đạo hàm của các hàm số
a) \(\small y = 2xe^x + 3sin2x\)
b) \(\small y = 5x^2 - 2xcosx\)
c) \(y=\frac{x+1}{3^{x}}\)
Phương pháp giải
Ta sử dụng các công thức tính đạo hàm của hàm số mũ:
- Hàm số \(y=e^x\) có đạo hàm với mọi \(x\) và: \(\left ( e^x \right )'=e^x\)
- Hàm số \(y=a^x(a>0,a\ne 1)\) có đạo hàm tại mọi \(x\) và: \(\left( {{a^x}} \right)' = {a^x}{\mathop{\rm lna}\nolimits}\)
- Đối với hàm hợp
- \(({e^u})' = u'.{e^u}\)
- \(({a^u})' = {a^u}.\ln a.u'\)
Hướng dẫn giải
Câu a
\(\small y = 2xe^x + 3sin2x.\)
\(\begin{array}{l} y' = 2\left[ {x'{e^x} + x.({e^x})'} \right] + 3(2x)'.\cos 2x\\ = 2{e^x} + 2x{e^x} + 6\cos 2x. \end{array}\)
Câu b
\(\small y = 5x^2 - 2xcosx.\)
\(y' = 10x - ({2^x})'\cos x - {2^x}(\cos x)' = 10x - {2^x}\ln 2.\cos x + {2^x}\sin x.\)
Câu c
\(y=\frac{x+1}{3^{x}}\)
\(\begin{array}{l} y' = \frac{{\left( {x + 1} \right)'{{.3}^x} - (x + 1)({3^x})'}}{{{{({3^x})}^2}}} = \frac{{{3^x} - (x + 1){{.3}^x}\ln 3}}{{{{({3^x})}^2}}}\\ = \frac{{1 - (x + 1)\ln 3}}{{{3^x}}}. \end{array}\)
3. Giải bài 3 trang 77 SGK Giải tích 12
Tìm tập xác định của các hàm số
a) \(y= log_2(5-2x)\)
b) \(y= log_3(x^2-2x)\)
c) \(y=log_{\frac{1}{5}}\left ( x^{2} -4x+3 \right )\)
d) \(\small y=log_{0,4}\frac{3x+1}{1-x}\)
Phương pháp giải
Cho số thực dương \(a\) khác 1
Hàm số \(y=\log_ax\) được gọi là hàm số lôgarit cơ số a có tập xác định: \(D=\left( {0; + \infty } \right).\)
Hướng dẫn giải
Câu a
Hàm số \(y= log_2(5-2x)\) xác định khi \(5 - 2x > 0 \Leftrightarrow x < \frac{5}{2}.\)
Vậy tập xác định của hàm số là: \(D = \left( { - \infty ;\frac{5}{2}} \right).\)
Câu b
Hàm số \(y= log_3(x^2-2x)\) xác định khi \({x^2} - 2x > 0 \Leftrightarrow \left[ \begin{array}{l} x < 0\\ x > 2 \end{array} \right.\)
Vậy tập xác định của hàm số là: \(D = \left( { - \infty ;0} \right) \cup \left( {2; + \infty } \right).\)
Câu c
Hàm số \(y=log_{\frac{1}{5}}\left ( x^{2} -4x+3 \right )\) xác định khi \({x^2} - 4x + 3 > 0 \Leftrightarrow \left[ \begin{array}{l} x < 1\\ x > 3 \end{array} \right.\)
Vậy tập xác định của hàm số là: \(D = ( - \infty ;1) \cup \left( {3; + \infty } \right).\)
Câu d
Hàm số \(\small y=log_{0,4}\frac{3x+1}{1-x}\) xác định khi: \(\frac{{3x + 2}}{{1 - x}} > 0 \Leftrightarrow - \frac{2}{3} < x < 1\)
Vậy tập xác định của hàm số là: \(D = \left( { - \frac{2}{3};1} \right).\)
4. Giải bài 4 trang 78 SGK Giải tích 12
Vẽ đồ thị của các hàm số
a) \(y = logx\)
b) \(y=log_{\frac{1}{2}}x\)
Phương pháp giải
Xét hàm số \(y = {\log _a}x(a > 0,a \ne 1)\)
- Tập xác định: \(D = \left( {0; + \infty } \right)\)
- Nếu a>1 thì hàm số đồng biến trên \(\left( {0; + \infty } \right)\), nếu 0.
- Lập bảng giá trị tung độ, hoành đồ các điểm mà đồ thị hàm số đi qua.
- Vẽ đồ thị.
Hướng dẫn giải
Câu a
Xét hàm số \(y = logx\)
Tập xác định: \(D = \left( {0; + \infty } \right)\).
a=10>1 nên hàm số đồng biến trên \(\left( {0; + \infty } \right)\).
Bảng giá trị
|
x |
\(\frac{1}{10}\) |
1 |
10 |
|
y |
-1 |
0 |
1 |
Đồ thị hàm số

Câu b
Xét hàm số \(y=log_{\frac{1}{2}}x\)
Tập xác định: \(D = \left( {0; + \infty } \right)\).
\(a=\frac{1}{2}<1\) nên hàm số nghịch biến trên \(\left( {0; + \infty } \right)\).
Bảng giá trị
|
x |
\(\frac{1}{2}\) |
1 |
2 |
|
y1 |
1 |
0 |
-1 |
Đồ thị hàm số
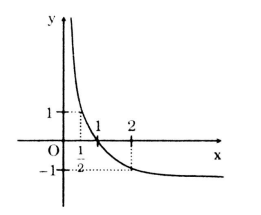
5. Giải bài 5 trang 78 SGK Giải tích 12
Tính đạo hàm của các hàm số
a) \(\small y= 3x^2 - lnx + 4sinx\)
b) \(\small y= log(x^2+ x + 1)\)
c) \(y=\frac{log_{3}x}{x}\)
Phương pháp giải
Sử dụng các công thức tính đạo hàm của hàm số lôgarit
- \(\left( {{{\log }_a}x} \right)' = \frac{1}{{x\ln a}}\)
- \(\left( {{{\log }_a}\left| x \right|} \right)' = \frac{1}{{x\ln a}}\)
- \(\left( {\ln x} \right)' = \frac{1}{x}\)
- Đối với hàm hợp
- \(\left( {{{\log }_a}u} \right)' = \frac{{u'}}{{u.\ln a}}\)
- \(\left( {\ln u} \right)' = \frac{{u'}}{{\ln u}}\)
Hướng dẫn giải
Câu a
\(y= 3x^2 - lnx + 4sinx\)
\(y' = 6x - \frac{1}{x} + 4\cos x\)
Câu b
\(\small y= log(x^2+ x + 1)\)
\(y' = \frac{{\left( {{x^2} + x + 1} \right)'}}{{({x^2} + x + 1)ln10}} = \frac{{2x + 1}}{{({x^2} + x + 1)\ln 10}}.\)
Câu c
\(y=\frac{log_{3}x}{x}\)
\(\begin{array}{l} y' = \frac{{\left( {{{\log }_3}x} \right)'x + x'.lo{g_3}x}}{{{x^2}}} = \frac{{\frac{1}{{x\ln 3}}.x + {{\log }_3}x}}{{{x^2}}}\\ = \frac{{\frac{1}{{\ln 3}} + {{\log }_3}x}}{{{x^2}}} = \frac{{\ln 3.{{\log }_3}x + 1}}{{{x^2}.\ln 3}}. \end{array}\)
Tham khảo thêm
- doc Giải bài tập SGK Toán 12 Bài 1: Luỹ thừa
- doc Giải bài tập SGK Toán 12 Bài 2: Hàm số lũy thừa
- doc Giải bài tập SGK Toán 12 Bài 3: Lôgarit
- doc Giải bài tập SGK Toán 12 Bài 5: Phương trình mũ và phương trình lôgarit
- doc Giải bài tập SGK Toán 12 Bài 6: Bất phương trình mũ và bất phương trình lôgarit
- doc Giải bài tập SGK Toán 12 Ôn tập chương 2: Hàm số lũy thừa, Hàm số mũ và Hàm số Lôgarit



