Giải bài tập SGK Toán 12 Bài 2: Hàm số lũy thừa

Tìm tập xác định của các hàm số

a) \(\small y=\left ( 1-x \right )^{\frac{-1}{3}}\)

b) \(y=\left ( 2-x^{2} \right )^{\frac{3}{5}}\)

c) \(y=\left ( x^{2}-1 \right )^{-2}\)

d) \(y=\left ( x^{2}-x-2\right )^{\sqrt{2}}\)

Phương pháp giải

Vận dụng các điều kiện xác định của hàm số lũy thừa như sau:

• Hàm số \(y=x^n\) với n nguyên dương, xác định với mọi \(x \in \mathbb{R}\).
• Hàm số \(y=x^n\), với n nguyên âm hoặc n = 0, xác định với mọi \(x \in \mathbb{R}\backslash \left\{ 0 \right\}\).
• Hàm số \(y=x^{\alpha}\), với \(\alpha\) không nguyên, có tập xác định là tập hợp các số thực dương \(\left( {0; + \infty } \right)\)

Hướng dẫn giải

Câu a

Do \(-\frac{1}{3}\) là số không nguyên nên: 

Hàm số \(\small y=\left ( 1-x \right )^{\frac{-1}{3}}\) xác định khi 1-x > 0 ⇔ x< 1.

Vậy tập xác định của hàm số là (-∞; 1).

Câu b

Do \(\frac{3}{5}\) là số không nguyên nên: 

Hàm số \(y=\left ( 2-x^{2} \right )^{\frac{3}{5}}\) xác định khi 2-x2  > 0 ⇔ \(-\sqrt2

Vậy tập xác định của hàm số là \(\left ( -\sqrt2; \sqrt2 \right )\).

Câu c

Do -2 là số nguyên âm nên:

Hàm số \(y=\left ( x^{2}-1 \right )^{-2}\) xác định khi \(x^2-1\ne0\Leftrightarrow x\ne \pm1.\)

Vậy tập xác định của hàm số là \(\mathbb{R}\backslash \left\{ { - 1;1} \right\}.\)

Câu d

Do \(\sqrt2\) là số không nguyên nên:

Hàm số \(y=\left ( x^{2}-x-2\right )^{\sqrt{2}}\) xác định khi x2-x-2 > 0 ⇔ x <-1 hoặc x > 2.

Vậy tập xác định của hàm số là (-∞;-1) ∪ (2; +∞).

Tìm các đạo hàm của các hàm số

a) \(\small y=\left ( 2x^{2} -x+1\right )^{\frac{1}{3}}\)

b) \(y=\left ( 4-x-x^{2}\right )^{\frac{1}{4}}\)

c) \(y=\left ( 3x+1\right )^{\frac{\pi }{2}}\)

d) \(y=\left ( 5-x\right )^{\sqrt{3}}\)

Phương pháp giải

Áp dụng công thức tính đạo hàm của hàm số lũy thừa

Hàm số luỹ thừa \(y = {x^\alpha }(\alpha \in \mathbb{R})\) có đạo hàm tại mọi điểm \(x>0\) và \(\left( {{x^\alpha }} \right)' = \alpha {x^{\alpha - 1}}\).

Nếu hàm số \(u=u(x)\) nhận giá trị dương và có đạo hàm trên \(J\) thì hàm số \(y = {u^\alpha }(x).\) cũng có đạo hàm trên \(J\) và \(\left( {{u^\alpha }\left( x \right)} \right)' = \alpha .{u^{\alpha - 1}}(x).u'(x)\).

Hướng dẫn giải

Câu a

\(\begin{array}{l}
y' = \frac{1}{3}\left( {2{x^2} - x + 1} \right)'{\left( {2{x^2} - x + 1} \right)^{\frac{1}{3} - 1}}\\
 = \frac{{\left( {4x - 1} \right){{\left( {2{x^2} - x + 1} \right)}^{\frac{{ - 2}}{3}}}}}{3}
\end{array}\)

Câu b

\(\begin{array}{l}
y' = \frac{1}{4}\left( {4 - x - {x^2}} \right)'{\left( {4 - x - {x^2}} \right)^{\frac{1}{4} - 1}}\\
 = \frac{1}{4}\left( { - 2x - 1} \right){\left( {4 - x - {x^2}} \right)^{\frac{{ - 3}}{4}}}
\end{array}\)

Câu c

\(\begin{array}{l}
y' = \frac{\pi }{2}\left( {3x + 1} \right)'{\left( {3x + 1} \right)^{\frac{\pi }{2} - 1}}\\
 = \frac{{3\pi }}{2}{\left( {3x + 1} \right)^{\frac{\pi }{2} - 1}}
\end{array}\)

Câu d

\(\begin{array}{l}
y' = \sqrt 3 \left( {5 - x} \right)'{\left( {5 - x} \right)^{\sqrt 3  - 1}}\\
 =  - \sqrt 3 {\left( {5 - x} \right)^{\sqrt 3  - 1}}
\end{array}\)

Khảo sát sự biến thiên và vẽ đồ thị của các hàm số

a) \(y=x^\frac{4}{3}\)

b) \(\small y=x^{-3}\)

Phương pháp giải

Các bước khảo sát sự biến thiên và vẽ đồ thị hàm số:

Bước 1: Tìm tập xác định của hàm số.

Bước 2: Tính y', tìm các điểm mà tại đó có y' bằng 0 hoặc không xác định, xét dấu y' và suy ra các chiều biến thiên của hàm số. Tìm các cực trị, các giới hạn tại vô cực và các đường tiệm cận để lập BBT của đồ thị hàm số.

Bước 3: Dựa vào bảng biến thiên và các yếu tố xác định ở trên để vẽ đồ thị hàm số.

Hướng dẫn giải

Câu a

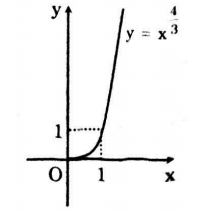
Xét hàm số \(y=x^\frac{4}{3}\)

Tập xác định: D=(0;+∞).

Sự biến thiên:\(y' = \frac{4}{3}{x^{\frac{1}{3}}} > 0,\forall x > 0\) nên hàm số luôn luôn đồng biến trên (0;+∞).

Giới hạn đặc biệt: \(\mathop {\lim }\limits_{x \to {0^ + }} y = 0;\mathop {\lim }\limits_{x \to + \infty } y = + \infty\) nên đồ thị hàm số không có tiệm cận.

Bảng biến thiên

Đồ thị của hàm số

Đồ thị hàm số đi qua điểm (1;1) và \(\left ( 2;2^\frac{4}{3} \right )\).

Câu b

Xét hàm số \(\small y=x^{-3}\)

Tập xác định: \(D = \mathbb{R}\backslash {\rm{\{ 0\} }}{\rm{.}}\)

Sự biến thiên: \(y' = - 3{x^{ - 4}} = - \frac{3}{{{x^4}}} < 0,\forall x \ne 0.\)

Giới hạn đặc biệt: \(\mathop {\lim }\limits_{x \to {0^ + }} y = + \infty ;\mathop {\lim }\limits_{x \to {0^ - }} y = - \infty ;\mathop {\lim }\limits_{x \to \pm \infty } y = 0\) nên đồ thị hàm số nhận đường thẳng y=0 làm tiệm cận ngang và nhận đường thẳng x=0 là tiệm cận đứng. 

Vậy hàm nghịch biến trong hai khoảng (-∞;0) và (0; +∞).

Bảng biến thiên

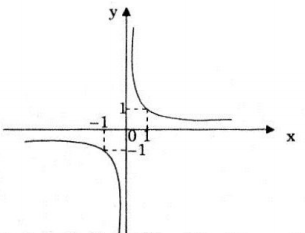
Đồ thị hàm số

Đồ thị hàm số nhận điểm (0;0) làm tâm đối xứng.

Đồ thị hàm số đi qua các điểm (1;1) và (-1;-1).

Đồ thị hàm số

Hãy so sánh các số sau với 1

a) \(\left ( 4,1 \right )^{2,7}\)

b) \(\left ( 0,2 \right )^{0,3}\)

c) \(\left ( 0,7 \right )^{3,2}\)

d) \(\left ( \sqrt{3} \right )^{0,4}\)

Phương pháp giải

Sử dụng phương pháp so sánh hai lũy thừa cùng cơ số:

\({a^{f\left( x \right)}} < {a^{g\left( x \right)}} \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}a > 1\\f\left( x \right) < g\left( x \right)\end{array} \right.\\\left\{ \begin{array}{l}0 < a < 1\\f\left( x \right) > g\left( x \right)\end{array} \right.\end{array} \right.\)

Hướng dẫn giải

Câu a

Ta có: \(1 = {\left( {4,1} \right)^0}\)

Vì \(\left\{ \matrix{  4,1 > 1 \hfill \cr   2,7 > 0 \hfill \cr}  \right. \Rightarrow {\left( {4,1} \right)^{2,7}} > {\left( {4,1} \right)^0} = 1\)

Câu b

Ta có: \(1 = {\left( {0,2} \right)^0}\)

Vì \(\left\{ \matrix{  0,2 < 1 \hfill \cr   0,3 > 0 \hfill \cr}  \right. \Rightarrow {\left( {0,2} \right)^{0,3}} < {\left( {0,2} \right)^0} = 1\)

Câu c

Ta có: \(1 = {\left( {0,7} \right)^0}\)

Vì \(\left\{ \matrix{  0,7 < 1 \hfill \cr   3,2 > 0 \hfill \cr}  \right. \Rightarrow {\left( {0,7} \right)^{3,2}} < {\left( {0,7} \right)^0} = 1\)

Câu d

Ta có: \(1 = {\left( {\sqrt 3 } \right)^0}\)

Vì \(\left\{ \matrix{  \sqrt 3  > 1 \hfill \cr   0,4 > 0 \hfill \cr}  \right. \Rightarrow {\left( {\sqrt 3 } \right)^{0,4}} > {\left( {\sqrt 3 } \right)^0} = 1\)

Hãy so sánh các cặp số sau

a) \(\left ( 3,1 \right )^{7,2}\) và \(\left ( 4,3 \right )^{7,2}\)

b) \(\left ( \frac{10}{11} \right )^{2,3}\) và \(\left ( \frac{12}{11} \right )^{2,3}\)

c) \(\left ( 0,3 \right )^{0,3}\) và \(\left ( 0,2 \right )^{0,3}\)

Phương pháp giải

Đây là bài toán so sánh hai lũy thừa có cùng số mũ.

Cho a, b và \(\alpha\) là các số thực dương ta có: \(a > b \Leftrightarrow {a^\alpha } > {b^\alpha }.\)

Hướng dẫn giải

Câu a

Vì 7,2 > 0 và 3,1 < 4,3 suy ra \(\left ( 3,1 \right )^{7,2} < \left ( 4,3 \right )^{7,2}\).

Câu b

Vì 2,3 > 0 và \(\frac{10}{11}\) < \(\frac{12}{11}\) suy ra  \(\left ( \frac{10}{11} \right )^{2,3}\) < \(\left ( \frac{12}{11} \right )^{2,3}\).

Câu c

Vì 0,3 > 0 và 0,3 > 0,2 suy ra \(\left ( 0,3 \right )^{0,3}\) > \(\left ( 0,2 \right )^{0,3}\).