Giải bài tập SGK Toán 12 Bài 1: Sự đồng biến, nghịch biến của hàm số
Hướng dẫn Giải bài tập Toán 12 Chương 1 Bài 1 sự đồng biến, nghịch biến của hàm số dưới đây sẽ giúp các em học sinh nắm vững phương pháp giải bài tập và ôn luyện tốt kiến thức. Mời các em cùng theo dõi.
Mục lục nội dung

1. Giải bài 1 trang 9 SGK Giải tích 12
Xét sự đồng biến, nghịch biến của các hàm số
a) \(y = 4 + 3x - x^2\)
b) \(y =\frac{1}{3} x^3 + 3x^2 - 7x - 2\)
c) \(y = x^4 - 2x^2 + 3\)
d) \(y = -x^3 + x^2 - 5\)
Phương pháp giải
Với bài toán xét sự đồng biến và nghịch biến của hàm số ta thực hiện bốn bước sau
- Bước 1: Tìm tập xác định của hàm số
- Bước 2: Tính đạo hàm \(f'(x)=0\). Tìm các điểm \(x_i\) (i= 1 , 2 ,..., n) mà tại đó đạo hàm bằng 0 hoặc không xác định
- Bước 3: Sắp xếp các điểm xi theo thứ tự tăng dần và lập bảng biến thiên
- Bước 4: Nêu kết luận về các khoảng đồng biến, nghịch biến của hàm số
Bên cạnh đó các em cần ôn lại các định lý về dấu của nhị thức bậc nhất và tam thức bậc hai đã học ở lớp 10 để xét dấu đạo hàm của các hàm số một cách chính xác nhất
Hướng dẫn giải
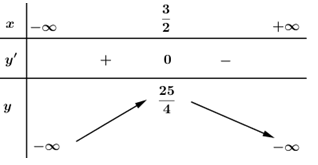
Câu a: Xét sự đồng biến, nghịch biến của hàm số \(y = 4 + 3x - x^2\)
Tập xác định: \(D=R\)
Có \(y'=3-2x\Rightarrow y'=0\) \(\Leftrightarrow 3-2x=0\) \(\Leftrightarrow x=\frac{3}{2}.\)
Bảng biến thiên
Vậy hàm số đồng biến trên khoảng \(\left( -\infty ;\frac{3}{2} \right)\) và nghịch biến trên khoảng \(\left( \frac{3}{2};+\infty \right).\)
Câu b: Xét sự đồng biến, nghịch biến của hàm số \(y ={1 \over 3}x^3\) + \(3x^2-7x - 2\)
Tập xác định: \(D=R.\)
Có \(y'={{x}^{2}}+6x-7\) \(\Rightarrow y'=0\Leftrightarrow {{x}^{2}}+6x-7=0\) \(\Leftrightarrow \left[ \begin{align} & x=1 \\ & x=-7 \\ \end{align} \right..\)
Bảng biến thiên
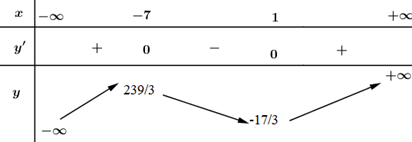
Vậy hàm số đồng biến trên các khoảng \(\left( -\infty ;-7 \right)\) và \(\left( 1;+\infty \right)\).
Hàm số nghịch biến trên \(\left( -7;\ 1 \right).\)
Câu c: Xét sự đồng biến, nghịch biến của hàm số \(y = x^4\) - \(2x^2\) +\( 3\)
Tập xác định: \(D=R\)
Có \(y'=4{{x}^{3}}-4x\) \(\Rightarrow y'=0\Leftrightarrow 4{{x}^{3}}-4x=0\)
\(\begin{array}{l}
\Leftrightarrow 4x\left( {{x^2} - 1} \right) = 0\\
\Leftrightarrow \left[ \begin{array}{l}
4x = 0\\
{x^2} - 1 = 0
\end{array} \right.\\
\Leftrightarrow \left[ \begin{array}{l}
x = 0\\
x = \pm 1
\end{array} \right.
\end{array}\)
Bảng biến thiên
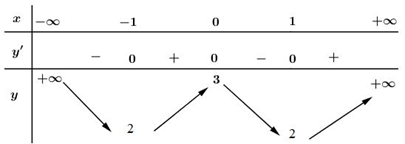
Vậy hàm số đồng biến trên các khoảng \(\left( -1;\ 0 \right)\) và \(\left( 1;+\infty \right)\)
Hàm số nghịch biến trên các khoảng \(\left( -\infty ;-1 \right)\) và \(\left( 0;\ 1 \right)\)
Câu d: Xét sự đồng biến, nghịch biến của hàm số \(y = -x^3\)+ \(x^2\) - \(5\)
Tập xác định: \(D=R\)
Có \(y'=-3{{x}^{2}}+2x\) \(\Rightarrow y'=0\Leftrightarrow -3{{x}^{2}}+2x=0\) \(\Leftrightarrow \left[ \begin{align} & x=0 \\ & x=\frac{2}{3} \\ \end{align} \right..\)
Bảng biến thiên
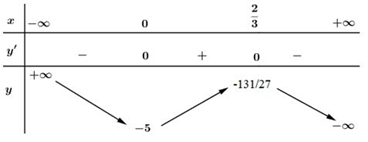
Vậy hàm số đồng biến trên khoảng \(\left( 0;\frac{2}{3} \right)\)
Hàm số nghịch biến trên các khoảng \(\left( -\infty ;0 \right)\) và \(\left( \frac{2}{3};+\infty \right)\)
2. Giải bài 2 trang 10 SGK Giải tích 12
Tìm các khoảng đơn điệu của các hàm số
a) \(y = \frac{{3x + 1}}{{1 - x}}\)
b) \(y = \frac{{{x^2} - 2x}}{{1 - x}}\)
c) \(y = \sqrt {{x^2} - x - 20} \)
d) \(y = \frac{{2x}}{{{x^2} - 9}}\)
Phương pháp giải
Với bài toán tìm khoản đơn điệu của hàm số, ta giải theo các bước sau
- Bước 1: Tìm tập xác định của hàm số
- Bước 2: Tính đạo hàm \(f'(x)=0\). Tìm các điểm \(x_i\) (i= 1 , 2 ,..., n) mà tại đó đạo hàm bằng 0 hoặc không xác định
- Bước 3: Sắp xếp các điểm xi theo thứ tự tăng dần và lập bảng biến thiên
- Bước 4: Nêu kết luận về các khoảng đồng biến, nghịch biến của hàm số
Hướng dẫn giải
Câu a: Tìm các khoảng đơn điệu của hàm số \(y=\dfrac{3x+1}{1-x}\)
Tập xác định: \(D=R\backslash \left\{ 1 \right\}.\)
Có: \(y'=\dfrac{3.1-(-1).1}{{{\left( -x+1 \right)}^{2}}}\)\(=\dfrac{4}{{{\left( -x+1 \right)}^{2}}}>0\ \forall \ x\in D.\)
Bảng biến thiên
.png)
Vậy hàm số đồng biến trên các khoảng xác định của nó là: \(\left( -\infty ;\ 1 \right)\) và \(\left( 1;+\infty \right).\)
Chú ý: Cách tính giới hạn để điền vào BBT: \(\mathop {\lim }\limits_{x \to \pm \infty } \dfrac{{3x + 1}}{{1 - x}} = - 3,\) \(\mathop {\lim }\limits_{x \to {1^ + }} \dfrac{{3x + 1}}{{1 - x}} = - \infty ,\) \(\mathop {\lim }\limits_{x \to {1^ - }} \dfrac{{3x + 1}}{{1 - x}} = + \infty \)
Câu b: Tìm các khoảng đơn điệu của hàm số \(y=\dfrac{x^{2}-2x}{1-x}\)
Tập xác định: \(D=R\backslash \left\{ 1 \right\}.\)
Có: \(y'=\dfrac{\left( 2x-2 \right)\left( 1-x \right)+{{x}^{2}}-2x}{{{\left( 1-x \right)}^{2}}}\) \(=\dfrac{-{{x}^{2}}+2x-2}{{{\left( 1-x \right)}^{2}}}\) \(=\dfrac{-\left( {{x}^{2}}-2x+2 \right)}{{{\left( 1-x \right)}^{2}}}\) \(=\dfrac{-\left( {{x}^{2}}-2x+1 \right)-1}{{{\left( 1-x \right)}^{2}}}\) \(=\dfrac{-{{\left( x-1 \right)}^{2}}-1}{{{\left( 1-x \right)}^{2}}}\) \(=-1-\dfrac{1}{{{\left( 1-x \right)}^{2}}}<0\ \forall x\in D.\)
Bảng biến thiên
.png)
Vậy hàm số nghịch biến trên các khoảng xác định của nó là: \(\left( -\infty ;\ 1 \right)\) và \(\left( 1;+\infty \right).\)
Chú ý: Cách tính giới hạn để điền vào bảng biến thiên
\(\begin{align}& \underset{x\to +\infty }{\mathop{\lim }}\,\dfrac{{{x}^{2}}-2x}{1-x}=-\infty \cr& \underset{x\to -\infty }{\mathop{\lim }}\,\dfrac{{{x}^{2}}-2x}{1-x}=+\infty \ \\ & \underset{x\to {{1}^{+}}}{\mathop{\lim }}\,\dfrac{3x+1}{1-x}=+\infty \cr&\underset{x\to {{1}^{-}}}{\mathop{\lim }}\,\dfrac{3x+1}{1-x}=-\infty \\ \end{align}\)
Câu c: Tìm các khoảng đơn điệu của hàm số \(y=\sqrt{x^{2}-x-20}\)
Có \({{x}^{2}}-x-20\ge 0\) \(\Leftrightarrow \left( x+4 \right)\left( x-5 \right)\ge 0\) \(\Leftrightarrow \left[ \begin{align} & x\le -4 \\ & x\ge 5 \\ \end{align} \right..\)
Tập xác định: \(D=\left( -\infty ;-4 \right]\cup \left[ 5;+\infty \right).\)
Có \(y'=\dfrac{2x-1}{2\sqrt{{{x}^{2}}-x-20}}\) \(\Rightarrow y'=0\Leftrightarrow 2x-1=0\)\(\Leftrightarrow x=\dfrac{1}{2}\notin D\)
Bảng biến thiên
.png)
Vậy hàm số nghịch biến trên khoảng \(\left( -\infty ;-4 \right)\) và đồng biến trên khoảng \(\left( 5;+\infty \right).\)
Chú ý: Cách tính giới hạn để điền vào BBT
\(\begin{align} & \underset{x\to -\infty }{\mathop{\lim }}\,\sqrt{{{x}^{2}}-x-20}=+\infty\cr&\underset{x\to +\infty }{\mathop{\lim }}\,\sqrt{{{x}^{2}}-x-20}=+\infty \\ & \underset{x\to {{4}^{-}}}{\mathop{\lim }}\,\sqrt{{{x}^{2}}-x-20}=0\cr& \underset{x\to {{5}^{+}}}{\mathop{\lim }}\,\sqrt{{{x}^{2}}-x-20}=0.\ \\ \end{align}\)
Câu d: Tìm các khoảng đơn điệu của hàm số \(y=\dfrac{2x}{x^{2}-9}\)
Có \({{x}^{2}}-9\ne 0\Leftrightarrow x\ne \pm 3.\)
Tập xác định: \(D=R\backslash \left\{ \pm 3 \right\}.\)
Có: \(y'=\dfrac{2\left( {{x}^{2}}-9 \right)-2x.2x}{{{\left( {{x}^{2}}-9 \right)}^{2}}}\) \(=\dfrac{-2{{x}^{2}}-18}{{{\left( {{x}^{2}}-9 \right)}^{2}}}\) \(=\dfrac{-2\left( {{x}^{2}}+9 \right)}{{{\left( {{x}^{2}}-9 \right)}^{2}}}<0\ \forall \ x\in D.\)
Bảng biến thiên
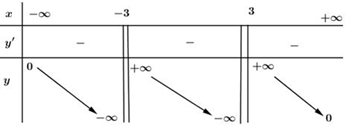
Vậy hàm số nghịch biến trên các khoảng xác định của nó là: \(\left( -\infty ;\ -3 \right);\ \left( -3;\ 3 \right)\) và \(\left( 3;\ +\infty \right).\)
Chú ý: Cách tính giới hạn để điền vào BBT
\(\begin{align}& \underset{x\to -\infty }{\mathop{\lim }}\,\dfrac{2x}{{{x}^{2}}-9}=0\cr&\underset{x\to +\infty }{\mathop{\lim }}\,\dfrac{2x}{{{x}^{2}}-9}=0 \\ & \underset{x\to -{{3}^{+}}}{\mathop{\lim }}\,\dfrac{2x}{{{x}^{2}}-9}=+\infty \cr&\underset{x\to -{{3}^{-}}}{\mathop{\lim }}\,\dfrac{2x}{{{x}^{2}}-9}=-\infty \\ & \underset{x\to {{3}^{+}}}{\mathop{\lim }}\,\dfrac{2x}{{{x}^{2}}-9}=+\infty \cr& \underset{x\to {{3}^{-}}}{\mathop{\lim }}\,\dfrac{2x}{{{x}^{2}}-9}=-\infty . \\ \end{align}\)
3. Giải bài 3 trang 10 SGK Giải tích 12
Chứng minh rằng hàm số \(y=\frac{x}{x^{2}+1}\) đồng biến trên khoảng (-1;1) và nghịch biến trên các khoảng \((-\infty; -1)\) và \((1 ; +\infty)\)
Phương pháp giải
Với bài toán khảo sát tính đơn điệu của hàm số y=f(x) ta thực hiện các bước sau: Tìm tập xác định của hàm số, tính đạo hàm f'(x), giải phương trình f'(x)=0, lập bảng biến thiên và đưa ra kết luận về sự đồng biến và nghịch biến của hàm số.
Hướng dẫn giải
Tập xác định: \(D=R.\)
Có: \(y'=\dfrac{{{x}^{2}}+1-2{{x}^{2}}}{{{\left( {{x}^{2}}+1 \right)}^{2}}}=\dfrac{1-{{x}^{2}}}{\left( {{x}^{2}}+1 \right)^2}\)
\(\Rightarrow y'=0\Leftrightarrow 1-{{x}^{2}}=0\Leftrightarrow \left[ \begin{align}& x=1 \\ & x=-1 \\ \end{align} \right..\)
Ta có: \(y' > 0 \Leftrightarrow 1 - {x^2} > 0 \) \(\Leftrightarrow - 1 < x < 1\)
Do đó hàm số đồng biến trên khoảng \(\left( -1;\ 1 \right).\)
\(y' < 0 \Leftrightarrow 1 - {x^2} < 0\) \( \Leftrightarrow \left[ \begin{array}{l}x > 1\\x < - 1\end{array} \right.\)
Do đó hàm số nghịch biến trên khoảng \(\left( -\infty ;\ -1 \right)\) và \(\left( 1;+\infty \right).\)
4. Giải bài 4 trang 10 SGK Giải tích 12
Chứng minh rằng hàm số \(y=\sqrt{2x-x^{2}}\) đồng biến trên khoảng \((0 ; 1)\) và nghịch biến trên các khoảng \((1 ; 2)\)
Phương pháp giải
Bài 4 một bài toán khảo sát tính đơn điệu của hàm số chứa căn thức, để giải bài ta cũng thực hiên qua 4 bước:
- Bước 1: Tìm tập xác định của hàm số.
- Bước 2: Tính đạo hàm \(f'(x)=0\). Tìm các điểm \(x_i\) (i= 1 , 2 ,..., n) mà tại đó đạo hàm bằng 0 hoặc không xác định.
- Bước 3: Sắp xếp các điểm xi theo thứ tự tăng dần và lập bảng biến thiên.
- Bước 4: Nêu kết luận về các khoảng đồng biến, nghịch biến của hàm số.
Sau khi khảo sát xong tính đơn điệu của hàm số ta sẽ có được điều phải chứng minh theo yêu cầu của bài 4.
Hướng dẫn giải
Xét hàm số \(y=\sqrt{2x-x^{2}}\)
Tập xác định: \(D = \left [ 0 ; 2 \right ];\)
\(y' = \frac{{2 - 2x}}{{2\sqrt {2x - {x^2}} }} = \frac{{1 - x}}{{\sqrt {2x - {x^2}} }}\)
\(y' = 0 \Leftrightarrow x = 1.\)
Bảng biến thiên
.png)
Từ bảng biến thiên ta thấy: Hàm số đồng biến trên khoảng (0;1) và nghịch biến trên khoảng (1;2).
Vậy ta có điều phải chứng minh.
5. Giải bài 5 trang 10 SGK Giải tích 12
Chứng minh các bất đẳng thức sau
a) \(\tan x > x (0 < x <\frac{\pi }{2} )\)
b) \(\tan x > x +\frac{x^3}{3} (0 < x < \frac{\pi }{2})\)
Phương pháp giải
Với dạng bài tập ở bài 5 chứng minh \(g(x)>h(x)\) với x thuộc một miền cho trước ta thường tiến hành như sau:
- Bước 1: \(g(x)>h(x)\Leftrightarrow g(x)-h(x)>0.\)
- Bước 2: Đặt \(f(x)=h(x)-g(x)\), khảo sát tính đơn điệu của hàm số \(f(x)\).
- Bước 3: Tìm x để \(f(x)=0\) (thường là hai đầu mút của miền đang xét).
- Bước 4: Từ tính đơn điệu của hàm số \(f(x)\) đưa ra kết luận cho bài toán.
Hướng dẫn giải
Câu a: Chứng minh \(\tan x > x (0 < x <\frac{\pi }{2} )\)
Để chứng minh \(tanx >x\) với mọi \(0 < x < \frac{\pi }{2}\) ta chứng minh tanx - x > 0 với mọi \(0 < x < \frac{\pi }{2}\)
Trước tiên ta cần kiểm tra xem có tồn tại giá trị nào của x đề tanx-x=0 hay không, mà trước hết ta cần thử với hai giá trị là x=0 và \(x=\frac{\pi}{2}.\)
Dễ thấy: \(tan(0)-0=0.\)
Khi đó ta tiến hành mở rộng khoảng đang xét thành nửa khoảng, cụ thể lời giải chi tiết như sau:
Xét hàm số f(x)= tanx–x liên tục trên nửa khoảng \(\left [0;\frac{\pi}{2} \right )\)
\(f'(x) = \frac{1}{{{{\cos }^2}x}} - 1 > 0\) với mọi \(x\in\left ( 0;\frac{\pi}{2} \right )\).
\(f'(x)=0\Leftrightarrow x=0.\)
Bảng biến thiên
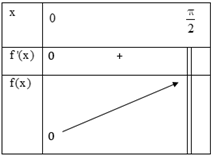
Vậy hàm số đồng biến trên \(\left [0;\frac{\pi}{2} \right )\).
Vậy với \(0 < x < \frac{\pi }{2}\) ta có \(f\left( x \right) > f\left( 0 \right) = 0 \Rightarrow tanx > x\)
Câu b: Chứng minh \(\tan x > x +\frac{x^3}{3} (0 < x < \frac{\pi }{2})\)
Tương tự câu a
Xét hàm số \(g(x) = \tan x - x - \frac{{{x^3}}}{3}\) liên tục trên \(\left[ {0;\frac{\pi }{2}} \right)\) có đạo hàm:
\(g'(x) = \frac{1}{{{{\cos }^2}x}} - 1 - {x^2} = {\tan ^2}x - {x^2}\)
\(= (tanx - x)(tanx + x) > 0,\,\forall x \in \left( {0;\frac{\pi }{2}} \right)\) (Theo câu a)
\(g'(x)=0\Leftrightarrow x=0.\)
Bảng biến thiên
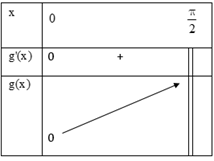
Vậy hàm số đồng biến trên \(\left[ {0;\frac{\pi }{2}} \right)\).
Vậy với \(0 < x < \frac{\pi }{2}\) ta có \(g\left( x \right) > g\left( 0 \right) \Rightarrow tanx > x + \frac{{{x^3}}}{3}\) với mọi \(x\in\left ( 0;\frac{\pi}{2} \right )\).
Nhận xét: Với dạng bài tập chứng minh f(x)>0 với x thuộc khoảng (a;b). Nếu f(a) và f(b) đề khác không, hoặc f(x) không xác định tại a và b. Thì f(x)=0 tại x0, với x0 là nghiệm của phương trình f'(x)=0, ta không cần mở rộng khoảng đang xét.
Tham khảo thêm
- docx Giải bài tập SGK Toán 12 Bài 2: Cực trị của hàm số
- docx Giải bài tập SGK Toán 12 Bài 3: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số
- docx Giải bài tập SGK Toán 12 Bài 4: Đường tiệm cận
- docx Giải bài tập SGK Toán 12 Bài 5: Khảo sát sự biến thiên và vẽ đồ thị của hàm số
- docx Giải bài tập SGK Toán 12 Ôn tập Chương 1: Ứng dụng đạo hàm để khảo sát và vẽ ĐTHS