Giải bài tập SGK Toán 9 Bài 1: Phương trình bậc nhất hai ẩn

Trong các cặp số \((-2; 1),(0;2); (-1; 0), (1,5; 3)\) và \((4; -3)\), cặp số nào là nghiệm của phương trình:

a) \(5x + 4y = 8\)

b) \(3x + 5y = -3\)

Phương pháp giải

Cặp \((x_0;\ y_0)\) là nghiệm của phương trình \(ax+by=c\) nếu khi thay \(x=x_0,\ y=y_0\) vào phương trình ta được hai vế bằng nhau. 

Hướng dẫn giải

Câu a

Thay từng cặp số đã cho vào phương trình \(5x + 4y = 8\), ta được:

\(5(-2)+4.(1)=-6\neq 8\) suy ra điểm này không là nghiệm của phương trình

\(5.(0)+4.(2)=8\) suy ra điểm này là nghiệm của phương trình

\(5.(-1)+4.(0)=-5\neq 8\) suy ra điểm này không là nghiệm của phương trình

\(5.(1,5)+4.(3)=19,5\neq 8\) suy ra điểm này không là nghiệm của phương trình

\(5.(4)+4.(-3)=8\) suy ra điểm này là nghiệm của phương trình

Vậy có hai cặp số \((0; 2)\) và \((4; 3)\) là nghiệm của phương trình \(5x + 4y = 8\)

Câu b

Thay từng cặp số đã cho vào phương trình \(3x + 5y = -3\), ta được:

\(3.(-2)+5.(1)=-1\neq -3\) suy ra điểm này không là nghiệm của phương trình

\(3.(0)+5.(2)=10\neq -3\) suy ra điểm này không là nghiệm của phương trình

\(3.(-1)+5.(0)= -3\) suy ra điểm này là nghiệm của phương trình

\(3.(1,5)+5.(3)= 19,5\neq -3\) suy ra điểm này không là nghiệm của phương trình

\(3.(4)+5.(-3)= -3\) suy ra điểm này là nghiệm của phương trình

Vậy có hai cặp số \((-1; 0)\) và \((4; -3)\) là nghiệm của phương trình \(3x + 5y = -3\)

Với mỗi phương trình sau, tìm nghiệm tổng quát của phương trình và vẽ đường thẳng biểu diễn tập nghiệm của nó:

a) \(3x - y = 2\)                                          b) \(x + 5y = 3\)

c) \(4x - 3y = -1\)                                    d) \(x +5y = 0\)

e) \(4x + 0y = -2\)                                    f) \(0x + 2y = 5\)

Phương pháp giải

1) Tìm nghiệm tổng quát của phương trình:

+) Nếu \(a \ne 0 \) thì tìm \(x\) theo \(y\). Khi đó công thức nghiệm là:

\(\left\{ \matrix{
x = \dfrac{c - by}{a} \hfill \cr 
y \in \mathbb{R} \hfill \cr} \right.\)

+) Nếu \(b \ne 0 \) thì tìm \(y\) theo \(x\). Khi đó công thức nghiệm là:

\(\left\{ \matrix{
y = \dfrac{c - ax}{b} \hfill \cr 
x \in \mathbb{R} \hfill \cr} \right.\)

2) Cách vẽ đường thẳng có phuương trình: \(ax+by=c\).

+) Nếu \(a \ne 0,\ b \ne 0\) thì vẽ đường thẳng \(y=\dfrac{-a}{b}x+\dfrac{c}{b}\)

+) Nếu \(a \ne 0,\ b=0\) thì vẽ đường thẳng \(x=\dfrac{c}{a}\) song song hoặc trùng với trục tung.

+) Nếu \(a =0,\ b \ne 0\) thì vẽ đường thẳng \(y=\dfrac{c}{a}\) song song hoặc trùng với trục hoành.

Hướng dẫn giải

Câu a

\(3x - y = 2\)

\(\left\{\begin{matrix} x\epsilon \mathbb{R}\\ y=3x-2 \end{matrix}\right.\)

Đồ thị hàm số qua \(A(0;-2);B(1;1)\)

Câu b

\(x + 5y = 3\)

\(\left\{\begin{matrix} x\epsilon \mathbb{R}\\ y=-\frac{1}{5}x+\frac{3}{5} \end{matrix}\right.\)

Đồ thị hàm số qua \(A(3;0),B(-2;1)\)

Câu c

\(4x - 3y = -1\)

\(\left\{\begin{matrix} x\epsilon \mathbb{R}\\ y=\frac{4}{3}x+\frac{1}{3} \end{matrix}\right.\)

Hàm số đi qua \(A(-1;-1),B(2;3)\)

Câu d

\(x +5y = 0\)

\(\left\{\begin{matrix} x\epsilon \mathbb{R}\\ y=-\frac{1}{5}x \end{matrix}\right.\)

Hàm số đi qua \(A(0;0),B(-5;1)\)

Câu e

\(4x + 0y = -2\)

\(\left\{\begin{matrix} x=-\frac{1}{2}\\ y\epsilon \mathbb{R} \end{matrix}\right.\)

Hàm số luôn qua điểm có hoành độ bằng \(\frac{-1}{2}\) và tung độ tùy ý

Các điểm A, B, C, D đều có hoành độ bằng \(\frac{-1}{2}\) và có tung độ bất kì.

Tập nghiệm là đường thẳng x = , qua A(; 0) và song song với trục tung.

Câu f

\(0x + 2y = 5\)

\(\left\{\begin{matrix} x\epsilon \mathbb{R}\\ y=\frac{5}{2} \end{matrix}\right.\)

Hàm số luôn qua điểm có tung độ bằng \(\frac{5}{2}\) và hoành độ tùy ý

Các điểm A, B, C, D đều có tung độ bằng \(\frac{5}{2}\) và hoành độ tùy ý.

Cho hai phương trình \(x + 2y = 4\) và \(x - y = 1\). Vẽ hai đường thẳng biểu diễn tập nghiệm của hai phương trình đó trên cùng một hệ trục tọa độ. Xác định tọa độ giao điểm của hai đường thẳng và cho biết tọa độ của nó là nghiệm của các phương trình nào.

Phương pháp giải

1) Cho phương trình: \(ax+by=c, \ (b \ne 0)\). Biến đổi \(ax+by=c \Leftrightarrow y=-\dfrac{a}{b}x+c\).

+) Cho \(x=0 \Rightarrow y=c\). Đường thẳng đi qua điểm \(A(0; c)\)

+) Cho \(y=0 \Rightarrow x=\dfrac{b.c}{a} \). Đường thẳng đi qua điểm \(B{\left( \dfrac{b.c}{a}; 0 \right)} \)

Tập nghiệm của phương trình được biểu diễn bởi đường thẳng đi qua hai điểm \(A,\ B\).

2) Hoành độ giao điểm của hai đường thẳng \(y=ax+b\) và \(y=a'x+b'\) là nghiệm của phương trình: \(ax+b=a'x+b'\). Giải phương trình tìm được \(x\) thay vào một trong hai phương trình trên tìm được tung độ giao điểm.

Hướng dẫn giải

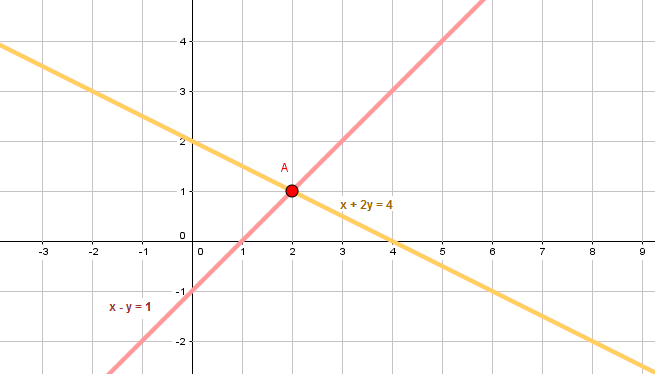
Bằng hình vẽ, ta tìm được giao điểm của điểm A là \(A(2;1)\)

Bây giờ ta sẽ tìm bằng phương pháp tính toán:

Phương trình hoành độ giao điểm (phương trình không chứa tung độ y) là:

\(\frac{4-x}{2}=x-1\Leftrightarrow 4-x=2x-2\Leftrightarrow x=2\Rightarrow y=1\)

Vậy: \(A(2;1)\)