Giải bài tập SGK Toán 8 Bài 2: Nhân đa thức với đa thức
Phần hướng dẫn giải bài tập Nhân đa thức với đa thức sẽ giúp các em nắm được phương pháp và rèn luyện kĩ năng, giải bài tập từ SGK Đại số 8 Tập 1
Mục lục nội dung
1. Giải bài 7 trang 8 SGK Toán 8 tập 1
2. Giải bài 8 trang 8 SGK Toán 8 tập 1
3. Giải bài 9 trang 8 SGK Toán 8 tập 1
4. Giải bài 10 trang 8 SGK Toán 8 tập 1
5. Giải bài 11 trang 8 SGK Toán 8 tập 1
6. Giải bài 12 trang 8 SGK Toán 8 tập 1
7. Giải bài 13 trang 9 SGK Toán 8 tập 1

1. Giải bài 7 trang 8 SGK Toán 8 tập 1
Làm tính nhân
a) \((x^2 - 2x + 1)(x - 1)\)
b) \((x^3 - 2x^2 + x - 1)(5- x)\)
Từ câu b), hãy suy ra kết quả của phép nhân: \((x^3 - 2x^2 + x - 1)( x - 5) \)
Phương pháp giải
Áp dụng
- Qui tắc nhân đa thức với đa thức.
- Qui tắc phá dấu ngoặc.
Hướng dẫn giải
Câu a
\(({x^2}-2x + 1)\left( {x-1} \right)\)
\( = {x^2}.\left( {x - 1} \right) + \left( { - 2x} \right).\left( {x - 1} \right) \)\(\,+ 1.\left( {x - 1} \right)\)
\( = {x^2}.x + {x^2}.\left( { - 1} \right) + \left( { - 2x} \right).x \)\(+ \left( { - 2x} \right).\left( { - 1} \right) + 1.x + 1.\left( { - 1} \right)\)
\(= {x^3} - {x^{2}} - 2{x^2} + 2x + x-1\)
\( = {x^3} + \left( { - {x^2} - 2{x^2}} \right) + \left( {2x + x} \right) - 1\)
\(= {x^3} - 3{x^2} + 3x-1.\)
Câu b
\(({x^3}-2{x^{2}} + x - 1)\left( {5-x} \right)\)
\( = {x^3}\left( {5 - x} \right) - 2{x^2}\left( {5 - x} \right) + x\left( {5 - x} \right)\)\(\, - 1.\left( {5 - x} \right)\)
\(= {x^3}.5 + {x^3}.\left( { - x} \right) + ( - 2{x^2}).5 \)\(+ ( - 2{x^2}).\left( { - x} \right) + x.5 + x.\left( { - x} \right) \)\(+ \left( { - 1} \right).5 + \left( { - 1} \right).\left( { - x} \right)\)
\( = 5{x^3}-{x^4}-10{x^2} + 2{x^3} + 5x-{x^2}\)\(-5 + x\)
\( = - {x^4} + \left( {5{x^3} + 2{x^3}} \right) + \left( { - 10{x^2} - {x^2}} \right)\)\(\, + \left( {5x + x} \right) - 5\)
\( = - {x^4} + 7{x^3}-11{x^2} + 6x - 5.\)
Suy ra kết quả của phép nhân
\(\matrix{
{\left( {{x^3}-2{x^2} + x - 1} \right)\left( {x - 5} \right)} \hfill \cr
{ = \left( {{x^3}-2{x^2} + x - 1} \right)\left[ { - \left( {5 - x} \right)} \right]} \hfill \cr
{ = - \left( {{x^3}-2{x^2} + x - 1} \right)\left( {5-x} \right)} \hfill \cr
{ = - \left( { - {x^4} + 7{x^3}-11{x^2} + 6x - 5} \right)} \hfill \cr
{ = {x^4} - 7{x^3} + 11{x^2} - 6x + 5} \hfill \cr} \)
(Ở đây ta biến đổi: \(x - 5 = - (5 - x)\))
2. Giải bài 8 trang 8 SGK Toán 8 tập 1
Làm tính nhân
a) \(\left(x^2y^2 - \dfrac{1}{2}xy + 2y\right)(x - 2y)\)
b) \((x^2 - xy + y^2)(x + y)\)
Phương pháp giải
Áp dụng quy tắc nhân đa thức với đa thức: Muốn nhân một đa thức với một đa thức, ta nhân mỗi hạng tử của đa thức này với từng hạng tử của đa thức kia rồi cộng các tích với nhau.
Hướng dẫn giải
Câu a
\(\begin{array}{l} \left( {{x^2}{y^2} - xy + 2y} \right)\left( {x - 2y} \right)\\ = {x^2}{y^2}x + {x^2}{y^2}( - 2y) - xy.x - xy( - 2y) + 2y.x + 2y.( - 2y)\\ = {x^3}{y^2} - 2{x^2}{y^3} - {x^2}y + 2x{y^2} + 2xy - 4{y^2} \end{array}\)
Câu b
\(\begin{array}{*{20}{l}} \begin{array}{l} \left( {{x^2}-xy + {y^2}} \right)\left( {x + y} \right)\\ = {x^2}.x + {x^2}.y + \left( { - xy} \right).{\rm{ }}x + \left( { - xy} \right).{\rm{ }}y + {y^2}.{\rm{ }}x + {y^2}.y \end{array}\\ \begin{array}{l} = {x^3} + {x^2}.y - {x^2}.y - x{y^2} + x{y^2} + {y^{3\;}}\\ {\rm{ = }}{x^3} - {y^3} \end{array} \end{array}\)
3. Giải bài 9 trang 8 SGK Toán 8 tập 1
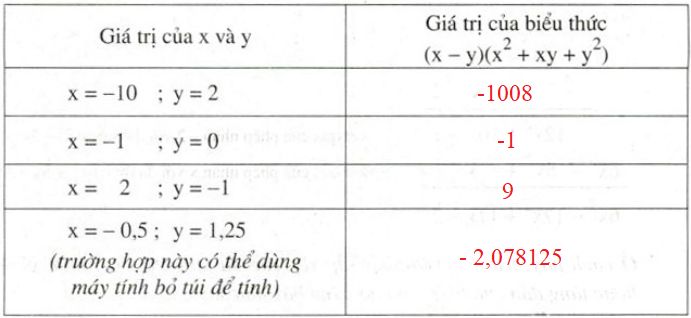
Điền kết quả tính được vào bảng

Phương pháp giải
- Áp dụng qui tắc nhân đa thức với đa thức để nhân phá ngoặc rồi rút gọn biểu thức.
- Thay giá trị \(x, y\) tương ứng để tính giá trị của biểu thức.
Hướng dẫn giải
Trước hết, ta làm tính nhân để rút gọn biểu thức, ta được
\({\left( {x - y} \right)\left( {{x^2} + xy + {y^2}} \right)}\)
\( = x\left( {{x^2} + xy + {y^2}} \right) - y\left( {{x^2} + xy + {y^2}} \right)\)
\( = x.{x^2} + x.xy + x.{y^2} + \left( { - y} \right).{x^2} \)\(+ \left( { - y} \right).xy + \left( { - y} \right).{y^2}\)
\( = {x^3} + {x^2}y + x{y^2}-y{x^2}-x{y^2}-{y^3} \)
\( = {x^3} + \left( {{x^2}y - y{x^2}} \right) + \left( {x{y^2} - x{y^2}} \right)\)\(\, - {y^3}\)
\(= {x^3}-{y^3}\)
Sau đó tính giá trị của biểu thức: \( A={x^3}-{y^3}\)
Ta có
Khi \(x = -10; y = 2\) thì \(A = {\left( { - 10} \right)^3}-{2^3} = - 1000-8 \)\(= - 1008\)
Khi \(x = -1; y = 0\) thì \(A = {\left( { - 1} \right)^3}-{0^3} = - 1\)
Khi \(x = 2; y = -1\) thì \(A = {2^3}-{\left( { - 1} \right)^3} = 8 + 1 = 9\)
Khi \(x = -0,5; y = 1,25\) thì
\(A = {\left( { - 0,5} \right)^3}-1,{25^3} \)\(= - 0,125-1,953125 = - 2,078125\)
4. Giải bài 10 trang 8 SGK Toán 8 tập 1
Thực hiện phép tính
a) \((x^2 - 2x + 3)\left(\dfrac{1}{2}x - 5\right)\)
b) \((x^2 - 2xy + y^2)(x - y)\)
Phương pháp giải
Áp dụng qui tắc nhân đa thức với đa thức để nhân phá ngoặc rồi rút gọn biểu thức.
Hướng dẫn giải
Câu a
\(\begin{array}{l} \left( {{x^2} - 2x + 3} \right)\left( {\frac{1}{2}x - 5} \right)\\ = \frac{1}{2}{x^3} - 5{x^2} - {x^2} + 10x + \frac{3}{2}x - 15\\ = \frac{1}{2}{x^3} - 6{x^2} + \frac{{23}}{2}x - 15 \end{array}\)
Câu b
\(\begin{array}{l} \left( {{x^2}-2xy + {y^2}} \right)\left( {x-y} \right)\\ \begin{array}{*{20}{l}} { = {x^3} - {x^2}y - 2{x^2}y + 2x{y^2} + x{y^2} - {y^3}}\\ { = {x^3} - 3{x^2}y + 3x{y^2} - {y^3}} \end{array} \end{array}\)
5. Giải bài 11 trang 8 SGK Toán 8 tập 1
Chứng minh rằng giá trị của biểu thức sau không phụ thuộc vào giá trị của biến: \( (x – 5)(2x + 3) – 2x(x – 3) + x + 7\)
Phương pháp giải
Áp dụng quy tắc nhân đa thức với đa thức để nhân phá ngoặc rồi rút gọn biểu thức, kết quả cuối cùng là hằng số thì giá trị của biểu thức không phụ thuộc vào biến.
Hướng dẫn giải
\(\begin{array}{*{20}{l}} {\left( {x - 5} \right)\left( {2x + 3} \right) - 2x\left( {x - 3} \right) + x + 7}\\ { = 2{x^2} + 3x - 10x-{\rm{ }}15-2{x^2} + 6x + x + 7}\\ \begin{array}{l} = 2{x^2}-2{x^2}-7x + 7x-15 + 7{\rm{ }}\\ = - 8 \end{array} \end{array}\)
Vậy sau khi rút gọn biểu thức ta được hằng số -8 nên giá trị biểu thức không phụ thuộc vào giá trị của biến.
6. Giải bài 12 trang 8 SGK Toán 8 tập 1
Tính giá trị của biểu thức \((x^2 - 5)(x + 3) + (x + 4)(x - x^2)\) trong mỗi trường hợp sau
a) \(x = 0 \)
b) \(x = 15 \)
c) \(x = -15 \)
d) \(x = 0,15\)
Phương pháp giải
- Áp dụng qui tắc nhân đa thức với đa thức để nhân phá ngoặc rồi rút gọn biểu thức.
- Thay giá trị của \(x\) vào biểu thức đã được rút gọn để tính giá trị của biểu thức.
Hướng dẫn giải
Trước hết thực hiện phép tính và rút gọn, ta được
\(\begin{array}{*{20}{l}} {\left( {{x^2}-5} \right)\left( {x + 3} \right) + \left( {x + 4} \right)\left( {x-{x^2}} \right)}\\ { = {x^3}+ 3{x^2} - 5x-15+{x^2}-{x^3}+4x-4{x^2}}\\ { = {x^3}-{x^3} + {4x^2}-4{x^{2\;}}-5x + 4x - 15}\\ { = - x - 15} \end{array}\)
Câu a: Với \(x = 0\) giá trị của biểu thức đã cho là: \(- 0 - 15 = -15\)
Câu b: Với \(x = 15\) giá trị của biểu thức đã cho là: \(- 15 - 15 = -30\)
Câu c: Với \(x = -15\) giá trị của biểu thức đã cho là: \(-(-15) - 15 = 15 -15 = 0\)
Câu d: Với \(x = 0,15\) giá trị của biểu thức đã cho là: \( -0,15 - 15 = -15,15.\)
7. Giải bài 13 trang 9 SGK Toán 8 tập 1
Tìm \(x,\) biết: \((12x -5)(4x - 1) + (3x - 7)(1 - 16x) = 81\)
Phương pháp giải
Áp dụng quy tắc nhân đa thức với đa thức để nhân phá ngoặc rồi rút gọn biểu thức, sau đó tìm \(x.\)
Hướng dẫn giải
Ta có: \((12x - 5)(4x - 1) + (3x - 7)(1 - 16x) = 81\)
\(\Leftrightarrow 48x^2 - 12x - 20x + 5 + 3x - 48x^2 - 7 + 112x = 81\)
\(\Leftrightarrow 83x - 2 = 81\)
\(\Leftrightarrow 83x = 83\)
\(\Rightarrow x = 1\)
8. Giải bài 14 trang 9 SGK Toán 8 tập 1
Tìm ba số tự nhiên chẵn liên tiếp, biết tích của hai số sau lớn hơn tích của hai số đầu là 192.
Phương pháp giải
- Hai số chẵn liên tiếp hơn kém nhau \(2\) đơn vị.
- Gọi ba số chẵn liên tiếp là \(a, a + 2, a + 4\); lập biểu thức biểu thị mối quan hệ giữa các ẩn.
- Thực hiện nhân đa thức với đa thức để rút gọn biểu thức rồi tìm giá trị của số chẵn bé nhất, sau đó tìm được hai số còn lại.
Hướng dẫn giải
Gọi ba số chẵn liên tiếp là \(a, a + 2, a + 4\) \(\left( {a \text{ là số chẵn};a \in\mathbb N} \right)\)
Tích hai số sau là: \((a + 2)(a + 4)\)
Tích hai số đầu là: \(a(a + 2)\)
Theo đề bài tích của hai số sau lớn hơn tích của hai số đầu là \(192\) nên ta có:
\((a + 2)(a + 4) - a(a + 2) = 192\)
\(a\left( {a + 4} \right) + 2\left( {a + 4} \right) - a\left( {a + 2} \right) = 192\)
\(a.a + a.4 + 2.a + 2.4 + ( - a).a + ( - a).2 = 192\)
\({a^2} + 4a + 2a + 8 - {a^2} - 2a = 192\)
\(\left( {{a^2} - {a^2}} \right) + \left( {4a + 2a - 2a} \right) = 192 - 8\)
\(4a= 184\)
\(a=184:4\)
\(a = 46\) (thỏa mãn điều kiện)
Vậy ba số đó là \(46, 48, 50.\)
9. Giải bài 15 trang 9 SGK Toán 8 tập 1
Làm tính nhân
a) \(\left(\dfrac{1}{2}x + y\right)\left(\dfrac{1}{2}x + y\right)\)
b) \(\left(x -\dfrac{1}{2} y\right)\left(x -\dfrac{1}{2} y\right)\)
Phương pháp giải
Áp dụng qui tắc nhân đa thức với đa thức để nhân phá ngoặc rồi rút gọn biểu thức.
Hướng dẫn giải
Câu a
(\begin{array}{l} (\frac{1}{2}x + y)(\frac{1}{2}x + y){\rm{ }}\\ = \frac{1}{2}x.\frac{1}{2}x + \frac{1}{2}x.y + y.\frac{1}{2}x + y.y\;\;\;\;\;\;\;\;\;\\ = \frac{1}{4}{x^2} + \frac{1}{2}xy + \frac{1}{2}xy + {y^2}\;\;\;\;\;\;\;\;\;\;\;\;\;\\ = \frac{1}{4}{x^2} + xy + {y^2}\;\\ \end{array}\)
Câu b
\(\begin{array}{l} (x - \;\frac{1}{2}y)(x - \;\frac{1}{2}y){\rm{ }}\\ = x.x + x( - \frac{1}{2}y) + ( - \frac{1}{2}y.x) + ( - \frac{1}{2}y)( - \frac{1}{2}y)\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{ }}\\ = {x^2} - \frac{1}{2}\;xy{\rm{ }} - \frac{1}{2}\;xy{\rm{ }} + \;\frac{1}{4}\;{y^2}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{ }}\\ = {x^2} - xy + \;\frac{1}{4}{y^2}\\ \end{array}\)
Tham khảo thêm
- doc Giải bài tập SGK Toán 8 Bài 1: Nhân đơn thức với đa thức
- doc Giải bài tập SGK Toán 8 Bài 3: Những hằng đẳng thức đáng nhớ
- doc Giải bài tập SGK Toán 8 Bài 4: Những hằng đẳng thức đáng nhớ (tiếp theo)
- doc Giải bài tập SGK Toán 8 Bài 5: Những hằng đẳng thức đáng nhớ (tiếp theo)
- doc Giải bài tập SGK Toán 8 Bài 6: Phân tích đa thức thành nhân tử bằng phương pháp đặt nhân tử chung
- doc Giải bài tập SGK Toán 8 Bài 7: Phân tích đa thức thành nhân tử bằng phương pháp dùng hằng đẳng thức
- doc Giải bài tập SGK Toán 8 Bài 8: Phân tích đa thức thành nhân tử bằng phương pháp nhóm hạng tử
- doc Giải bài tập SGK Toán 8 Bài 9: Phân tích đa thức thành nhân tử bằng cách phối hợp nhiều phương pháp
- doc Giải bài tập SGK Toán 8 Bài 10: Chia đơn thức cho đơn thức
- doc Giải bài tập SGK Toán 8 Bài 11: Chia đa thức cho đơn thức
- doc Giải bài tập SGK Toán 8 Bài 12: Chia đa thức một biến đã sắp xếp



